1. 概要
生体分子のある特定部分の原子・補欠分子等に由来する様々な分光スペクトルを解析して生体分子の構造・機能相関を議論する「分光測定法」が広く使われている。そのなかで、電子常磁性共鳴法は奇数個の電子(不対電子)を持つ常磁性分子、イオンをその測定対象とする。電子常磁性共鳴は EPR と略記する。電子スピン共鳴 ESR として親しまれているが、広く常磁性分子を対象とするので EPR という呼称の方が適切である。生体試料中では遊離基(ラジカル)と常磁性金属イオンにその対象が限られる。この手法は検出感度が高く、固有の信号を与えるので、いくつかの常磁性分子種が混ざり合った系を取り扱う場合でも非破壊的に試料中に含まれる常磁性分子種の区別、同定、定量が可能になる。従って、生体物質を研究する理想的な実験法のひとつである。金属タンパク質、とりわけヘムタンパク質の研究において、EPR は金属をプローブとして活性中心金属の原子価、錯体の対称性、配位子との結合状態、あるいは電子状態など X 線結晶構造解析では得られないミクロ分子環境の精密な知見を提供する。すなわち、金属タンパク質の構造と機能を追究する重要な測定手段になる。本稿では、多くの研究室で使用されている普通の EPR 装置を使って、金属タンパク質とりわけヘムタンパク質を測定する際の基本的な実験技術、注意事項、裏ワザなどを紹介する。
2. はじめに
2-1 EPR の原理
詳しくは参考文献(1–3)等を参照されたい。一個の電子(不対電子:スピン量子数 \(S = 1/2\))を考えると、電子自身は自転運動をしているので磁気モーメント(小さい磁石と考えてよい)を持っている。外部から磁場 \(\boldsymbol{B}\) を加えると磁気モーメントは磁場の方向を向いて歳差運動するものと、反対方向に向いて歳差運動するものとに分かれる。即ち、縮退していた電子スピンのエネルギー準位が分裂する。
2-1-1 \(\boldsymbol{g}\) 値
縮退していたエネルギー準位が磁場によって分裂する現象を「ゼーマン分裂」という。
エネルギー差 \(\Delta E\) を\(g \beta B\) で表す(\(\beta\) は Bohr 磁子で \(9.274 \times 10^{-24}{\ }\mathrm{J/T}\))。\(\Delta E\) に相当するマイクロ波(周波数 \(\nu\) のマイクロ波のエネルギーは \(h \nu\)、\(h\) はプランク定数で \(6.626 \times 10^{-34}{\ }\mathrm{J} \cdot \mathrm{s}\))の共鳴吸収現象が EPR である。ここで重要なのは、\(g\) 値と呼ばれる比例定数である。\(g\) 値は不対電子の置かれている環境に依存する物質固有の物理量で、外部磁場 \(B\)、マイクロ波周波数 \(\nu\) との間には
\[g = 0.71449 \times \nu^{\mathrm{[MHz]}} / 10B ^{\mathrm{[mT]}} \tag*{[1]}\]の関係がある。ここで、T(テスラ)は磁場の単位で、1 T は10,000ガウスに相当する。ここでは、\(g\) 値とは EPR 信号の現れる場所を示すものと思えばよい。
2-1-2 吸収と緩和
定常状態の EPR 信号が観測されるためには、共鳴条件を満足するマイクロ波を吸収して高いエネルギー準位に上がったスピンがエネルギーを他のスピン系に与えて低いエネルギー準位に落ち(緩和現象)、再びマイクロ波を吸収する過程がひき続いて起こらなければならない。磁気共鳴の現象は Bloch 方程式によって説明される(1,2)。EPR は吸収現象であると同時に緩和現象でもある!
2-1-3 超微細構造(hfs)
電子スピン(\(S\))が核スピン(\(I\))を持つ核の磁気モーメントと相互作用すると EPR 信号は \(2I + 1\) 本に分裂する(核スピン量子数 \(\boldsymbol{I}\) が量子化されると \(I_{\mathrm{z}}\) は \(- | I |\) から \(+ | I |\) まで \(2I + 1\) とおりの状態をとる。電子スピンは \(2I + 1\) とおりの核スピンによる局所磁場を感じて、EPR 信号が \(2I + 1\) 本に分裂する)。これが超微細構造(hfs)といわれるものである。超微細構造を観測することで、不対電子と相互作用する周辺原子の核種の同定や電子スピンの局在環境の解析ができる。
2-2 どんな EPR 装置を使うか
重要なキーワードについて少し触れておこう (4, 5)。
2-2-1 CW-EPR 法とパルス EPR 法
EPR スペクトルを定常的に観測するには、マイクロ波周波数を一定にして磁場を掃引する CW-EPR 法(連続波 EPR 法)が一般的である。これに対して初めから共鳴条件を満たす外部磁場下で強力なマイクロ波パルス磁場を与え、マイクロ波パルス磁場が切れたのちのスピンの挙動を解析するパルス EPR 法が近年盛んに行なわれるようになってきた。パルス EPR 法は素晴らしい技術であるが、気楽に生体試料測定に利用されるに至っていないのが現状であろう。まだまだ 10 GHz(X 帯)を中心とした CW-EPR 法でやれることも多い。パルス EPR 測定をする場合でも、その基礎として CW-EPR の原理と測定理論の理解が必要である。本稿では多くの研究室で利用されている CW-EPR 法を中心に話を進める。
2-2-2 使用するマイクロ波周波数帯
一般には X 帯(10 GHz)の EPR 装置が普及している。10 GHz 帯以外では、L(1 GHz)、S(3 GHz)、K(24 GHz)、Q(35 GHz)、W(92 GHz)帯の EPR 装置が市販されている。Q 帯の EPR 測定までは通常の電磁石が使用されるが、W 帯の EPR 装置の磁場発生は超伝導磁石が必要である。上記の周波数帯以外での EPR 測定は自作の装置に依らなければならない。近年、高周波数・強磁場 EPR 測定が盛んに行なわれるようになってきた (6–8)。
- 通常の EPR 測定では、マイクロ波エネルギーを効率よく溜め込んだ「空洞共振器」とよばれる箱の中に試料を挿入する。空洞共振器の大きさ(体積)は使用するマイクロ波の周波数に依存する。
- マイクロ波周波数を高くすると空洞共振器の体積は小さくなるので、空洞共振器における試料の充填率の関係で使用試料体積を少なくできる利点がある。
- \(g\) 値は式 \([1]\) で示したようにマイクロ波周波数に比例するので、異方性 \(g\) 値(後述)の分離を高めるには高周波数帯の EPR が向いている。
- 不対電子が核スピンと相互作用して hfs 分裂を示す場合には、分裂が磁場に依らないため、X 帯以外に低周波数帯(例えば L 帯)EPR による観測を行うことで、\(g\) 値の異方性か hfs 分裂かの区別がつく(hfs 分裂が磁場に依存しない場合)。
- マイクロ波周波数カウンターは EPR 装置に内蔵されているが、付いていない場合は外部出力端子からマイクロ波の一部を取り出し、別途用意した周波数カウンターに接続する。導波管の途中に周波数メーター(周波数測定のために周波数較正された空洞共振器)を挿入して Q-ディップ(後述)位置での周波数を読み取る方法もある。あるいは、標準試料 DPPH(1,1-diphenyl-2-picrylhydrazyl)の EPR 信号(\(g = 2.0036\))位置の磁場を測定すれば周波数が決められる。
- 正確な磁場はプロトン NMR(核磁気共鳴)磁場測定器により求める。永年使用していると、EPR 装置が示す磁場表示はズレてくる。プロトン NMR で時々較正する必要がある。
2-2-3 基礎知識として知っておきたいこと
EPR 装置の操作手順は製造各社によって若干異なるが、最近の装置は全てコンピューターで制御されているのでマニュアルに従えば、だれでも簡単に測定はできる。EPR スペクトルを測定する上で知っていなければならない基礎について簡単に記しておく。図1に EPR 測定装置の概略図を示す。電源や電磁石には高電流が流れるので発熱する。そのため、先ず冷却装置で装置を冷やす必要がある。次に、マイクロ波が発信すると発振モードがディスプレー上に現れる。
① モードチェック
マイクロ波の発振にはガンダイオードが使用されている。発振周波数を変えるためにバラクターダイオードが組み込まれている。ガンダイオードの電圧を変えても発振周波数はあまり変化しないが、バラクターダイオードの電圧を変化させると発振周波数が変わる。したがって、バラクターダイオードの直流電源に変調電圧(低周波交流電圧)を印加することによってマイクロ波の発振状態をオッシロスコープ上で観測できる。これが発振モードである。一部の装置では、クライストロンという真空管でマイクロ波を発振させているものがある。ガンダイオードより発振帯域が広く、発振出力も大きくとれるが、高電圧電源を使う。バリアン社製の EPR は既に製造していないので、クライストロンの入手は困難である。中古品か代替品を探すことになる。
発振モードの中央に空洞共振器の Q-ディップが現れる(図2)。Q-ディップとは空洞共振器にマイクロ波エネルギーが蓄えられている状態を示す。次に、試料を空洞共振器の中に入れて Q-ディップをみる。このとき、Q-ディップが鋭くなるように試料挿入位置を調整することで、マイクロ波磁界の最も密な位置(空洞共振器の中心部)に挿入できる。
メモ
② AFC(自動周波数制御)
CW-EPR では一般にマイクロ波周波数を固定する必要がある。AFC とよばれる自動周波数制御装置で Q-ディップ中心のマイクロ波周波数を固定する。ここまでは大抵の EPR 装置は自動でやってくれる。本稿では AFC の動作原理についてふれないので、参考実験書を参考にされたい (5)。
③ 磁場変調
外部掃引磁場に小さい振幅の変調磁場を加え、その周波数成分を位相敏感検波器(PSD)で検出することによって EPR 信号の感度を向上させている(雑音信号の低減)。結果として、測定される EPR スペクトルは磁場の一次微分曲線になる。
- 変調磁場の振幅を小さくすると信号強度は減少し、大き過ぎると微分曲線が変形する(ピーク間隔が拡がる)。限界をみつけるには変調磁場振幅を小さい方から徐々に大きくしていって、微分曲線のピーク間幅がずれ始めるところを目安とする。特に、EPR スペクトルに hfs による分裂がある場合は、変調幅を小さくとる必要がある。変調振幅が大き過ぎると hfs 分裂がつぶれてしまう結果になる。
- 変調磁場の変調周波数として、通常の装置では 100 kHz を用いることが多い。一般に低周波数の変調磁場より高周波数の変調磁場の方が S/N 比は向上する。
メモ
④ 飽和現象
定常状態のEPRスペクトルに関して、少しふれておく。互いに相互作用のない \(N\) 個の電子スピン量子数 \(S = 1/2\) の常磁性分子を考える。磁場 \(B_{0}\) 中では、それぞれの電子スピンが \(E_{+}\)(\(S_{z} = +1/2\))、\(E_{-}\)(\(S_{z} = -1/2\))に対応したゼーマン分裂をし、ある温度 \(T\) でそれぞれ \(N_{+}\)、\(N_{-}\) のスピンが分布して平衡に達しているものとする。ここで、スピン総数を \(N = N_{-} + N_{+}\) とし、\(E_{-}\) と \(E_{+}\) 準位のスピン数の差を \(n = N_{-} - N_{+}\) とする。スピン数の差 \(n\) は信号強度に比例する。
このような系に周波数 \(\nu\) のマイクロ波が照射され、磁場 B0 が共鳴条件を満たせば、\(E_{-}\) 準位にある電子が電磁波を吸収して \(E_{+}\) 準位に、また \(E_{+}\) 準位の電子は電磁波を放射して \(E_{-}\) 準位に遷移する。この両遷移確率 \(W\) は等しいので、マイクロ波の正味の吸収は \(N_{-}\) と \(N_{+}\) の差によって決まる。従って、\(n(t)\) の時間変化は \(n_{0} \mathrm{e}^{-2Wt}\) となる。ここで、\(n_{0}\) は \(t = 0\) での \(E_{-}\) と\(E_{+}\) 準位のスピン数の差である。\(t \rightarrow \infty\) では \(E_{-}\) と \(E{+}\) におけるスピン数が等しくなり(\(n(t) \rightarrow 0\))、EPR 吸収が起こらなくなることを意味する。これがいわゆる「飽和」である。
しかし、現実の系では、観測された EPR 信号がマイクロ波照射時間とともに減少することはない。事実、励起された電子は \(T_{1}\) という寿命で外部にエネルギーを放出して元の準位に戻る「緩和過程」が必要になる。この緩和過程を理解するには、共鳴条件を満たすマイクロ波の照射を停止して \(n(t)\) の時間変化がどうなるかをみるのが分かり易い。平衡分布を回復しようとする速さは平衡からのずれ \(n_{0} - n\) に比例するから、\(n(t) = n_{0} \left( 1 - \mathrm{e}^{-t/T_{1}} \right)\) で表わされる。時間 \(t\) が十分に経てば、分布は平衡分布 \(n_{0}\) に戻ることを示している。ここで、\(T_{1}\) はスピン – 格子緩和時間といい、平衡分布に戻るまでの時間である。\(T_{1}\) が短いということは、スピンと他の自由度との結合が強い事を意味している。
現実には、前述したように、共鳴条件を満足するマイクロ波を吸収して高いエネルギー準位に上がったスピンがエネルギーを他のスピン系に与えて低いエネルギー準位に落ち、再びマイクロ波を吸収する過程がひき続いて起こらなければならない。マイクロ波吸収による平衡からのずれと緩和による平衡への回復との競り合いで \(n(t)\) の時間変化は \(\dfrac{dn}{dt} = -2W \cdot n + \dfrac{n_{0} - n}{T_{1}}\) と記述できる。これを定常状態(\(dn/dt = 0\))で解くと、\(n = \dfrac{n_{0}}{1 + 2WT_{1}}\) が得られる (2)。\(WT_{1} \ll 1\) ならば、\(n \sim n_{0}\) となるので、振動磁場からエネルギーを吸収しても、占有数 \(n\) は平衡値 \(n_{0}\) から大きくずれることはない。一方、\(W\) が十分大きくなると、\(n\) が次第に小さくなることがわかる。これが「飽和」である。EPR で観測される信号強度は \(nB_{1}\) に比例する (5)。ここで、\(B_{1}\) は入射マイクロ波の振動磁場である。また、遷移確率 \(W\) には振動磁場 \(B_{1}\) の2乗の項が含まれているので、EPR 信号強度は \(\dfrac{B_{1}}{1 + {aB_{1}}^{2}T_{1}}\) に比例することになる(\(a\) は吸収の線形を表す因子である)。\(B_{1}\) が小さく、\({aB_{1}}^{2}T_{1} \ll 1\) の範囲では、信号強度は\(B_{1}\) に比例して増加することを示している。\(B_{1}\) は \(\sqrt{P\text{(マイクロ波の出力)}}\) に比例するので、信号強度は \(\sqrt{P}\) に比例する。他方、\(B_{1}\) が増加して、\({aB_{1}}^{2}T_{1} \gg 1\) の程度になると、信号強度は \(1/B_{1}\) に比例する。\(B_{1}\) の増加につれて信号強度が減少し、飽和が観測される。したがって、飽和を防ぐために、普通の実験では低出力のマイクロ波磁場が用いられている。
適切なマイクロ波出力で、正しく EPR スペクトルを観測するにはEPRの信号強度(\(I\))と使用マイクロ波出力(\(P\))の関係を調べ、グラフより判断する方法を図3に示す。
例えば、マイクロ波出力を大きくすると飽和する分子種 A とマイクロ波出力を大きくしても飽和し難い分子種 B が混在する系を考えてみる。マイクロ波出力を大きくすると A 分子は飽和して信号強度は低下するが、B 分子は飽和しないので信号強度が増大する。従って、飽和現象を利用することで、A、B 分子種の信号を区別することが可能になる。
また、\(T_{1}\) が長くなるとスピンを通してマイクロ波から吸収されたエネルギーが他の自由度に流れていく速度が遅くなり、平衡分布に戻そうとする傾向が弱くなる。緩和が遅れると EPR 信号強度が減少する。
⑤ 吸収線の形と線幅
共鳴吸収は \([1]\) 式で与えられる共鳴磁場のところで観測されるだけでなく、その前後のある範囲にわたって観測され、線幅をもっている。不確定性原理によれば、時間の不確定さ \(\Delta t\) とエネルギー準位の不確定さ \(\Delta E\) の間には \(\Delta E \cdot \Delta t \sim h\) の関係がある。励起されたスピンの寿命はスピン系とその周辺との相互作用などによって有限であるとすれば(\(\Delta t = T_{1}\))、スピンのエネルギー準位には \(\Delta E\) の不確定さが生ずることになる。これがスペクトルの線幅になって表れる。スペクトルの線幅は、大ざっぱに \(1/T_{1}\) の程度である。このように、スペクトルの線幅はスピン系とその周辺との相互作用の強さと緩和時間に依存することになる。緩和時間が短いと線幅が広くなることがわかる。
- 電子スピン緩和が Bloch 方程式によって記述される場合にはローレンツ型によって線形を表すことができる。緩和がスピン–格子相互作用で規制され、共鳴点をゆっくりと通過する系(スピン系が熱的平衡を保つように分布している均一なスピン系)に対して Bloch 方程式を解くと、マイクロ波磁場 \(B_{1}\) と90°位相のずれたローレンツ型吸収信号と、\(B_{1}\) と同位相の分散信号が得られる。溶液で観測される EPR の線形はローレンツ型に近い。
- 電子スピンと電子スピン、または電子スピンと核スピンとの間の双極子相互作用が生じると、ローレンツ型曲線とは異なった線形になる。不均一なスピン系では個々の不対電子はそれぞれ異なった局所磁場を受けて、共鳴磁場にずれが生ずる。このような共鳴磁場のずれによる吸収線の拡がりは、局所磁場の分布を表している。統計理論に従えば、この分布はガウス分布とみなしてよい。スピン–スピン相互作用の過程が格子への緩和に比べて十分ゆっくりしているのなら、スピン系は熱的平衡に達せず、吸収線はガウス型になることが導かれる。固体試料で観測される EPR の線形はローレンツ型、またはガウス型のいずれかによって近似的に表される。
- 得られた EPR 吸収線の線形がローレンツ型かガウス型かを区別するには、微分傾斜法あるいは、吸収曲線の半値幅と最大傾斜幅の比によって判断することができる(図4)。
⑥ スピン濃度の定量化
測定した EPR 吸収の面積はスピン濃度(不対電子の数)に比例する。この面積は、一次微分 EPR スペクトルを二回積分して求める(図5)。スピン濃度が既知である標準試料と濃度未知の試料を、それぞれ等しい測定条件に設定して(マイクロ波飽和等のない条件)測定する。それぞれの EPR スペクトルの二回積分値よりスピン濃度の相対的な定量ができる。同一分子間でのスピン濃度の相対比較は、単純に EPR 吸収強度の比で求まる。
3. 最適な条件で EPR 測定をするために
ここまで述べてきたことを基礎として、実際に金属タンパク質の EPR 測定を行うにあたって何が問題になるか、その時どうするかについて述べる。
3-1 EPR 活性な金属イオン
酵素、タンパク質の多くは、なんらかの形で \(\ce{Na}\)、\(\ce{K}\)、\(\ce{Mg}\)、\(\ce{Mn}\)、\(\ce{Fe}\)、\(\ce{Co}\)、\(\ce{Ni}\)、\(\ce{Cu}\)、\(\ce{Zn}\)、\(\ce{Se}\)、\(\ce{Mo}\) などの金属イオンを必要として生命現象の調節を行っている。EPR で観測可能な \(3d\) 遷移金属イオンを表1に示す。本稿では、これらの \(3d\) 遷移金属イオンを含むタンパク質、特に鉄錯体であるヘムを含むヘムタンパク質やヘム鉄をこれら遷移金属で置換したヘムタンパク質の EPR 測定を中心に話を進める。
3-2 溶液試料の測定
EPR では溶液または単結晶の試料標品が測定の対象になる。先ず、溶液試料で、測定温度が室温の場合と低温(凍結試料)の場合について述べる。
3-2-1 室温での測定
金属イオンの不対電子は緩和時間が短いものが多く、室温での EPR 観測は難しい。従って、大抵の場合は(極)低温での測定となる。室温で EPR 測定が可能になる金属タンパク質は限られる(表1参照)。金属タンパク質以外の測定でも、安定なラジカル試薬を標識としてタンパク質の特定部位のアミノ酸残基に直接化学結合させるスピンラベル法では、ラジカル分子の EPR スペクトルから標識部位周辺の環境や運動状態を探るので、当然EPR測定は室温である。
室温での測定において緩和時間以外で特に問題になるのは、生体試料中の水分子の存在である。水がマイクロ波を吸収するので(誘電損失)、空洞共振器に蓄えられるマイクロ波のエネルギーが減少し、Q-ディップの Q 値の低下が起こる。極端な場合は Q-ディップが観測できなくなる。このような場合には、ループギャップ共振器を使う方法もある (9)。S/N 比は格段に向上するが、ここでは省略する。一般には、誘電損失を抑えるために、試料体積を小さくするための工夫がなされる。
メモ
① 細管型セルを用いる場合
石英製試料管の内径を出来るだけ小さくし(内径 0.8 mm φ 程度)、試料体積を減らす。10 μL を目安として、Q-ディップの状態をみながら試料量を調節するとよい。この場合、細い試料管は折れ易いので、試料管のホルダーとして外径 4~5 mm φ の通常の EPR 試料管に挿入して測定するとよい。
更に、このEPR試料管を後述する低温測定用の挿入型石英製デュワー瓶に挿入して(室温で)測定すると信号強度は増大する。あるいは、石英細管の外径は大きい方がよい結果が得られる(外径 4 mm φ、内径 0.8 mm φ 程度の肉厚石英試料管が一般的)。これは、空洞共振器中心部に挿入されている石英管部分にマイクロ波磁界が集るので、試料位置での信号強度増大がみられるためである。このような工夫は、マイクロ波飽和のない試料には有効であろう。
② 扁平型セルを用いる場合
これに対して、石英製の扁平型試料管を用いると Q 値を低下させることなく試料体積も 50~90 μL 程度に増やすことができるが、扁平試料管が空洞共振器内でマイクロ波電界を横切らないように挿入しなければならない。特に TE102 矩形型空洞共振器では注意を要する。
③ 空洞共振器内の温度制御
測定中はマイクロ波によって試料の温度が上昇するので、AFC によるマイクロ波周波数制御が外れ易くなる。乾燥空気または乾燥窒素ガスを空洞共振器内に常に流す必要がある。温度制御された特別なフローデュワー装置を用いるのが最良である。
3-2-2 極低温での測定
多くの金属タンパク質の金属イオンの緩和時間は室温では短いため、スペクトルの線幅増大が起こり、EPR 観測ができないことが多い。緩和時間は温度依存性を示し、極低温にすると一般に長くなるので、吸収の線幅が狭くなり EPR 信号の観測が可能になる。また、短寿命の酵素反応中間体分子種を室温の EPR で観測することは難しい。従って、極低温(液体窒素温度以下)で反応中間体を安定に凍結捕捉し、低温下で EPR を観測することが必要になる。以上の理由で、金属タンパク質の EPR 測定は極低温で行うことが一般的である。凍結補足のための特別な装置については後で述べる。
メモ
① 有効試料体積
通常の 10 GHz 帯 EPR で使用する薄肉石英製 EPR 試料管(スプラジル Suprasil 石英試料管)の外径は 4~5 mm φ で、有効試料量は 50~150 μL である。使用できる有効試料量は使用する空洞共振器のモードによっても異なる。TE102 矩形型空洞共振器では精々 150 μL 程度だが、TE011 円筒型空洞共振器ではこの倍以上の試料量までは可能である。試料の量は装置自体の感度、測定試料の濃度や貴重度(精製の困難さなど)を考慮して決めればよい。
メモ
②液体窒素温度(77 K)での測定について
液体窒素温度(77 K)での EPR 測定ではフィンガータイプの石英製デュワー瓶を空洞共振器内に挿入して用いるのが一般的である(空洞共振器への挿入部の外径 11 mm φ)。デュワー瓶内で、液体窒素の自然気化による窒素ガスの気泡が空洞共振器のQ値を不規則に変化させてノイズを発生させるため、測定には苦労することが多い。
古来、このノイズを抑える工夫がなされてきた。完全に窒素の気泡を止めても、スペクトル積算などで長時間測定し続けると、窒素の気泡が突然発生して AFC が外れてしまい、泣かされることがある。むしろ、連続した小さな気泡をデュワー底部から発生させると(少々 S/N 比を犠牲にしてでも)AFC が外れるとか、スパイク状ノイズが発生するなどの事故は抑えられる。
- 小さな気泡をデュワー底部から発生させるには、EPR 試料管をデュワー瓶の低部に触れるように置くだけでよい。EPR 試料管上部をティシュペーパーなどで軽く捲いてデュワー瓶の開口上部に軽く固定する。この場合、スペクトルは数回積算すれば S/N 比は改善する。
- それでも S/N 比が気になる場合は、−190℃~室温まで温度制御できるフロー型クライオスタットを使用する。この温度制御装置は、液体窒素の蒸発量とヒーターを加減して、窒素ガス流量を調節して試料部分の温度を制御するもので、EPR 装置製造各社が其々の空洞共振器のクライオスタット挿入口のネジピッチに合わせた製品を販売している(液体窒素以外に、47 m3 程度の窒素ガスボンベが必要である)。極低温での測定では空洞共振器内の石英製デュワー外壁に水滴が付くので(Q 値が低下する)、フィルターを通した乾燥空気か窒素ガスをゆっくりと空洞共振器内に流す必要がある。
- デュワー瓶の真空度が悪くなるとデュワー瓶外壁に水滴が付き易くなる。その時はデュワー瓶の真空引きを専門業者に依頼する必要がある。デュワー内壁のメッキが剥がれてデュワー先端の試料測定部(透明石英部分)に付着しないよう、細心の注意を依頼する。
③ 極低温での温度可変測定
ヘムタンパク質の EPR 測定では液体窒素温度以外に液体ヘリウム温度をはじめ様々な極低温温度が要求される。ひと昔前、筆者が学生の頃は液体窒素(77 K)、液体水素(20 K)と液体ヘリウム(4.2 K)の3定点測定が主であった。液体水素温度での測定では、液体窒素温度測定と同様にフィンガータイプの挿入型デュワーを利用した。この場合、液体窒素より細かい気泡が常時発生するため、ノイズの少ないスペクトルが得られる。しかし、危険物取扱上の問題があるため使用されなくなった。液体ヘリウム温度の場合は、空洞共振器ごとガラス製の二重デュワー(内側のデュワーに液体ヘリウムを満たし、外側のデュワーには液体窒素を入れる)に浸けて測定するため、簡単に試料の交換ができない問題があった。その後、空洞共振器に挿入できる液体窒素デュワーに液体ヘリウムの入った細いデュワーを挿入した二重構造デュワーが考案され、簡便に 4.2 K 定点での EPR 測定が行えるようになった。現在では、オックスフォード社製の液体ヘリウムのフロー型クライオスタットが広く一般に使用され、必要な測定温度を設定する事が容易になった。
フロー型クライオスタットについては使用マニュアルを熟読して馴れることに尽きる。
④ EPR 試料管に試料を入れるコツ
フロー型クライオスタットや挿入型デュワー瓶を使って EPR 測定をする場合、使用する EPR 試料管の長さは 20 cm を超える。試料標品を無駄なく EPR 試料管の底部に導入するためには、ポリエチレンチューブで作製した自在型ピペットを使用すると便利である(図6)。
EPR 試料管の上部は必ずゴムキャップなどでしっかりと封じてから試料を凍結する必要がある。これをしないと、液体窒素温度以下では空気中の酸素(三重項酸素なので常磁性分子であることに注意)が試料と共に試料管の底に溜り幅広い信号を出すため、試料の EPR 信号の邪魔になる。そのため、ゴムキャップで封じた後に、できれば試料管内部を窒素ガスに交換することも薦める。
⑤ 溶液試料を凍結させるときの注意
開口すれすれまで液体窒素を満たした(500 mL 程度の)金属製デュワー瓶に EPR 試料管を最下部から少しずつ挿入して凍結させる(試料を下の方から徐々に凍結させる)。試料の入っている試料管を一気に液体窒素に挿入した場合や、液体窒素が十分入っていないデュワー瓶内に挿入した場合は試料管が割れやすい。これは、試料上部が先に凍結することで、凍結時の体積膨張の逃がし口が無くなり、試料管の管壁方向に圧力がかかるためである。
- 貴重な試料の入っている試料管が割れた場合は慌てずに液体窒素デュワー瓶の中から試料を石英ガラスの破片ごとピンセットで拾い出し、マイクロチューブに回収する。試料を直ちに解凍し、ガラス破片を遠心分離後、上澄みを回収して EPR 試料管に入れ直す。
⑥ オックスフォード社のフロー型クライオスタットに試料管を挿入するときの注意
上記の手法で試料を凍結し、試料管の先端にヒビ割れがないことを確認して試料挿入口から試料管を挿入する。
- ヒビ割れがあるとクライオスタット内部で試料管が欠落することがある。その場合は、クライオスタットを取り外さなければならず、実験時間を無駄にすることになる。
- EPR 試料管の上部のゴムキャップの締めが緩いと、極低温での測定時に試料管内に空気が吸い込まれ固体化する。固化した空気は、試料管をクライオスタットから引き出す際に急激に気化するので試料管がロケットのように吹き飛んでしまうことがある(貴重な試料標品の回収ができなくなる!)。
- 試料管挿入口の位置固定締め具を強く締め過ぎると、EPR 試料管が折れることが偶にある。このときは、挿入口上部の試料管固定具ごと割れた試料管をそっと外し、試料管を回収する。もし運悪く試料管がクライオスタット内に落下している場合は、試料管の内径より少し小さい外径のアクリル丸棒などを試料管内に差し込んでゆっくり引き上げる。この操作はクライオスタット内のフローが停止していることを確認してから行う。
⑦ 試料凍結時に pH が変化する
溶液試料の pH は、凍結する際に変化する危険性がある。そのため、温度による pH 変化の少ない緩衝液を選択すべきである。このような溶液として、Good’s 緩衝液などが挙げられる。リン酸緩衝液では2種類のリン酸塩の溶解度が温度により異なる。\(\ce{KH2PO4}\)-\(\ce{Na2HPO4}\) 系では約 2pH 低下するとの報告がある (10)。また、同じ pH 値を示す緩衝液でも、ヘムタンパク質のヘム鉄に影響を与え EPR スペクトルが変化する場合もあるため、緩衝剤の選択には注意すべきである。pH の変化は凍結速度にも依存し、急速に凍結させた場合の変化は少ない。一気に試料を凍らせるには、液体窒素よりイソペンタン(2-メチルブタン)寒剤を用いる方法が優れている。
- イソペンタン寒剤を作るには、イソペンタン(100 mL 程度)を金属製デュワー瓶に入れ、−100℃程度になるまで、マグネチックスターラーで攪拌しながら液体窒素を少しずつ加えてゆく。温度確認のために、低温用の温度センサー挿入型デジタル温度計を用いるとよい。
- この寒剤の中に素早く EPR 試料管を投入すると、試料は瞬時に凍結する。試料管の周りに付着したイソペンタン寒材はティシュペーパーなどで良く拭き取ってから液体窒素のデュワー瓶に移して EPR 測定に備える。
メモ
⑧ 凍結試料を解凍するときの注意
EPR 測定が終わった後、試料管内の凍結試料を解凍して回収しなければならない。しかし、凍結試料の入っている試料管を室温で放置すると石英試料管が割れることがある。
- 液体窒素デュワー瓶から取り出した試料管の凍結試料部分全体に水道水をかけ続ける。素早く解凍することによって試料管の破損を防ぐと共に、pH 変化による試料の変性を防ぐことは重要である。
⑨ EPR 試料管の洗浄
はじめに、ポリエチレンチューブで作製した自在型ピペットを用いて試料管内の試料を回収する。次に、細管用洗浄ブラシに洗剤をつけて試料管内部の汚れを擦り落とす。(EPR 試料管の外側の汚れを除くことも忘れない!さらに、試料管の上部より洗浄瓶で脱イオン水を注入しながら、アスピレーターに接続した自在ピペットを使って試料管内を吸引洗浄する。洗剤等が残らないように注意する。十分に洗浄した後、試料管内の水分を出来るだけ除去(アスピレーターで吸い取るか、窒素ガスをゆっくりと流せば良い)し、乾燥器(100℃)に入れて乾燥させる。
- 試料管の洗浄度を確認するために、時々、試料管をガスバーナー/酸素で(石英管が曲がらない程度の温度で)焼くとよい。このとき、高温度炎中の試料管先端が透明なオレンジ色になれば、試料管は問題ない。しかし、濁った赤褐色のときは汚れがとれていないので、ガスバーナー/酸素の温度を高くして試料管先端の汚れている部分を焼き切り、先端を封じて整形する。
3-2-3 嫌気状態での EPR 測定
測定したい生体試料が酸素分子と反応させたくない場合、測定試料をどのように調節するかについて述べる。
① 嫌気用試料管の作製
スプラジル石英管とパイレックス管が段継されている EPR 試料管を準備し、図7に示した方法でパイレックス試験管を EPR 試料管上部にガラス細工溶接をする。EPR に関する高精度石英ガラス加工業者としては、株式会社アグリ(http://www.kk-agri.co.jp 青梅市)がある。しかし、この程度のガラス細工溶接は自分自身でできる。
② 真空ラインによる脱気
図8のような真空ラインを用いて EPR 試料管内の試料を嫌気状態にする。
- EPR 試料管の最下部に試料を入れてから脱気すると、真空引きをやり過ぎて試料からアワが出たりするので注意しなければならない。試料管上部の太めのパイレックス部分に試料を入れて脱気/窒素ガス導入をする方がガス交換の効率が良く、安全である。
- 試料を入れずに先ず EPR 試料管内を脱気する。+0.2 気圧程度加圧した窒素ガスで満たし、別途嫌気状態で調整した試料を気密マイクロシリンジで注入する方法が安全である。(試料管内を1気圧より高くするのは試料注入時に空気が入るのを防ぐためである。)別途嫌気状態で調整した試料(窒素ガスで加圧されていることが重要)は脱気洗浄した気密マイクロシリンジ内に取り込み、嫌気状態の EPR 試料管に注入する。
③ マイクロシリンジ内の脱気・洗浄法、嫌気試料の取り扱い
脱気したマイクロシリンジは、図9の手順で用意する。
- ネジキャップセプタム付きパイレックス試験管に脱イオン水を 1/4~1/5 程入れて、真空ラインを用いて、充分に脱気と窒素ガス注入を繰り返す。最後に、窒素ガスで +0.2 気圧程度加圧した状態にする。この試験管のセプタム部分を図9右図のように下に向けて、下方より上向きに気密マイクロシリンジの注射針を差し込むとシリンジ内に嫌気脱イオン水が窒素の圧力で押し込まれてくる。この脱イオン水を押し出してシリンジ内を一度洗浄する。
- 微小量の試薬、試料を嫌気状態で取り扱う場合には、底部が細くなった小さなミニバイアルを用いると便利である。上方からマイクロシリンジの針をセプタム部に突き刺し、注射針をバイアル底部まで刺し込んで試薬や試料溶液を吸い上げる。
- EPR 試料管の上部から試料溶液を注入することになるので、試料管の最下部の測定部分まで試料を落とさなければならない。そのため、試料導入後一気に振り下ろして、氷中にしばらく静置する。かなりの試料が試料管壁に付くので、使用する試料の量は少し多めにする必要がある。
- 酸素分子を嫌う還元剤や配位性気体分子(一酸化窒素(\(\ce{NO}\))や一酸化炭素(\(\ce{CO}\)))などの反応試薬も、同様の手法で EPR 試料管に注入できる。
- グローブボックス内で嫌気的に試料を調整し、試料管への充填や封じこみ、更には凍結まで行うこともある。
3-3 単結晶試料の EPR 測定
常磁性物質の \(g\) 因子(\(g\) 値)、微細構造定数、超微細構造定数(核結合定数)はすべてテンソル量である。溶液試料の EPR からは、これらテンソルの主値の平均値が決まるだけで、主軸の方向についての情報は得られない。単結晶試料の EPR 解析からこれらテンソルを明確に決定することが可能になる。また、結晶内での不対電子の分布情報が得られる。特に、X 線結晶構造解析で分子構造が決められている金属タンパク質の単結晶 EPR を観測することで、活性中心の金属イオンと周りのアミノ酸残基との間の相互作用、不対電子の分布する軌道、補欠分子の向き、などについての詳細な解析が可能になる。ここでは、タンパク質の単結晶で EPR 測定をする際の一般的なテクニックと問題点について述べる。単結晶 EPR データの解析法については、後節でまとめて紹介する。
3-3-1 タンパク質の単結晶
タンパク質の結晶を作成することから結晶解析が始まるが、結晶作製については他書を参考にされたい。ここでは、X 線結晶構造解析に使われるタンパク質の単結晶を前提とする。タンパク質の結晶の EPR 測定は、無機結晶や低分子有機化合物の結晶の場合と同様に考えればよい。しかし、タンパク質の結晶は無機結晶などよりはるかに壊れやすいので、取扱いは十分丁寧に行わなければならない。また、結晶中の水分が失われると、結晶は壊れてしまうので、結晶を取り扱うときは常に結晶母液と共存させる必要がある。
- 結晶中で分子は3次元的に規則配列をしている。この規則性の最小単位を単位胞という。
- 単結晶 EPR で使える良い結晶とは、X 線結晶構造解析と異なり、最低でも長辺 0.5 mm 以上の大きさは欲しい。単位胞中の分子数が少なく、強い信号を出す場合ではもっと小さくても可能である。肉眼で単結晶が取り扱えることが重要である。顕微鏡下でなければゴニオメーターの結晶マウント(後述)にセットできないような小さな単結晶では、EPR 信号の測定・解析は無理と思った方が良い。
- EPR 観測の前に、「単位胞の中に何個の分子が、どのような空間群、対称性をもって存在するのか」の情報が必要である。X 線結晶構造解析から、単結晶の結晶軸の向きが判明していることが必要である。
- 顕微鏡下あるいは肉眼で結晶をよく観察し、スケッチを行うと共に面角を測る。これらの作業から、結晶主軸の向きを頭の中に叩き込むことは重要である。
メモ
3-3-2 単結晶試料をEPRゴニオメーターに取り付ける
単結晶試料を簡単な結晶マウントに取り付け、軸まわりで回転させてデーターを得る。図10-Aに一軸回転用ゴニオメーターの結晶マウントに単結晶をセットする方法を示す。
(I)と(II)は、一つの結晶面内での角度変化を測定する場合に用いる。(III)は、結晶の任意の方向に磁場を当てたいときに使う。(III)の結晶回転台はテフロンで作られており、縦の回転を行うには、一角度測定する毎に結晶支持ロッドを引き上げて手動で回転させる。この作業は熟練が要求されるが、慣れるとかなりの精度で再現性が得られる。
小さな歯車を使って、二軸まわりの回転角度を上部にある二つの角度目盛りで読み取る二軸回転用の EPR ゴニオメーターも考案されている。しかし、大きさ、強度、精度面で液体窒素温度の測定が限界であろう。
①単結晶の取り付け
タンパク質の単結晶を結晶マウントに取り付ける。この際に、「接着剤」は結晶母液が最適である。単結晶を結晶マウントに取り付ける方法を図11に示す。
- ポリエチレンチューブで作製した長さ 10 cm 程度の自在ピペットを使って1個の単結晶を母液ごと吸い上げる。小さなシャーレに数個の結晶を母液ごと移しておくとよい。
- 結晶を吸い上げたピペットを下に向けると重力によって結晶がピペットの先端に来る。
- 結晶マウント上に(ピペットの先端が結晶に触れないように)静かに結晶と母液を押し出す。このとき、母液の表面張力のため、結晶はマウント上の母液の水玉の中に浮いた状態になる。10 cm 程度の円形ロ紙を16等分した扇形のロ紙片を作って、鋭角ロ紙片が結晶に触れないように注意深く母液を吸い取る。単結晶の結晶軸の向きを結晶回転軸に対して正しくセッティングする作業は肉眼で行うが、誤差の原因になるので正確、慎重に行う。
- 室温測定の場合の注意点は以下の通りである。まず、単結晶がマウントからズレたりしないように、高真空用真空グリースで結晶を覆う。爪楊枝などでグリースを糸状に伸ばして結晶を覆うとよい。結晶中の水分が失われないようにするためには、図10-Bの様に結晶回転ロッドを EPR 試料管内に封入する。さらに、試料管の底部が空洞共振器の外に出る程度に長くして、試料管の底部に結晶母液を少し入れておく。測定中は結晶の温度が変化しないように、温度制御した空気か窒素ガスを共振器内に流すことを忘れない!
- 低温測定の場合、結晶の凍結作業に注意を払う。液体窒素を満たした小さな発泡スチロール容器に、結晶支持ロッドを先端から挿入して、ゆっくりと結晶を凍らせる。このとき、マウントと結晶の間の母液が凍って接着剤の役割をする。急激に凍らせると結晶が弾け飛んでしまうことがあるので注意する。これを防ぐために、結晶マウントに細かい網目を刻んでおくと効果的である。
- 液体ヘリウムのフロークライオスタットで測定する場合、図10-Aの結晶回転軸を直接フローデュワーに挿入すると、フローガスの勢いで結晶がマウントから落下してしまう危険性がある。そこで、図10-Bに示すように、結晶回転軸を EPR 試料管の中に封入する方法をとる。そのため、結晶回転軸として、外径 2.8 mm φ 程度のアクリルかデルリンのロッドを細工する。結晶マウント部は図10-Aの(I)や(II)と同様な細工をする。結晶マウントが小さいため、使用できる結晶も小さくなる。
②嫌気状態での単結晶の取扱い
ヘムタンパク質の EPR 測定では、一酸化窒素(\(\ce{NO}\))のように、酸素を嫌う気体分子をヘム鉄に配位させることがよくある。\(\ce{NO}\) 配位型の単結晶試料を用意するには、一旦還元型の結晶を用意した後に、\(\ce{NO}\) を配位させる。
- はじめに、還元型のヘムタンパク質の単結晶を作る。酸化型の単結晶を浮遊させた結晶母液に、窒素ガスを静かにバブリングして脱気を行う。次に、ハイドロサルファイト等の還元剤でヘム鉄を還元し、還元型の結晶を得る。
- しかし、還元によって分子構造が変化するタンパク質の場合は、還元することで結晶が壊れる危険性がある。この場合は、最初から還元型で結晶化させた単結晶を準備する必要がある。
以上の手法で還元型ヘムタンパク質の単結晶を得た後に、\(\ce{NO}\) ガスを配位させる。このステップの詳しい方法を図12に示す。
メモ
3-3-3 単結晶を回転させるときの問題点
① 結晶軸の回りに正しく回転させているかをチェックする。
単斜晶系、空間群が \(P_{2_{1}}\)、単位胞中に2分子がある単結晶を例に考えてみよう(図13)。この単結晶では、\(\boldsymbol{a}\)-軸、\(\boldsymbol{b}\)-軸、\(\boldsymbol{c}\)-軸の長さは全て異なっている(\(\boldsymbol{a} \ne \boldsymbol{b} \ne \boldsymbol{c}\))。\(\boldsymbol{b}\)-軸と \(\boldsymbol{c}\)-軸のなす角度(\(\alpha\))と \(\boldsymbol{a}\)-軸と \(\boldsymbol{b}\)-軸のなす角度(\(\gamma\))は等しく90°である。\(\boldsymbol{a}\)-軸と \(\boldsymbol{c}\)-軸のなす角度を \(\beta\) とする。そこで、\(\boldsymbol{ab}\) 面に垂直な向きに仮想的な \(\boldsymbol{c^{\ast}}\)-軸を考える。ここでは \(\boldsymbol{b}\)-軸が \(P_{2_{1}}\) の2回らせん対称軸である。単結晶 EPR の解析では2回らせん対称も2回対称も分子に対する外部磁場の向きは同じに扱えるが、結晶の裏と表の関係に注意しなければならない。
先ず、\(\boldsymbol{ab}\) 面内で結晶を回転させてみよう(\(\boldsymbol{c^{\ast}}\)-軸の回りの回転である)。結晶を例えば10°刻みで回転させて、その都度 EPR スペクトルを記録していくとしよう。
- この結晶は単位胞中に2分子あるので、2本の EPR 信号が角度変化することが分かる。
- 結晶の対称性より、外部磁場と結晶軸が平行になると EPR 信号は1本に重なる。90°毎に EPR 信号は1本になり、結晶軸(\(\boldsymbol{a}\)-軸、\(\boldsymbol{b}\)-軸)が判別できる。結晶が正しく \(\boldsymbol{c^{\ast}}\)-軸の回りで角度変化していないと、180°回転時に得られる EPR スペクトルは最初(0°)の EPR スペクトルとずれてしまう。
- 単結晶 EPR の解析では横軸に回転角度を、縦軸に \(\boldsymbol{g}\)-値の二乗をプロットする(図14)。プロットで明らかなように、結晶が正しくゴニオメーターにマウントされていると結晶軸の前後で対称な2本の曲線が得られるはずである。この点を確認するために、\(\boldsymbol{g^{2}}\)-プロットを作る前に回転角度順に EPR スペクトルを並べて(横軸は磁場)、結晶軸の前後でスペクトルが対称に変化しているかどうかをチェックする。2本の曲線が対称でない場合、結晶は正しく回転していないので、やり直す。
次に、この結晶の2回らせん対称軸(\(\boldsymbol{b}\)-軸)回りでの角度変化を調べる。対称性から、EPR 信号は1本になるはずである。2本の信号が観測される場合は、結晶軸の採り方が間違えているか、回転軸が \(\boldsymbol{b}\)-軸から少しずれていることを示しているので、やり直す。
- \(\boldsymbol{ac}\) 面内(\(\boldsymbol{b}\)-軸での回転)の場合、得られる角度変化の曲線は1本になるので、曲線のどこが \(\boldsymbol{a}\)-軸、\(\boldsymbol{c}\)-軸あるいは \(\boldsymbol{c^{\ast}}\)-軸であるかを決めることは難しい。特に、\(\boldsymbol{c}\)-軸方向の \(\boldsymbol{g}\)-値に関しては結晶の裏表の区別が必要である。先にも述べたように、結晶をマウントする前に、顕微鏡下あるいは肉眼で結晶をよく観察して結晶主軸の向きを頭の中に叩き込むことが重要になる。\(\boldsymbol{c^{\ast}}\)-軸方向の \(\boldsymbol{g}\)-値(\(\boldsymbol{g_{c^{\ast}}}\))に関しては、\(\boldsymbol{a}\)-軸での回転(即ち \(\boldsymbol{bc^{\ast}}\) 面内での角度変化)より求める。\(\boldsymbol{a}\)-軸方向の \(\boldsymbol{g}\)-値(\(\boldsymbol{g_{a}}\))は \(\boldsymbol{ab}\) 面内の結果より対応できる。
② 二軸回転ゴニオメーターを使う利点
一軸回転ゴニオメーターの場合、解析のためには少なくとも3個の単結晶を用意しなければならない。それに対して、二軸回転ゴニオメーターでは1個の単結晶があれば少なくとも一組のデータを得ることができる。従って、貴重な単結晶標品を有効に使うことができる。また、二軸回転ゴニオメーターを使うことで、単結晶のどのような向きにでも外部磁場を当てることが可能になるため、例えば、ヘムタンパク質のヘム面に垂直な向きに磁場を与えるなどの応用が容易である。しかし、二軸回転ゴニオメーターとして普及しているのは、液体窒素温度と室温用のみである。液体ヘリウムのフロークライオスタット用に関しては、工作上(強度)、精度上の問題があり一般用に作られていないが、図10で紹介した方法で測定できる。
3-3-4 単結晶 EPR の解析法
常磁性物質の \(\boldsymbol{g}\) 因子(\(\boldsymbol{g}\) 値)、微細構造定数、超微細構造定数(核結合定数)はすべてテンソル量であることは既に述べた。溶液試料の EPR からは、これらテンソルの主値の平均値が決まるだけで、主軸の方向についての情報は得られない。単結晶試料の EPR 解析からこれらテンソルを決定することができる。
ここでは、\(\boldsymbol{g}\) 因子(\(\boldsymbol{g}\) 値)の異方性と \(\boldsymbol{g}\) 主値の求め方について解説する。\(\boldsymbol{g}\) 因子の異方性は、実験室系の任意の直交座標 \((\boldsymbol{a}\text{、}\boldsymbol{b}\text{、}\boldsymbol{c})\) と分子の対称性にもとづく \((\boldsymbol{x}\text{、}\boldsymbol{y}\text{、}\boldsymbol{z})\) の2つの座標系で記述できる。実験室系における \(\boldsymbol{g}\) テンソル(\(\boldsymbol{\tilde{g}}\))の9個の成分は3行3列の正方マトリックスで表される。一方、主軸系 \((\boldsymbol{x}\text{、}\boldsymbol{y}\text{、}\boldsymbol{z})\) では主値 \(\boldsymbol{g_{xx}}\)、\(\boldsymbol{g_{yy}}\)、\(\boldsymbol{g_{zz}}\) のみの対角行列となる。したがって、実験室系で得られた3行3列の行列を対角化する主軸変換を行うことで、主軸系の主値を求めることができる。
\[\begin{array}{llll} \tilde{g} = & \left( \begin{array}{ccc} g_{aa} & g_{ab} & g_{ac} \\ g_{ba} & g_{bb} & g_{bc} \\ g_{ca} & g_{cb} & g_{cc} \end{array} \right) & \xrightarrow{\mbox{主軸変換}} & \left( \begin{array}{ccc} g_{xx} & 0 & 0 \\ 0 & g_{yy} & 0 \\ 0 & 0 & g_{zz} \end{array} \right) \\ & \text{実験室系} (\boldsymbol{a}\text{、}\boldsymbol{b}\text{、}\boldsymbol{c}) & & \text{主軸系} (\boldsymbol{x}\text{、}\boldsymbol{y}\text{、}\boldsymbol{z}) \end{array}\]結晶に固定した結晶座標系(ここでは、\(\boldsymbol{a}\)、\(\boldsymbol{b}\)、\(\boldsymbol{c}\) 結晶軸が直交する場合を考える)を用いて実験すると、外部性磁場の方向余弦 \((l\text{、}m\text{、}n)\) に対する \(\boldsymbol{g}\) 因子の測定値 \(\boldsymbol{g}(l\text{、}m\text{、}n)\) の2乗は
\[g^{2} (l\text{、}m\text{、}n) = G_{aa} l^{2} + G_{bb} m^{2} + G_{cc} n^{2} + 2(G_{ab}lm + G_{bc}mn + G_{ca}nl) \tag*{[2]}\]となる。\(\boldsymbol{G_{ij}}\) は対称テンソル \(\tilde{g} \cdot g = G\) の \((\boldsymbol{a}\text{、}\boldsymbol{b}\text{、}\boldsymbol{c})\) 座標系の行列要素である。\(\boldsymbol{G_{aa}}\)、\(\boldsymbol{G_{bb}}\)、\(\boldsymbol{G_{cc}}\) は結晶の \(\boldsymbol{a}\)-、\(\boldsymbol{b}\)-、\(\boldsymbol{c}\)-軸方向の \(\boldsymbol{g}\)-値より直ちに決定できる。非対角要素 \(\boldsymbol{G_{ij}}\) は図15に示したように、\((\boldsymbol{ij})\) 面内での \(\boldsymbol{g}^{2}\) –回転角度プロットより決定する。図15は \(\boldsymbol{ab}\) 面内の回転(\(\boldsymbol{c}\)-軸回し)を示したもので、180°を周期とする正弦関数となる。
\(\boldsymbol{G_{ab}}\) は
\[G_{ab} = \dfrac{1}{2}(G_{max} - G_{min}) \cdot \sin(2\phi_{max}) \tag*{[3]}\]より求められる。ここで、\(\boldsymbol{G}_{max}\)、\(\boldsymbol{G}_{min}\) は \(\boldsymbol{g}^{2}\) プロットの最大値と最小値である。\(\phi_{max}\) は図15で説明するならば、\(\boldsymbol{a}\)-軸から \(\boldsymbol{G}_{max}\) までの回転角度になる。\(\boldsymbol{G_{ab}}\) の符号が問題になるが、\(\phi = 0 \rightarrow 90°\) にともなって \(\boldsymbol{g}\) 因子が増大するときを正にとり、減少するときを負にとる。同様に \(\boldsymbol{bc}\)、\(\boldsymbol{ac}\) 面内での \(\boldsymbol{g}^{2}\)–回転角度プロットより全ての非対角要素 \(\boldsymbol{G_{ij}}\) が求まる。
\[\begin{array}{llllll} \tilde{G} = & \left( \begin{array}{ccc} G_{aa} & G_{ab} & G_{ac} \\ G_{ba} & G_{bb} & G_{bc} \\ G_{ca} & G_{cb} & G_{cc} \end{array} \right) & \xrightarrow{\mbox{対角化}} & \left( \begin{array}{ccc} G_{xx} & 0 & 0 \\ 0 & G_{yy} & 0 \\ 0 & 0 & G_{zz} \end{array} \right) & \rightarrow{\mbox{ }} & \left( \begin{array}{ccc} {G^{2}}_{xx} & 0 & 0 \\ 0 & {G^{2}}_{yy} & 0 \\ 0 & 0 & {G^{2}}_{zz} \end{array} \right) \end{array}\]\(\boldsymbol{G}\) テンソルを対角化することによって、\(\boldsymbol{G}\) テンソルの主値及び主軸変換行列から主軸方向が求まる。\(\boldsymbol{g}\) が対称テンソルの場合には、\(\boldsymbol{g}\) の主軸は \(\boldsymbol{G}\) の主軸と一致し、\(\boldsymbol{g}\) 主値は \(\boldsymbol{G}\) の主値の平方根で与えられる。
次に、溶液の EPR スペクトルが軸対称性を示す場合(\(g_{xx} = g_{yy} = g_{\perp}\)、\(g_{zz} = g_{\parallel}\))を考える。この場合、単結晶 EPR の取り扱いは簡単になる。外部磁場 \(\boldsymbol{B}\) を分子の \(\boldsymbol{z}-\)主軸(\(g_{\parallel}\) 方向)と角度 \(\theta \text{°}\) をなす方向にかけたときのみかけの \(g\) 値(\(g_{\theta}\))は、\(g_{\perp} > g_{\parallel}\) として、
\[{g_{\theta}}^{2} = {g_{\parallel}}^{2} \cos^{2}\theta + {g_{\perp}}^{2} \sin^{2}\theta = {g_{\parallel}}^{2} + ({g_{\perp}}^{2} - {g_{\parallel}}^{2}) \cdot \sin^{2}\theta \tag*{[4]}\]で表わされる。
結晶 \(\boldsymbol{ab}\)、\(\boldsymbol{bc}\) 、\(\boldsymbol{ac}\) 面の少なくとも2面で \(g^{2}\) の角度変化を測定して、\(g_{a}\)、\(g_{b}\)、\(g_{c}\) を求める。\(g_{a}\) より直ちに \(\boldsymbol{a}\)-軸と \(\boldsymbol{z}\)-主軸のなす角度が、同様に \(\boldsymbol{g_{b}}\)、\(\boldsymbol{g_{c}}\) の値より \(\boldsymbol{b}\)-、\(\boldsymbol{c}\)-軸と \(\boldsymbol{z}\)-主軸のなす角度が決まる。従って、結晶 \(\boldsymbol{a}\)-、\(\boldsymbol{b}\)-、\(\boldsymbol{c}\)-軸に対する \(\boldsymbol{z}\)-主軸(\(g_{\parallel}\))の方向余弦が求まる。当然、これらの方向余弦の2乗の和が1になっていなければならない。
ステレオ投影法を用いると、\(g_{\parallel}\) 方向や \(g_{\perp}\) 面が結晶中でどの様になっているか理解し易い。ステレオ投影法については図16に示す。図16-Cのステレオグラフ用紙(ウルフネット)を透明な用紙に拡大コピーして、結晶EPR解析用に利用するとよい。
\(\boldsymbol{g}\) 因子同様、微細構造定数、超微細構造定数はすべてテンソル量である。\(\boldsymbol{g}\) 因子テンソルの解析と同様に主値、主軸の方向を決定することができる。
4. ヘムタンパク質の EPR
ヘムタンパク質を研究対象にしていると、どうしても EPR の測定が必要になるときがある。ここまで述べてきたことを基本にして、具体的なヘムタンパク質の EPR 測定について解説する。
4-1 酸化型ヘムタンパク質
ヘムタンパク質のヘム鉄は、還元型(\(\ce{Fe^{2+}}\))にも酸化型(\(\ce{Fe^{3+}}\))にも、さらには中間体としての高酸化状態(\(\ce{Fe^{4+}}\) または \(\ce{Fe^{5+}}\))にもなる。表1で示したように、普通の装置で EPR スペクトル測定が可能なのは、酸化型ヘム鉄のように半整数スピン系のヘムタンパク質が主になる。酸化型の鉄は、外部磁場がないときはクラマース2重項とよばれるスピン縮退の状態にあるが、外部磁場が加わるとこの縮退が解けてゼーマン分裂がおこり、EPR 遷移が観測される。理論的なことは他書にゆずり、ここでは、基礎的な事項についての簡単な説明と、実験的に何が観測されどう解釈するかについて述べる。
メモ
4-1-1 高スピン状態の酸化型ヘム鉄(\(\boldsymbol{S = 5/2}\))の EPR
自由な \(\ce{Fe^{3+}}\) イオンの基底状態は、5個の電子が5個の \(3d\) 軌道に一つずつ入ってスピン6重項状態であり 6S と表わされる。同様に、ポルフィリン環内の \(\ce{Fe^{3+}}\) イオンの基底状態は、配位子場が C4v の対称性を持つため、6A1 と表わされるスピン6重項状態である。この状態のスピン量子数は \(S = 5/2\) であり、高スピン状態(high spin)と呼ばれる。
ポルフィリン環による配位子場の対称性が下がると、スピン–軌道相互作用によって励起状態(4T1)の波動関数が基底状態の 6A1 に少し混ざってくる。その結果、基底状態は3個のスピン2重項(クラマース2重項 \(S_{z} = \pm 1/2\)、\(\pm 3/2\)、\(\pm 5/2\))に分裂する。この基底状態のエネルギー分裂はスピンハミルトニアン
\[\mathrm{H} = D \left( S_{z}^{2} - \dfrac{S(S + 1)}{3} \right) + E \left( S_{x}^{2} - S_{y}^{2} \right) + 2 \beta S \cdot B \tag*{[5]}\]で表わされる。ここで、\(\boldsymbol{D}\) はヘム面に垂直方向(軸方向)の異方性の大きさ、\(\boldsymbol{E}\) はヘム面内の異方性の大きさ(対称性の低さ)を示すパラメーターである。\(D\) が大きいとき(\(D \gg 2 \beta B\))に外部磁場 \(B\) を加えると、これらの3つのクラマース2重項の縮退が解けて、いちばん最低準位の2重項(\(S_{z} = \pm 1/2\))のゼーマン分裂による EPR が観測される。これが、高スピン状態の酸化型ヘム鉄に通常観察される EPR 信号である。一方で、通常の EPR 装置のマイクロ波周波数では \(S_{z} = \pm 1/2 \leftrightarrow S_{z} = \pm 3/2\) の遷移は観測できない。
① 配位子場が正方対称場の場合 → 軸対称な EPR スペクトルについて
ヘム面に垂直な方向を \(z\) 軸にとり、ヘム面が軸対称な場合を考える。上記のスピンハミルトニアンを \(E = 0\) として、\(S = 5/2\)、\(S_{z} = \pm 1/2\) で解くと、見掛けの \(g\) 値(\(hν = g \beta B\) より求まる)は \(g_{\mathrm{x}} = g_{\mathrm{y}} = g_{\perp} = 6.0\)、\(g_{z} = g_{\parallel} = 2.0\) で与えられることが分かる。これは、ヘム面に垂直な方向(z 軸)に外部磁場が加わると \(g_{\parallel} = 2.0\) を示し、ヘム面に平行に磁場が加わると \(g_{\perp} = 6.0\) を示すということである。このタイプの EPR スペクトルを図17-Aに示す。第6配位座に水分子が配位したミオグロビン(Mb)、ヘモグロビン(Hb)が典型的な例である(アコメト Mb とかアコメト Hb と云う)。このような形状を、軸対称な EPR スペクトルと呼ぶ。
-
アコメト Mb について単結晶解析を行うと、\(g\) 値はわずかに異方性を示しているが、溶液のスペクトルでは線幅に隠れて異方性の分裂は見られない。単結晶試料を外部磁場に対して角度変化させ、\(g_{\parallel} = 2.0\) の信号を探し出すと、結晶中のヘム面方位が決定できる。ヘム法線方向に磁場が平行にかかると、\(g = 2\) 信号の線幅がせまくなり、同時に信号強度が急激に増大する。軸対称な系での単結晶 EPR 解析法は前章で述べたが、\(g_{\perp} = 6.0\)、\(g_{\parallel} = 2.0\) とすれば \([4]\) 式より、
\[g_{\theta} = 2\sqrt{1 + 8\sin^{2}\theta} \tag*{[6]}\]が得られる。従って、単結晶の結晶軸方向に磁場をかければ、結晶軸とヘム法線とのなす角度が計算できる。
- 軸対称な高スピン酸化型ヘム鉄の \(g_{\perp} = 6.0\) 信号は一次微分曲線の最大ピーク値のところをとる。図18に軸対称な無秩序配向 EPR スペクトルの \(g\) 因子を示す。軸対称な無秩序配向 EPR スペクトルの \(g\) 因子についての理論的な解説は文献を参考にされたい(11, 12)。
- マイクロ波周波数が既知の場合に、高スピン型アコメト Mb を磁場の校正に使用できる。すなわち、アコメト Mb の溶液 EPR スペクトルを測定することで \(g_{\perp} = 6.0\)、\(g_{\parallel} = 2.0\) の磁場が求められるので、これらの信号を参照することで、他の試料の \(g_{\perp} = 6.0\text{~}2.0\) の間に現れる信号の \(g\) 値が計算できる。参照試料としては、アコメト Mb より \(\ce{NaF}\) を加えた MbF(フルオロメト Mb)の方が、線幅が狭く、信号強度も強いので精度がよい。フルオロメト Mbの場合、フッ素の核スピン(\(I = 1/2\))によって \(g_{\parallel} = 2.0\) が2本に分裂する。また、\(g_{\perp}\) 信号に hfs は見られない。
- アコメト Mb や Hb は室温では線幅増大のため EPR スペクトルの観測は不可能である。MbF では、信号強度は低いが室温での観測が可能である。
- 高スピン型ヘムタンパク質の場合、測定温度を低くすればする程 EPR の信号強度は増大する。マイクロ波による飽和現象も起こり難いので、マイクロ波出力をある程度強くしても正しいスペクトルが観測される。したがって、高スピン型ヘムタンパク質の EPR 観測では試料濃度をかなり低くできる。高スピン種のみの場合なら、試料濃度が 10 μM、試料体積 50 μL 程度で測定できる。
② ヘム面内に異方性がある場合
ヘムの配位子場が正方対称場から斜方対称場に対称性が低下すると、図17-Bに示すように \(g_{\perp} = 6.0\) 信号に分裂がみられる。この分裂は前記スピンハミルトニアンで \(E \ne 0\) とすることで、二次摂動計算より次のように求められる。
\[\begin{align} g_{x} &= 6 + 24 \dfrac{E}{D} + O \left( \dfrac{1}{D^{2}} \right)\\ g_{y} &= 6 - 24 \dfrac{E}{D} + O \left( \dfrac{1}{D^{2}} \right) \hspace{10mm} \Delta_{g} = (g_{x} - g_{y}) = 48 \dfrac{E}{D}\\ g_{z} &= 2 - O \left( \dfrac{1}{D^{2}} \right) = g_{\parallel} \end{align} \tag*{[7]}\]ここで、\(O \left( \dfrac{1}{D^{2}} \right)\) は \(\dfrac{1}{D^{2}}\) より高次の項を表す。式 \([7]\) は、\(g_{\perp}\) 信号が \(g = 6\) を中心に分裂すると同時に、\(g_{\parallel}\) 信号が \(g = 2\) から高磁場側にシフトすることを示している。実際には、多くのヘムタンパク質のEPRの測定結果では、\(g_{\perp} \sim 6.0\)、\(g_{\parallel} \sim 2.0\) である。したがって、\(E/D\) は \(\sim 1/100\) 程度の値である。
- EPR で決められるのは \(E/D\) であり、\(D\) や \(E\) の値を直接決めるには、多周波数(特に高周波数マイクロ波)・強磁場 EPR で直接励起準位との遷移を測定するか、磁化率測定が必要である。\(D\) の値は 10 cm-1 前後であるから、エネルギー遷移幅が 0.3 cm-1 程度の通常の EPR では、全く観測が不可能であることが分かる。
③ \(\boldsymbol{E/D}\) は \(\boldsymbol{\Delta g = g_{x} - g_{y}}\) で与えられる
\(g_{\perp}\) 信号の分裂は、ヘムの正方対称性が崩れていることを示す指標となる。また、ヘムタンパク質が固有の機能、活性を発現するとき、ヘム周辺の構造変化を伴う場合が多いが、この構造変化に伴って \(g_{\perp}\) 信号の分裂に影響がみられることがよくある。
- ヘムの正方対称性が崩れている例として、第5(近位)配位座の軸配位子のチロシンやシステインが、フェノレート(\(\ce{O^{-}}\))やチオレート(\(\ce{S^{-}}\))として5配位構造をとる場合が挙げられる。カタラ―ゼ(\(g_{\mathrm{x}} = 6.6\)、\(g_{\mathrm{y}} = 5.4\)、\(g_{\mathrm{z}} = 2.03\))や P450cam(\(g_{\mathrm{x}} = 7.87\)、\(g_{\mathrm{y}} = 4.00\)、\(g_{\mathrm{z}} = 1.77\))、ミエロペルオキシダーゼ(\(g_{\mathrm{x}} = 6.74\)、\(g_{\mathrm{y}} = 5.18\)、\(g_{\mathrm{z}} = 1.97\))などの具体例である。
- ヒスチジンが配位しているヘムタンパク質の場合でも、ヒスチジンのイミダゾール基がイミダゾレート(\(\ce{Im^{-}}\))的な性質を持つ場合に、\(g_{\perp}\) 信号の分裂が観測される。ペルオキシダーゼなどが具体例である。
- ヘムタンパク質の構造変化に伴い、第6(遠位)配位座側の配位環境(極性など)が変化すると、ヘム面内の異方性信号(\(g_{\perp} = 6.0\) 信号の分裂)が観測できる。このような変化を捉えるために、僅かな \(g_{\perp}\) 値の変化も見落としてはならない。高スピン信号の場合はできるだけ測定温度を低くして線幅を減少させ、\(g_{\perp}\) 値の分解能を上げることである。77 K では変化が捉えられないが、5 K での測定で変化が捉えられた例はよくある。\(g_{\perp} = 6.0\) 信号の分裂に変化が見られたかどうかを調べるときには、例えば \(g_{\mathrm{x}}\) 信号が低磁場側にシフトしたとき、一方の \(g_{\mathrm{y}}\) 信号が高磁場側にシフトすれば \(g_{\perp} = 6.0\) 信号の分裂のしかたに変化があったことを示している。
- 使用する緩衝液の種類、pH によっても \(\Delta g\) が変化する場合がある。
- グリセロールやエチレングリコール等を混ぜた系では、ヘム周辺の水分子の影響が変化するため、ヘム面内の異方性信号に変化がみられることがある。
④ \(\boldsymbol{g = 4.3}\) の信号について
酸化型ヘムタンパク質の EPR 測定で、しばしば \(g = 4.3\) の信号が問題になる。理論的には、例えば、\(E/D = 1/3\) とすることで、等方的な \(g = 4.3\) 信号と \(g = 9.3\) 近傍の信号を説明できる。しかし、この帰属の前に、\(g = 4.3\) の信号が観測されたら、試料の変性の可能性を疑うべきである。酸化型ヘムタンパク質の精製過程で変性などがおこると \(g = 4.3\) に EPR 信号がみられることはよく知られている。従って、ヘム近傍に何か構造的な「変性」が生じたかもしれないと考え、タンパク質のチェックをするべきである。この場合の \(g = 4.3\) 信号は、ヘムから外れた \(\ce{Fe^{3+}}\) に由来する可能性がある。例えば、非ヘムタンパク質で、鉄–硫黄タンパクのルブレドキシン酸化型は \(\ce{Fe^{3+}}\) 高スピン(\(S = 5/2\))由来の特徴的な \(g = 4.3\) 信号を示すことが知られている。
4-1-2 低スピン状態の酸化型ヘム鉄(\(\boldsymbol{S = 1/2}\))の EPR
ヘム鉄の上下に強い配位子場を与える配位子が結合すると、2重縮退の \(e_{\mathrm{g}}\) 軌道と3重縮退の \(t_{\mathrm{2g}}\) 軌道(\(d_{xy}\)、\(d_{yz}\)、\(d_{zx}\))の分裂が広がるため、5個の \(3d\) 電子はすべて \(t_{\mathrm{2g}}\) 軌道に入った電子状態は \((t_{\mathrm{2g}})^{5}\) となる。このとき、全スピン数は \(S = 1/2\) の低スピン(low spin)状態になる。\(t_{\mathrm{2g}}\) 軌道は6個の電子で完全に閉殻となるから、近似的に1個の空孔(hole)が \(t_{\mathrm{2g}}\) 軌道に在ると考えることもできる。従って、多電子系での計算が \((3d)^{1}\) の hole の計算で近似できる。
低スピン状態における配位子場が、z 軸方向に軸対称性歪(\(\boldsymbol{\mu}\))やヘム xy 面内の歪(\(\boldsymbol{R}\))を受けると、\(t_{\mathrm{2g}}\) 軌道の縮退が解けて3つのクラマース2重項に分裂する。さらに、スピン–軌道相互作用によりこの3つの2重項状態が混ざり合って、軌道1重でスピン2重項の新しい3つの軌道 \(\xi(d_{\mathrm{yz}})\)、\(\eta(d_{\mathrm{xz}})\)、\(\zeta(d_{\mathrm{xy}})\) になる。Gibson はアジド(\(\ce{N3^{-}}\))が結合した6配位型の酸化型ヘモグロビンの \(\boldsymbol{g}\) テンソル(\(g\) 主値は \(g_{\mathrm{xx}} = 1.72\)、\(g_{\mathrm{yy}} = 2.22\)、\(g_{\mathrm{zz}} = 2.80\))の解析を行い、ヘム面に対する主軸の向きを決定した(13)。図17-Cに典型的な低スピン型ヘムタンパク質の EPR スペクトルを示す。Griffith は低スピン EPR の \(g\) 因子を用いて \(t_{\mathrm{2g}}\) 軌道のエネルギー準位を解析する理論を提唱した(14)。\(t_{\mathrm{2g}}\) 軌道のエネルギー状態を図19に示す。このように、低スピン状態の酸化型ヘム鉄の EPR スペクトルを解析することで、最低準位のクラマース2重項の波動関数を実測の異方性 \(g\) 因子(\(g_{\mathrm{x}}\)、\(g_{\mathrm{y}}\)、\(g_{\mathrm{z}}\))より計算し、ヘムの対称性(\(\boldsymbol{\mu}\)、\(\boldsymbol{R}\))が議論できる。同様の解析法が Taylor(15) によっても報告されている。
① \(\boldsymbol{g}\) 因子からどのような計算をするのか?
最低準位のクラマース2重項のスピン軌道関数を
\[\begin{align} \Psi ^{+} &= A \xi^{+} + iB \eta^{+} + C \zeta^{-} \\ \Psi ^{-} &= -A \xi^{-} + iB \eta^{-} + C \zeta^{+} \end{align} \tag*{[8]}\]とおく。これより \(g\) テンソル主値は、
\[\begin{align} g_{xx} &= 2|(B + C)^{2} - A^{2}| \\ g_{yy} &= 2|(A - C)^{2} - B^{2}| \\ g_{zz} &= 2|(A - B)^{2} - C^{2}| \end{align} \tag*{[9]}\]で表わされる。観測された \(g\) 主値を用いて係数 A、B、C が決定される。
ここで、\(\xi (d_{\mathrm{yz}})\)、\(\eta (d_{\mathrm{xz}})\)、\(\zeta (d_{\mathrm{xy}})\) 各軌道のエネルギー準位を係数 A、B、C 及びスピン–軌道相互作用定数(\(\lambda\))で表わすと、
\[E_{\xi} = -\left[ \frac{B + C}{A} \right] \cdot \frac{\lambda}{2} \hspace{3mm}, \hspace{3mm} E_{\eta} = -\left[ \frac{C - A}{B} \right] \cdot \frac{\lambda}{2} \hspace{3mm}, \hspace{3mm} E_{\zeta} = -\left[ \frac{B - A}{C} \right] \cdot \frac{\lambda}{2} \tag*{[10]}\]となる。図19のエネルギー準位図でわかるように、エネルギー差 \(E \xi - E \eta\) はヘム平面内の歪み(\(\boldsymbol{R}\))による分裂を示している。\(g_{\mathrm{zz}} - g_{\mathrm{xx}}\) が増大する(即ち、\(g\) 値の異方性が増大する)とヘムの対称性が良くなる(分裂 \(R\) が小さくなる)ことが知られている。従って \(g\) 因子の異方性の変化からヘムタンパク質の軸配位子とヘムとの結合様式の変化を議論できる。また、種々の \(\ce{Fe^{3+}}\) 低スピン型ヘムタンパク質の \(g\) 値が詳細に解析されて、(\(\boldsymbol{\mu}\)、\(\boldsymbol{R}\))からヘム鉄に結合している配位子の種類、原子の種類を分類(予測)することができる(16)。
- \(\ce{N3^{-}}\) はヘム面法線に対して斜め方向に結合するため、ヘム面内の対称性が低下する。その結果 \(g\) 異方性は小さくなる。それに対し、\(\ce{CN^{-}}\) 結合型(シアノメト)では \(\ce{-C#N}\) が直線的にヘム垂直方向に向くので、ヘム面内の対称性が向上する。それゆえ、\(g\) 異方性は大きくなる(\(g_{\mathrm{z}} = 3.45\)、\(g_{\mathrm{x}} = 0.93\))。一方、ヘムの第5と第6配位座が His のイミダゾール基の場合(ビスイミダゾ-ル型)、2つのイミダゾール基面のなす角度がタンパク中で様々な立体障害を受けて変化する。2つの面の向きが直交するとき最も対称性が良く、\(g\) 異方性は大きくなり、\(g_{\mathrm{z}}\) 信号は低磁場側にシフトする。
- すべての \(g\) 因子の符号が常に正であるとはかぎらず、負になる場合もある。しかし、EPR のデータだけでは \(g\) 因子の正負は決められない。そこで、Bohan は \(g\) 因子の正負を含めた低スピン型ヘムタンパク質の EPR 解析法を提唱し、\(t_{\mathrm{2g}}\) 軌道のエネルギー準位を計算した(17)。
- 低スピン型ヘムタンパク質では \({g_{\mathrm{x}}}^{2} + {g_{\mathrm{y}}}^{2} + {g_{\mathrm{z}}}^{2}\) が16に近い値をとることが多い。これは、\((d_{\mathrm{xy}})^{2}(d_{\mathrm{xz}},{\ }d_{\mathrm{yz}})^{3}\) の電子配置である。ときたま、ヘムのモデルで \({g_{\mathrm{x}}}^{2} + {g_{\mathrm{y}}}^{2} + {g_{\mathrm{z}}}^{2}\) が14より小さい場合が(\(g\) 値の拡がりが小さい)報告されている。これは、\((d_{\mathrm{xy}})^{1}(d_{\mathrm{xz}},{\ }d_{\mathrm{yz}})^{4}\) の電子配置といわれている(18)。
② 低スピン型 \(\boldsymbol{\ce{Fe^{3+}}}\) ヘムタンパク質の EPR スペクトルを測定するときの問題点
以下に、低スピン型 \(\ce{Fe^{3+}}\) ヘムタンパク質の EPR スペクトルを測定するときの注意点を記述する。
- 試料濃度は高い方がやり易い。低スピン型のスピン数は \(S = 1/2\) なので、高スピン型(\(S = 5/2\))とは比較にならない程、EPR 信号強度は弱くなる。したがって、測定する試料の濃度を必然的に高くしなければ、良好な S/N 比をもつ信号は期待できない。高濃度に調整することが難しい試料もあるが、できれば最低でも 100 μM、100 μL は欲しい。もちろん、より低濃度でも測定はできるが、良好な S/N 比をもつ信号は期待できない。低濃度の場合は、データ積算回数を大幅に増やすことで S/N 比を向上できる。
- 測定温度は 15 K 前後がよい場合が多い。高スピン型では測定温度を低くする程、信号強度は増大したが、低スピン型では測定温度の設定には緩和時間の関係で注意が要る。\(\Delta g = g_{\mathrm{zz}} - g_{\mathrm{xx}}\) が狭い場合(第6配位子が\(\ce{OH^{-}}\)、\(\ce{N3^{-}}\)、P450 の低スピン種など)は 77 K でも測定できる。しかし、\(g\) 値の異方性が大きな分子種(第6配位子がイミダゾール、\(\ce{CN^{-}}\) など)では線幅増大、信号強度減少がおこり、77 K におけるスペクトル測定は難しい。この場合は、液体ヘリウムのフロークライオスタットを用いて 15 K で測定を行う。
- 5 K 前後の測定では、大抵の場合に信号強度は 15 K のときより低くなる。100 kHz 磁場変調で測定している場合は、スペクトルが歪む(吸収と分散が混ざる)ことがある。また、EPR 吸収のある範囲だけ特有のノイズが出ることもある。これらは、マイクロ波の飽和が原因である。従って、マイクロ波出力を下げるか、磁場変調周波数を低周波数に下げることになるが、信号強度は更に減少する結果になる。従って、一般には 15 K 付近での観測が望ましい。\(g\) 値の異方性が異常に大きな場合は、5 K~15 K の間で最適な温度条件を探す必要がある。
- 低スピン型 \(\ce{Fe^{3+}}\) ヘムタンパク質の EPR 信号はマイクロ波出力を高くすると飽和し易い。マイクロ波出力を変化させて、吸収に飽和が見られないかチェックをすること。
メモ
- \(g\) テンソル主値は、単結晶 EPR 解析を行って決定できる。しかし、経験的に溶液(凍結)試料の測定で得られる \(g\) 値を、\(g_{\mathrm{z}} > g_{\mathrm{y}} > g_{\mathrm{x}}\) の順に帰属して用いる(図17-C)。このように帰属する根拠として、Mb の単結晶を使って低スピン種の EPR を解析した結果がある。種々の軸配位子にについて、\(g_{\mathrm{z}}\) の向きはヘム面の法線(z 軸)にほぼ平行であること、\(g_{\mathrm{z}}\) 信号が最も低磁場側(\(g\) 値が最大)に、\(g_{\mathrm{x}}\) 信号が最も高磁場側(\(g\) 値が最小)に現れることが明らかにされている(21)。
③ 低温にすると低スピン型ヘムになるものがある
室温における光吸収スペクトル測定で \(\ce{Fe^{3+}}\) 高スピン型である試料について、低温で EPR スペクトルを測定すると、一部分が低スピン型 \(\ce{Fe^{3+}}\) ヘムタンパク質になっていることがある。この現象は、凍結による pH 変化等が原因による変性以外では、高スピン状態と低スピン状態の熱平衡に由来すると考えられる。
「凍結試料の電子状態は室温のそれと異なっているから、凍結試料を扱う低温の EPR 実験はタンパク質の構造と機能の相関を議論するには問題である」と考える人がいるかも知れないが、低温での測定結果には室温における構造・機能に関する情報が反映されている。(近年盛んに行なわれている低温における X 線結晶構造解析をどのように考えるか…)
- シトクロム P450cam を一例にとろう。基質カンファーが結合している場合、室温の光吸収スペクトルではほとんど高スピン状態である。しかし、凍結して 15 K で EPR 測定を行うと半分近くが低スピン状態(\(g_{\mathrm{z}} = 2.39\)、\(g_{\mathrm{y}} = 2.23\)、\(g_{\mathrm{x}} = 1.970\))である。酸化型 P450cam に電子供与体である鉄–イオウタンパク質(フェレドキシン、この場合はプチダレドキシン)の酸化型と 1 : 1 複合体を形成させると、P450cam の高スピン信号強度の減少と \(g_{\parallel}\) 分裂の増大(\(g_{\mathrm{x}} = 7.87\)、\(g_{\mathrm{y}} = 4.00\) → \(g_{\mathrm{x}} = 8.02\)、\(g_{\mathrm{y}} = 3.83\))が観測され、更に低スピン信号強度の増大と、\(\Delta g = g_{\mathrm{z}} - g_{\mathrm{x}}\) の僅かな増大(→ \(g_{\mathrm{z}} = 2.41\)、\(g_{\mathrm{y}} = 2.23\)、\(g_{\mathrm{x}} = 1.969\))が観測される。一方、基質カンファーが結合していない場合は完全に低スピン状態(\(g_{\mathrm{z}} = 2.42\)、\(g_{\mathrm{y}} = 2.23\)、\(g_{\mathrm{x}} = 1.910\))の EPR スペクトルを示す。このように、基質や電子供与体の結合によるヘム周辺の構造変化の情報が、EPR スペクトルに反映されている。
4-1-3 \(\boldsymbol{S = 5/2}\) と \(\boldsymbol{S = 3/2}\) が混合した中間スピン状態の EPR
ある種のヘムモデル錯体やヘムタンパク質では、\(g_{\perp}\) が6~4の間に観測されることがある。これは、\(S = 5/2\) と \(S = 3/2\) が混合した中間スピン状態の EPR 信号だと考えられている(22, 23)。ここで、中間スピン \(S = 3/2\) のみをもつ4重項状態 \(^{4}T_{1}\) が純粋な基底状態になる場合、その EPR 信号は理論的に \(g_{\perp} = 4\)、\(g_{\parallel} = 2.0\) に観測されるはずである。
スピン軌道相互作用によって \(S = 5/2\) の波動関数(\(\phi^{S = 5/2}\))と \(S = 3/2\) の波動関数(\(\phi^{S = 3/2}\))が量子論的に混ざり合う結果、\(S_{\mathrm{z}} = \pm 1/2\) に対する新しい波動関数 \(\Psi (\pm 1/2)\) は
\[\Psi(\pm 1/2) = a \phi^{S = 5/2} (\pm 1/2) + b \phi^{S = 3/2} (\pm 1/2) \tag*{[11]}\]で表される。外部磁場をヘム面に平行にかけた場合のゼーマン分裂より \(g_{\perp}⊥\) を計算すると、
\[g_{\perp} = 6a^{2} + 4b^{2} \tag*{[12]}\]となる。ここで、\(a\)、\(b\) は各波動関数の混ざりを示す係数で、\(a^{2} + b^{2} = 1\) を満足する。磁場をヘム面に垂直にかけると \(g_{\parallel} = 2.0\) である。係数 \(a^{2}\)、\(b^{2}\) から中間スピン \(S = 3/2\) 状態がどの程度混ざっているか判断できる。
- 低スピンヘムでは鉄原子はヘム面内に収まっており、高スピンヘムではヘム面から近位配位座側へとびだした構造をしている。混合中間スピン系のヘムではそれらの中間的な位置に鉄原子があると考えられる。
- 西洋ワサビペルオキシダーゼ(HRP)の酸化型の EPR スペクトルは \(g \sim 6\) 近傍に異方性を示す幾つかの成分がみられる。これらの異方性は使用する緩衝液の種類、pH で変化する。対応する一組の(\(g_{\mathrm{x}},{\ }g_{\mathrm{y}}\))の平均値(\((g_{\mathrm{x}} + g_{\mathrm{y}})/2\))は6より小さい値になる。HRP の EPR スペクトルから、\(S = 5/2\) の高スピン種に中間スピン状態 \(S = 3/2\) がかなり混ざっていることが示唆される。例えば、pH 7.0 のリン酸緩衝液の EPR スペクトルと異方性成分の多い pH 7.0 HEPES 緩衝液での EPR スペクトルの差スペクトルは、\(g_{\perp} = 5.3\) にひとつのピークを持つブロードで軸対称なスペクトル形状を示す(図20)。式 \([12]\) から、このスペクトルには約65%の \(S = 5/2\) 高スピン状態と35%の \(S = 3/2\) 中間スピン状態が混ざっていることが示される。
4-2 還元型ヘムタンパク質
EPR 分光法を使ったヘムタンパク質の電子状態の研究では、ヘム鉄が \(\ce{Fe^{3+}}\) であるさまざまな状態について、著しい成果を収めている。しかし、生理的にも重要である \(\ce{Fe^{2+}}\) ヘムの EPR による電子状態の研究はあまり進んでいない。\(\ce{Fe^{2+}}\) 高スピン(\(S = 2\))のような整数スピン系はクラマース2重項を持たないので(非クラマース2重項)、通常の EPR 測定が困難である。これは、\(\ce{Fe^{2+}}\) 低スピン(\(S = 0\))が反磁性であるため、磁気測定が出来ないことがその原因である。
4-2-1 高スピン型(\(\boldsymbol{S = 2}\))ヘムタンパク質の EPR
\(S = 2\) の系は、酸素分子の結合していない Hb や Mb(デオキシ Hb、Mb)が代表的な例である。この場合、スピン–軌道相互作用とゼーマンエネルギーの大きさが基底状態と励起状態のエネルギー差に較べて充分小さいとすると、量子力学的摂動論の取り扱いが可能となり、酸化型の場合と同様のスピンハミルトニアンを用いてゼーマンエネルギー準位の計算ができる。
計算の詳細は省略するが、スピンハミルトニアンの零磁場分裂定数 \(E \ne 0\) のとき、外部磁場をヘムの z 軸方向にかけ、マイクロ波磁界もその方向にかけると、非クラマース2重項 \(S_{\mathrm{z}} = \pm 2\) 準位間(\(\Delta S = 4\))での EPR 遷移の可能性が出てくる。Hendrich とDebrunner は、この条件を満足する特殊な EPR 共振器を用いて初めて還元型デオキシ Mb の EPR 測定に成功した(24, 25)。今後、詳しい電子状態の解析には、多周波数・強磁場 EPR 法によるデータ取得が必須である。そのため、測定装置の安定化、高感度化を目指す開発、研究が精力的に進められている。
- 還元型 \(\ce{Fe^{2+}}\) ヘムタンパク質の代わりとして、還元型 \(\ce{Fe^{2+}}\) ヘム鉄と同じ整数スピン(\(S = 2\))を持つ \(\ce{Mn^{3+}}\)–ポルフィリン置換ミオグロビン(\(\ce{Mn^{3+}Mb}\))を用いることで、「多周波数・強磁場EPR」測定を行うことができる。得られた EPR 信号解析により、零磁場分裂定数 \(D\)、\(E\) を正確に決定し、詳細なエネルギー準位を求めた(26)。
- 図21に \(\Delta S = 2,{\ }4\) の EPR 遷移を観測するため 10 GHz 帯の空洞共振器と実測例を示す。このような特殊な共振器は市販品がある(筆者は自作した共振器を使っている)。
4-2-2 低スピン(\(\boldsymbol{S = 0}\))のときは… 還元型 \(\boldsymbol{\ce{NO}}\) ヘムタンパク質の EPR
\(\ce{Fe^{2+}}\) 低スピン型ヘムタンパク質(酸素分子や一酸化炭素の結合した還元型へムタンパク質)は反磁性(\(S = 0\))なので、EPR 不活性種である。しかし、一酸化窒素(\(\ce{NO}\))は不対電子のスピン \(S = 1/2\) を持つので、\(\ce{NO}\) を還元ヘム鉄に結合させると \(g \sim 2\) を中心に独特の EPR スペクトルが観測される。この信号を観測することで、ヘムの配位構造が5配位か6配位かを区別できるほか、近位配位座の軸配位子を同定できるなど、ヘム近傍の構造が詳細に解析できる。従って、\(\ce{NO}\) 結合型ヘムタンパク質は、酸素結合型ヘムタンパク質のモデル系とも考えることできる。
① \(\boldsymbol{\ce{NO}}\) ガスの取扱
\(\ce{NO}\) ガスは無色の気体であるが、空気または酸素分子に触れると直ちに褐色の気体(\(\ce{NO2}\))に変化する。\(\ce{NO2}\) はアルカリ水溶液と作用して亜硝酸と硝酸またはその塩になるので、\(\ce{NO}\) ガスは 1 N \(\ce{NaOH}\) または \(\ce{KOH}\) 水溶液を通して \(\ce{NO2}\) を取り除いてから使用する。以下に、\(\ce{NO}\) ガスの取り扱い方についてまとめておく。
- 2 L 程度の耐圧瓶を準備する。この瓶の中に 1 N \(\ce{NaOH}\) または \(\ce{KOH}\) 水溶液を 500 mL 程入れる。
- 瓶の口径に合うゴム栓を準備し、大小2個の穴を開ける。大きい方の穴にはネジキャップセプタム付きのガラス管を差し込む。これは、ネジキャップ付き試験管の底を切り落とし、外径を少し細く細工することで用意する。もうひとつの小さい穴には、ガラス管またはポリエチレンチューブを差し込む。このガラス管(またはポリエチレンチューブ)の先にゴム風船を取り付ける。
- ゴム栓が加圧時に耐圧瓶から外れないように銅線などで瓶の口に固定する!
- 図8に示した真空ラインを用いて、瓶の中のアルカリ水を脱気し、\(\ce{N2}\) ガスで嫌気状態にする。(ネジキャップセプタムにさす注射針は太目のものを使うとよい)
- \(\ce{NO}\) ボンベと耐圧瓶をゴム管と注射針で繋ぎ、少しずつ \(\ce{NO}\) ガスを瓶の中に入れる。先ず、ストップバルブは閉めた状態で \(\ce{NO}\) ボンベ容器側のバルブを開ける。次に、ボンベ容器側のバルブを閉めてからストップバルブを開き、NOガスを嫌気瓶に導入する。ゴム風船が十分膨らむまで、この操作を繰り返す。この操作はドラフト内で行うことが望ましい。
- \(\ce{NO}\) ガスを取り出すときは、10~25 mL の気密性の良いガラス製シリンジを使う。注射針がロック出来ることが望ましい。はじめに、図9で示したようにシリンジ内部を嫌気洗浄する。次に、シリンジの注射針を \(\ce{NO}\)/\(\ce{N2}\) 混合ガスの入っている耐圧瓶のセプタムに差し込み、ゴム風船を軽く押してシリンジ内に \(\ce{NO}\)/\(\ce{N2}\) ガスを入れる(圧力でシリンジ内にガスが自然に入る)。
- 嫌気状態の還元型ヘムタンパク質が入っている試料管にシリンジ内の \(\ce{NO}\) ガスを注入する。EPR 試料管は細いので、\(\ce{NO}\) ガスを導入したのちに EPR 試料管上部を下に向けて指先で試料管を振動させ、試料管底部にある試料を試料管内壁に広げ、\(\ce{NO}\) が十分反応できるようにする。その後は氷中に暫らく放置する。\(\ce{NO}\) 結合型が不安定な場合は、できるだけ早く凍結測定する。空気が漏れていると大抵の場合、試料の沈殿がみられる。
- ゴム風船やゴム管などは \(\ce{NO}\) による腐食のため数日で使えなくなるので、取り換える。
② \(\ce{NaNO2}\) を使う方法
\(\ce{NO}\) ガスを使う代わりに、\(\ce{NaNO2}\) を酸化型ヘムタンパク質と反応させた後、嫌気条件下で還元する(ハイドロサルファイトなどで)と簡単に \(\ce{NO}\) 結合型ヘムタンパク質ができる。\(\ce{^{15}NO}\) は同位体ガスとして購入できるが、\(\ce{Na ^{15}NO2}\) を使う方が実験はやり易い。
メモ
③ \(\boldsymbol{\ce{NO}}\) 結合型ヘムタンパク質の EPR スペクトルの実際
\(\ce{NO}\) 結合型ヘムタンパク質は大きく分けて2通りに分類できる。すなわち、5配位構造と6配位構造である。これらを順に説明する。
- 5配位構造とは、\(\ce{NO}\) が配位することでタンパク質本来の第5配位座(近位)の配位子とヘム鉄との結合が切れた構造のことである。このときの EPR スペクトルは、\(g_{\mathrm{z}} = 2\) に \(\ce{^{14}NO}\) の核スピンによる特徴的な3本の hfs 分裂(\(\ce{^{15}NO}\) の場合は2本の hfs 分裂)信号を示す(図22-A)。これが、\(\ce{NO}\)–ヘム鉄が「5配位構造」を示す典型的なスペクトルである。一般に、\(g_{\perp} (g_{\mathrm{x}}\text{、}g_{\mathrm{y}})\) に異方性 \(g\) 値の分裂がみられるが、\(g_{\perp} > g_{\mathrm{z}}\) という特徴をもっている。
メモ
- 6配位構造とは、\(\ce{NO}\) とタンパク質本来の第5配位座の配位子が、ヘム鉄が結合している構造のことである。この構造は \(g\) 異方性を示し、\(g_{\mathrm{x}} > g_{\mathrm{z}} > g_{\mathrm{y}}\) の順になる。EPR スペクトルの例を図22-Bに示す。第5配位座の配位子が N 核を持つヒスチジンなどの場合は、\(\ce{^{14}NO}\) の \(\ce{^{14}N}\) で3本に分裂した信号が His の \(\ce{^{14N}}\) 核で更に3本に分裂し、9本の hfs 分裂が観測される。\(\ce{^{15}NO}\) を配位させた場合は、2本の \(\ce{^{15}NO}\) による分裂が更に3本ずつに分裂し、計6本に分裂する。第5配位子が N 核を待たない場合(例えば P450)、\(\ce{NO}\) の hfs 分裂が更に分裂することはない。通常の \(\ce{^{56}Fe}\) ヘム鉄では核スピンが \(I = 0\) であるため、\(\ce{Fe}\) 核による分裂は見られない。ヘム鉄を \(\ce{^{57}Fe}\) に置換すると、\(\ce{^{57}Fe}\) の核スピン \(I = 1/2\) によって \(\ce{NO}\) の信号が更に2本ずつに分裂する。\(\ce{^{56}Fe}\)、\(\ce{^{57}Fe}\) 置換 \(\ce{NO}\) 結合型ヘムタンパク質の EPR スペクトルの比較することにより、\(\ce{NO}\) が還元型ヘム鉄に結合していることが保証される(図22)。
④ 測定温度
- \(\ce{NO}\) 結合型ヘムタンパク質の EPR 測定のひとつの利点は、十分な試料濃度があれば、室温での測定ができることである。これにより、室温に於ける他の分光学実験、生化学実験の結果と比較して議論することができる。
- 室温での測定は濃度が必要であるため、低濃度の試料の測定は低温で行わざるを得ない。77 K での測定が最も容易であるが、\(\ce{N2}\) の気泡による S/N 比の低下を考えると、フロークライオスタットを用いて 30 K 前後で測定するのが望ましい。この場合は、77 K での測定よりはるかに薄い試料濃度で S/N 比の良いスペクトルが得られる。
- 装置の性能にも依存するが、100~200 μM 程度の試料濃度がある方が S/N 比の良好なスペクトルが得られる。もちろん、もっと低濃度でも測定は可能で、S/N 比を向上させるには積算回数を多くすればよい。
- \(\ce{NO}\) 結合型の EPR スペクトルには複雑な hfs 分裂がある。そのため、スペクトルの変形を防ぐために、低マイクロ波出力でかつ低磁場変調幅で測定を行う必要がある。
4-3 EPR 不活性分子種を EPR 活性化する
EPR を用いたヘムタンパク質の研究の対象は、半整数スピン(\(S = 5/2\)、\(S = 1/2\))を持つ \(\ce{Fe^{3+}}\) 状態が主であった。生理的に重要であり、整数スピン系ヘム鉄(\(S = 2\))を持つ還元型 \(\ce{Fe^{2+}}\) ヘムタンパク質のヘム鉄の電子状態については、十分な知見が得られていない。そこで、\(\ce{Fe^{3+}}\) や \(\ce{Fe^{2+}}\) 以外で EPR 観測が可能な金属(表1参照)を鉄の代わりに用いた金属置換ヘムタンパク質を再構成し、\(\ce{Fe^{2+}}\) ヘムタンパク質のモデルとする研究が積極的に行なわれている。金属置換体の EPR スペクトル解析から、中心金属イオンと周辺アミノ酸残基との相互作用を解明できる。
4-3-1 コバルト(\(\boldsymbol{\ce{Co^{2+}}}\))置換ヘムタンパク質
\(\ce{Co^{2+}}\)(\(3d^{7}\)、\(S = 1/2\))錯体は可逆的に酸素分子と結合することが知られている。従って、\(\ce{Co^{2+}}\) 置換体は、ヘムタンパク質の酸素分子結合型を研究する際のよいモデルとして研究されている。
\(\ce{Co^{2+}}\) 置換体を作成するには、先ず、\(\ce{Co^{2+}}\)–ポルフィリンを合成するか購入する。次に、対象とするヘムタンパク質からヘムを抜いたアポタンパク質を調整する。さらに、アポヘムタンパク質に \(\ce{Co^{2+}}\)–ポルフィリンを入れ、\(\ce{Co^{2+}}\)–置換ヘムタンパク質を再構成する。\(\ce{Co}\) の核スピンは \(I = 7/2\) であるので、\(\ce{Co}\) 核の shfs(超超微細構造)分裂が8本みられる。
- 酸素分子の配位した \(\ce{Co^{2+}}\) は、電子論的には \(\ce{Co^{3+}-O2^{-}}\) と考えられている。従って、\(\ce{O2^{-}}\)(スーパーオキシド)に対応する軸対称な EPR スペクトル(\(g_{\parallel} > g_{\perp}\))が \(g = 2\) 近傍に現れる。この信号は室温でも観測できるが、S/N 比の良いスペクトルを得るには低温測定が必要である。室温と低温では、EPR スペクトルに配位子 \(\ce{O2^{-}}\) の運動による影響がみられるので、解析には注意が必要である。
- 酸素分子の結合していないデオキシ型 \(\ce{Co^{2+}}\)–置換ヘムタンパク質のスピン数は、酸素結合型と同じ低スピン型 \(S = 1/2\) であるが、\(g_{\perp} = 2.3\)、\(g_{\parallel} = 2.0\) に5配位型 \(\ce{Co^{2+}}\) ポルフィリンの特徴を示す軸対称スペクトルを示す。\(g_{\parallel}\) の信号は、\(\ce{Co}\) 核の核スピン(\(I = 7/2\))で8本に分裂する。軸配位子(第5配位子)が核スピンをもつ場合、例えば His では \(\ce{^{14}N}\) 核の核スピンは \(I = 1\) であるので、これらの信号が更に3本ずつに分裂する。ヘム面の対称性が悪くなると \(g_{\perp}\) 信号の分裂、線幅増大が観測される。
4-3-2 他の金属置換ヘムタンパク質の EPR
\(\ce{Co^{2+}}\) 以外にも、表-1に示したような EPR 活性な \(3d\) 遷移金属(\(\ce{Mn^{3+}}\)、\(\ce{Mn^{2+}}\)、\(\ce{Cu^{2+}}\)、\(\ce{VO^{2+}}\) など)をポルフィリンに導入した金属置換ポルフィリンの合成がなされている。これらの金属置換ポルフィリンをアポタンパク質に入れ、金属置換再構成ヘムタンパク質をつくることで、さまざまな応用研究がなされている。
- \(\ce{Cu^{2+}}\) や \(\ce{VO^{2+}}\) 置換ポルフィリンで再構成したヘムタンパク質では、室温の EPR 測定も可能である(27)。
- \(\ce{Mn^{3+}}\) 置換ポルフィリンはデオキシヘム鉄(\(\ce{Fe^{2+}} : S = 2\))のモデルタンパク質として、電子状態の研究で重要な役割を果たしている。
- \(\ce{Cu^{2+}}\) は金属置換ヘムタンパク質への応用よりは、本来の銅タンパク質として活性中心の \(\ce{Cu^{2+}}\) 錯体の EPR 解析が重要になる。配位構造についてヘムタンパク質と同様の議論ができるが、ここではこれ以上は触れない(28, 29)。
- \(4d\) に不対電子を持つモリブデン(\(\ce{Mo}\))もキサンチン酸化酵素、ニトロゲナーゼなどの酵素において、活性中心金属として重要な役割を演じている。通常、EPR で観測されているのは \(\ce{Mo(V)}\) の状態である。天然に存在する \(\ce{Mo}\) には7種類の同位体がある。\(\ce{^{95}Mo}\) と \(\ce{^{97}Mo}\) は核スピン \(I = 5/2\) をもち、これらの \(\ce{Mo(V)}\) 錯体では6本の hfs が観測される(30)。
4-3-3 スピン・スピン交換相互作用の強さを変えて EPR を観測する
酸化型ヘムタンパク質(\(S = 5/2\)、\(1/2\))は「EPR 活性」であるが、一酸化窒素(\(S = 1/2\))が結合すると「EPR 不活性」になる。しかし、この状態を以下のように活用することで、ヘム周辺のアミノ酸残基の立体構造に関する詳しい情報を得ることができる。
EPR 不活性な \(\ce{NO}\) 結合型を極低温下で可視光照射すると、解離した \(\ce{NO}\) がヘム遠位空間にトラップされ、\(S = 5/2 \leftrightarrow S = 1/2\) スピン系の特異な EPR 吸収が観測される。ここで、遠位ヘム空間のアミノ酸側鎖が立体障害になり、\(\ce{NO}\) がヘム鉄に近い位置にトラップされると、スピン・スピン交換相互作用による特異な EPR 吸収が現れる。一方、アミノ酸側鎖による立体障害が少ないと、\(\ce{NO}\) 分子はヘム鉄からかなり離れたところまで移動し、磁気双極子相互作用による信号の線幅増大を引き起こす。このように、低温における \(\ce{NO}\) 配位型ヘムタンパク質の光解離実験を行うことで、ヘム周辺のアミノ酸残基の立体構造を議論することが出来る(31)。酸化型 Mb–\(\ce{NO}\) の光照射実験の結果を図23にまとめてみた。
- 酸化型ヘムタンパク質に対する \(\ce{NO}\) の親和性は一般に低い。従って、\(\ce{NO}\) 型を作るためには、酸化型ヘムタンパク質に対して大過剰の \(\ce{NO}\) ガスを嫌気状態下(窒素雰囲気)で注入する。茶褐色の酸化型ヘムタンパク質溶液が、\(\ce{NO}\) 結合によってピンク色に変わることが観測される。しかし、十分に \(\ce{NO}\) を結合させようとするあまり、長時間氷中に放置しすぎると、ヘム鉄の還元(一部 \(\ce{Fe^{2+}}\)–\(\ce{NO}\) になる)とタンパク質の変性がおこる。
- \(\ce{Fe^{3+}}\)–\(\ce{NO}\) 型の試料では、EPR スペクトル上には \(g = 2\) 近傍の free \(\ce{NO}\) の吸収以外はなにも観測されない。この状態になったことを確認した後、50~150 W 程度のスライドプロジェクター光をレンズで集光して、空洞共振器の外側から測定試料に照射する。光照射時間は EPR スペクトルの結果で判断する。
- 光照射は極低温で行うと、データの解釈が容易である。例えば、光照射を 5 K で行ったとする。光照射後に EPR スペクトルを観測し、次に試料の温度を上げてから、再び 5 K に戻して EPR スペクトルを測定する。温度を上げることによって、一旦光解離した \(\ce{NO}\) が、ヘム鉄に再結合する過程の情報が得られる。
- 呼吸鎖末端酸化酵素の酸化型酵素の「\(\ce{Fe^{3+}}\) ヘム(\(S = 5/2\))–\(\ce{Cu_{B}}\)(\(S = 1/2\))」複核中心は \(S = 5/2 \leftrightarrow S = 1/2\) スピン・スピン交換スピン系を持っている。これは、電子論的には \(\ce{Fe^{3+}}\)–\(\ce{NO}\) 光解離型分子種と類似しており、同様な EPR スペクトルを示す。
4-4 非ヘム鉄タンパク質の EPR
生体内での鉄錯体は \(\ce{Fe}\)–ポルフィリン(いわゆるヘム鉄)と、非ヘム鉄に分類できる。非ヘム鉄タンパク質としては、鉄–硫黄タンパク質(フェレドキシン)が代表的であり、\(\ce{Fe}\)–\(\ce{S}\) 複核中心が活性部位を形成している。このほか、さまざまな鉄錯体が知られており、EPR を使った良い研究対象である。ここでは、\(\ce{Fe}\)–\(\ce{S}\) 複各中心を持つタンパク質を中心に、EPR データや測定時の特性をまとめる。
4-4-1 鉄–硫黄タンパク質を分類すると
鉄–硫黄タンパク質の中にも、さまざまな種類が存在する。特に、EPR 観測の視点からこれらのたんぱく質の分類を行う。
- 1個の鉄原子に4個のシステイン(Cys)残基の \(\ce{S}\) 原子が結合しているルブレドキシンは酸化型において高スピン \(S = 5/2\) 由来の \(g = 4.3\) に EPR 吸収を示す。還元型は EPR 不活性でなる。
- 2個の鉄原子が2個の硫黄原子と結合した \(\ce{2Fe}\)–\(\ce{2S}\) 複核中心を持つフェレドキシンも知られている。この場合、二つの鉄原子に4個の Cys 残基のS原子が結合して活性部位を形成する。酸化型は EPR 不活性である。1電子還元した(例えば、嫌気条件下でハイドロサルファイトを加える)還元型では、\(g = 2\) 付近に特有の信号を示す(\(g_{\parallel} > g_{\perp}\))。この信号は、鉄原子の一方のみが還元されて、高スピン状態の酸化型鉄(\(S = 5/2\))と高スピン状態の還元型鉄(\(S = 2\))間の反強磁性相互作用による見かけ上のスピン \(S'= 1/2\) で説明できる。このタイプに属する植物フェレドキシン(例えば、ホウレン草フェレドキシン)では \(g_{\perp}\) に分裂がみられる。副腎フェレドキシン(アドレノドキシン)やプチダレドキシンでは軸対称な EPR スペクトルを示す。
- 4個の鉄原子と4個の硫黄原子が \(\ce{4Fe}\)–\(\ce{4S}\) 複核中心を作り、さらに、複核中心の鉄原子と4個の Cys 残基の \(\ce{S}\) 原子が結合して活性部位を形成しているタンパク質もある。\(\ce{2Fe}\)–\(\ce{2S}\) 複核中心の場合と同様に、\(\ce{Fe}\)–\(\ce{Fe}\) 間には反強磁性相互作用が働いている。1電子還元で \(g = 2\) 付近に特有の信号を示す(\(g_{\parallel} > g_{\perp}\))。
- \(\ce{4Fe}\)–\(\ce{4S}\) 複核中心の4個の \(\ce{Fe}\) 原子のなかの1個が抜けて、\(\ce{3Fe}\)–\(\ce{4S}\) 複核中心が形成される場合もある。この試料を1電子還元すると、測定温度 5 K で零磁場近傍に \(S' = 2\) 由来の特異な幅広い信号が観測される。この信号は \(\ce{Fe^{3+}}\)–\(\ce{NO}\) ヘムタンパク質の光解離型や \(\ce{Fe^{3+}}\) ヘム鉄–\(\ce{Cu_{B}}\) 複核中心に類似している。
4-4-2 測定温度
鉄–硫黄タンパク質の EPR スペクトルは 77 K で測定できるものも多いが、15 K 前後で測定する方が試料濃度を低くすることが可能であり、S/N 比の良いスペクトルが得られる。飽和しやすいのでマイクロ波出力は低く抑えた方が良い結果が得られる。
5. 短寿命反応中間体の捕捉とEPR測定
生体化学反応は酵素と基質を混合することで開始される。そのため、短寿命反応中間体の EPR スペクトルの測定のためには、短時間内に酵素と基質を混合し中間体分子種を捕捉する必要がある。反応中間体を観測するために、大きく分けて2つの実験方法が知られている。
5-1 連続流通法
この手法では、短寿命のラジカルの生成と消滅過程を室温で観測する。シリンジ内の酵素溶液と反応液(基質)をガス駆動で混合セル(ミキサー)に導入し、反応混合液を連続的に押し流しながら空洞共振器内の EPR 試料管内を通過させてEPRを観測する。測定は室温であるから、試料管は毛細管ないしは扁平型試料管になる。ミキサーとEPR測定部との距離や反応液の流速を変えることで、反応後のラジカル信号の時間変化が追跡できる。
5-2 急速混合凍結法
この手法では、はじめに液体窒素やイソペンタン寒剤の中にミキサー部から噴出する反応混合液を注入して瞬時に凍結し、反応を停止させる。次に、凍結反応物を EPR 試料管に詰めて EPR スペクトル測定を行う。測定温度は当然、極低温になる。この場合、EPR 活性な反応中間体と未反応ヘムタンパク質が同時に測定される。また、混合凍結時間を変えることで反応の時間変化を追跡できる。
本稿では、急速混合凍結法によるヘムタンパク質の反応中間体の捕捉、EPR 測定について具体的な測定例を紹介する。
5-2-1 ペルオキシダーゼと過酸化水素の反応
酸化型西洋ワサビペルオキシダーゼ(HRP)と過酸化水素(\(\ce{H2O2}\))との反応を例にとる。この反応で、最初に形成すると考えられている反応中間体は、\(\ce{Fe^{3+}}\)–ヘムに \(\ce{H2O2}\) が結合した \(\ce{Fe^{3+}}\)–\(\ce{H2O2}\) である(Compound 0 と呼ばれる)。この状態は、電子論的には \(\ce{Fe^{3+}}\)–\(\ce{O2^{2-}}\) のパーオキシド型 \(\ce{Fe^{3+}}\) 低スピン分子種と等価であり、\(\ce{Fe^{3+}}\) 低スピン型の EPR スペクトルを示すはずである。しかし、HRP では、200 μs の急速混合凍結実験でもこの中間体は捕捉できない。
① HRP Compound I の試料調整
HRP と \(\ce{H2O2}\) の反応で実際に観測される中間体は、いわゆる Compound I と呼ばれる \(\ce{Fe^{4+}=O}\)/ポルフィリンπカチオンラジカルである。この試料の極低温下における EPR スペクトルには、特異なラジカル信号が存在する。\(\ce{Fe^{4+}=O}\) は \(S = 1\) であるため EPR 信号は観測されないが、\(S = 1\) とポルフィリンπカチオンラジカル(\(S = 1/2\))とのスピン・スピン交換相互作用による信号として説明できる。この状態の観察のためには、以下のような実験手順をふむとよい。
- ポリエチレンチューブで作製した自在型ピペットを用いて酸化型 HRP(例えば濃度 200 μM、試料体積 25 μL)を EPR 試料管の底部に注入する。
- EPR 試料管の試料位置より 1~2 cm上部に1~2等量の \(\ce{H2O2}\) を自在型ピペットで注入する。このとき、\(\ce{H2O2}\) が HRP と混ざらないようにする。試料管を横に向ければやり易い。
- EPR 試料管の上部にゴムキャップを付けて封じておくことを忘れないこと。ゴムキャップを付ける際に \(\ce{H2O2}\) が HRP 側に押し込まれないように注意する。
- 金属製デュワー瓶に液体窒素かイソペンタン寒剤(100~150℃)を用意しておく。前述したように、イソペンタン寒剤の方が試料凍結時間は早い。
- EPR 試料管を一気に振り下ろし、同時に寒剤の中に素早く挿入する。試料管内の酸素分子の影響が気になる場合は、試料管をイソペンタン寒剤に入れた状態で、上部のゴムキャップから図8で示したやり方で試料管内のガス交換を行えばよい。
- 液体窒素の入ったデュワー瓶に EPR 試料管を移してから極低温での EPR 測定を行う。
② HRP Compound I の EPR スペクトル
HRP Compound I の測定例を図24に示す。使用する緩衝液の種類で信号の形が異なっていることに注意して欲しい。マイクロ波出力の依存性を測定することが望ましい。Compound I は 5 K でも飽和し難い。
5-2-2 サブミリ秒領域での反応中間体の捕捉と EPR 測定
HRP Compound I の測定の際に用いた急速混合凍結法は反応が比較的遅く、反応中間体の寿命もかなり長い(安定)場合、反応中間体を捕捉する方法として有効である。しかし、この手法では、混合してから凍結するまでの時間を正確に決めることはできない。一方で、サブミリ秒以下で酵素反応中間体を捕捉し、EPR 測定を行う実験は非常に難しい。
急速凍結装置として従来から知られている手法では、不感時間帯が約5ミリ秒以上もあるため、サブミリ秒領域における高速生体反応の計測は全くできなかった。しかし、大阪大学蛋白質研究所の高橋らが設計・作製した急速溶液混合凍結装置では、溶液の混合から凍結まで最速時間200マイクロ秒を可能にした(32)。図25に急速溶液混合凍結装置の概略図を示す。
以下に、この急速混合凍結装置を用いた試料調整と EPR 測定の手順等について述べる。
① 装置の動作原理
本装置の特徴は流路内径 60 μm φ のミキサー部分とミキサーより噴出した反応混合液(噴霧状液体)を液体窒素温度(77 K)と平衡にある銀製回転ディスク面(ローラー)にぶつけて、瞬時に凍結させるところにある。凍結されたフレーク状の反応物は、液体窒素デュワー底に溜る。理論的には、反応時間 \(\boldsymbol{t}\) は \(\boldsymbol{t = X/V}\) で与えられる。
- \(\boldsymbol{X}\) はミキサーと銀製回転ディスクとの距離で、通常は 1 cm を使う。\(\boldsymbol{V}\) は反応液の流速で流量をミキサーの噴出穴の断面積で割った値である。したがって、ミキサー部の流路内径を 60 μm φ より細くする事が出来れば、もっと速い混合凍結時間の実験が可能になる。しかし、流路内径を小さくするとミキサーが沈殿物などで詰まり易くなる。詰まった場合は、ミキサー部を分解してミキサープレートを超音波洗浄する。
- 液体窒素中の銀製回転ディスク面とミキサー噴出口との距離 \(\boldsymbol{X}\) を短くすればする程、速い凍結時間が得られることが理解できる。しかし、低温で回転しているディスクに近づけ過ぎるとミキサーの噴出口が凍ってしまう危険性がある。
② 装置の改良
高橋らが製作したオリジナルの装置では、2つのパイレックス製シリンジに入っている反応液をシリンジピストン駆動モーターで押し出す方法をとっていた。また、流路はテフロンチューブを使用していた。しかし、高速反応実験をする場合に、シリンジピストン駆動モーターにかなりの負荷がかかり、空回りなどで反応時間の再現性がよくなかった。そこで、シリンジピストン駆動モーター方式を高速液体クロマトグラフィー HPLC のポンプにとり替えて、一定の流量が確保できるようにしたところ、再現性の良い結果が得られた。
- HPLC ポンプの最大流量に耐えられるように、テフロンチューブの代わりにテフゼルチューブ(Ethylene Tetrafuluoro Ethylene 内径 × 外径 = 0.5 mm φ × 1.58 mm φ)を使う。圧力負担のかかり易い各流路のコネクター部分は耐圧性の良い PEEK(Poly Ether Ether Ketone)材質に切り替えた。
③ 凍結試料の回収
液体窒素デュワー底に溜っているフレーク状の反応物をスパチュラ(予め液体窒素で冷やしておく)で液体窒素と一緒にすくい、細長い液体窒素ガラス製デュワー瓶(内部が見えるようにスリットがある)中の EPR 試料管に少しずつ入れる。EPR 試料管内のフレーク状反応物は試料管内径に合わせたアクリル丸棒で試料管底に押し固める。
④ 凍結試料の脱気
−150℃に調整したイソペンタン寒剤を用意する。この寒剤の中にアクリル丸棒を入れたままの試料管を液体窒素デュワーから移す。アクリル棒を静かに抜き取り、EPR 試料管にアメゴム付きのキャップを閉める。さらに、図8のやり方で試料管内の固体酸素を気化させ、除去する。この試料をEPR測定となる。
⑤ 凍結試料回収時の工夫
凍結時間にムラがあると、凍結標品の大きさにムラが生じ、凍結時間が遅い程大きくなる。大きなフレーク(大抵は液体窒素中に浮遊している)は捨てなければならない。一方で、高速の凍結時間の場合には、凍結票品は非常に細かいフレーク状になるが、静電気などでなかなか試料管に試料を移動させることができない。そのため、EPR試験管に効率よく詰める幾つかの方法が考案されている(図25 下図)。
⑥ 凍結時間の較正
混合凍結時間の較正には、アコメト Mb と \(\ce{N3^{-}}\) の結合反応を用いる。
結合速度定数を \(k\) とすると、\(\ce{NaN3}\) の濃度がアコメト Mb の濃度に対して過剰量なので、疑一次反応速度で扱える。すなわち、
\[k = 7.0 \times 10^{3}{\ }\mathrm{s}^{-1}{\ }\mathrm{M}^{-1} \hspace{3mm} \text{(pH 7.0) を用いて、} \hspace{3mm} t = \ln \{ (1 - a)^{-1} / (k \mathrm{[NaN_{3}]}) \} \tag*{[13]}\]となる。ここで、\(a\) は \(\ce{N3}\) 結合型 Mb の割合で、完全アコメト型 Mb と完全 \(\ce{N3}\) 結合型 Mb の EPR スペクトルより計算される。得られた \(a\) と \(\ce{NaN3}\) 濃度を代入して反応時間 \(t\) が求まる。\(k\) は pH で大きく変化するので、試料の pH 調整には注意が要る。
メモ
6. おわりに
多くの研究室で使用されている普通の 10 GHz 帯の CW-EPR 装置を使って、金属タンパク質とりわけヘムタンパク質を測定する際に参考になると思われる基本的な実験技術、注意事項、裏ワザなどを思いつくままに書いてみた。書き足らない事項も多々あり、まとまりのない文章になってしまったかもしれない。実験をされるときに必要なところだけ読めば実験の手助けになるようには書いたつもりである。参考にして頂ければ幸いである。最近のパルス EPR 法を使われる場合でも、本稿で述べた基本的な測定試料取扱の技術は生きてくるものと信じている。
本稿をまとめる機会を与えて下さった大阪大学蛋白質研究所の高橋 聡氏、貴重なコメントを頂いた東北大学多元物質科学研究所の齊藤 正男氏に感謝致します。
7. 参考文献
- Pake, G. E. 著(出口安夫ほか訳)「常磁性共鳴」(化学同人)
- Slichter, C. P. 著(増田義賀、雑賀亜幌訳)「磁気共鳴の原理」(岩波書店)
- 石津和彦編 「実用ESR入門 ― 生命科学へのアプローチ」(講談社サイエンティフィク)
- Alger, R. S. 著(磯部太郎監訳、岩泉正基ほか訳 「電子スピン共鳴 ― 実験技術とその応用 ― 」(吉岡書店)
- 廣田鋼藏 編集 日本化学会編 実験化学講座 続13「電子スピン共鳴」(丸善)
- Andersson K. K., et al., J. Biol. Inorg. Chem., 8, 235–247 (2003)
- Schünemann V., et al., J. Biol. Chem., 279, 10919–10930 (2004)
- Miyajima Y., et al., J. Phys. Soc. Japan, 73 280–286 (2004)
- Froncisz, W., and Hyde, J. S., J. Magn. Reson., 47, 515–521 (1982)
- Orii Y. and Morita M., J. Biochem., 81, 163–168 (1977)
- Sands, R. H., Phys. Rev., 99, 1222–1226 (1955)
- Kneubühl, F. K., J. Chem. Phys., 33, 1074–1078 (1960)
- Gibson, J.F., and Ingram, D. J. E., Nature, 180, 30–31 (1957)
- Griffith, J. S., Nature, 180, 30–31 (1957)
- Taylor, C. P. S., Biochim. Biophys. Acta, 491, 137–149 (1977)
- Harris Loew, G. M., Biophys. J., 10, 196–212 (1970)
- Bohan, T. L., J. Magn. Reson., 26, 109–118 (1977)
- Walker, F. A., et al., J. Am. Chem. Soc., 118, 12109–12118 (1996)
- Blum, H., Leigh, J. S., and Ohnishi, T., Biochim. Biophys. Acta, 626, 31–40 (1980)
- Blum, H., et al., J. Biol. Chem., 256, 2199–2206 (1981)
- Hori, H., Biochim. Biophys. Acta, 251, 227–235 (1971)
- Maltempo, M. M., et al., Biochim. Biophys. Acta, 342, 290–305 (1974)
- Maltempo, M. M., J. Chem. Phys., 61, 2540–2547 (1974)
- Hendrich, M. P., and Deburunner, P. G., J. Magn. Reson., 78, 133–141 (1988)
- Hendrich, M. P., and Deburunner, P. G., Biophys. J., 56, 489–506 (1989)
- Horitani, M. et al., J. Inorg. Biochem., 102, 781–788 (2008)
- Shibayama, N., et al., FEBS Lett., 372, 126–130 (1995)
- Malmström, B., et al., Biochim. Biophys. Acta, 205, 48–57 (1970)
- Dawson, J. H., et al., Proc. Natl. Acad. Sci. U.S.A., 75, 4078–4081 (1978)
- Bray, R. C., and Meriwether, L. S., Nature, 212, 467–469 (1966)
- Hori, H. et al., J. Inorg. Biochem., 82, 181–187 (2000)
- Tanaka, M., et al., Biophys. J., 84, 1998–2004 (2003)
- Kumita, H., et al., J. Biol. Chem., 279, 55247–55254 (2004)
これらの参考書の多くは古く、原著や訳本の入手は難しいかも知れないが、大学図書館の蔵書には必ずあると思う。特に、1) と2) は磁気共鳴の教科書として必読書である。また、4) については測定装置に関する重要な教科書である。
-
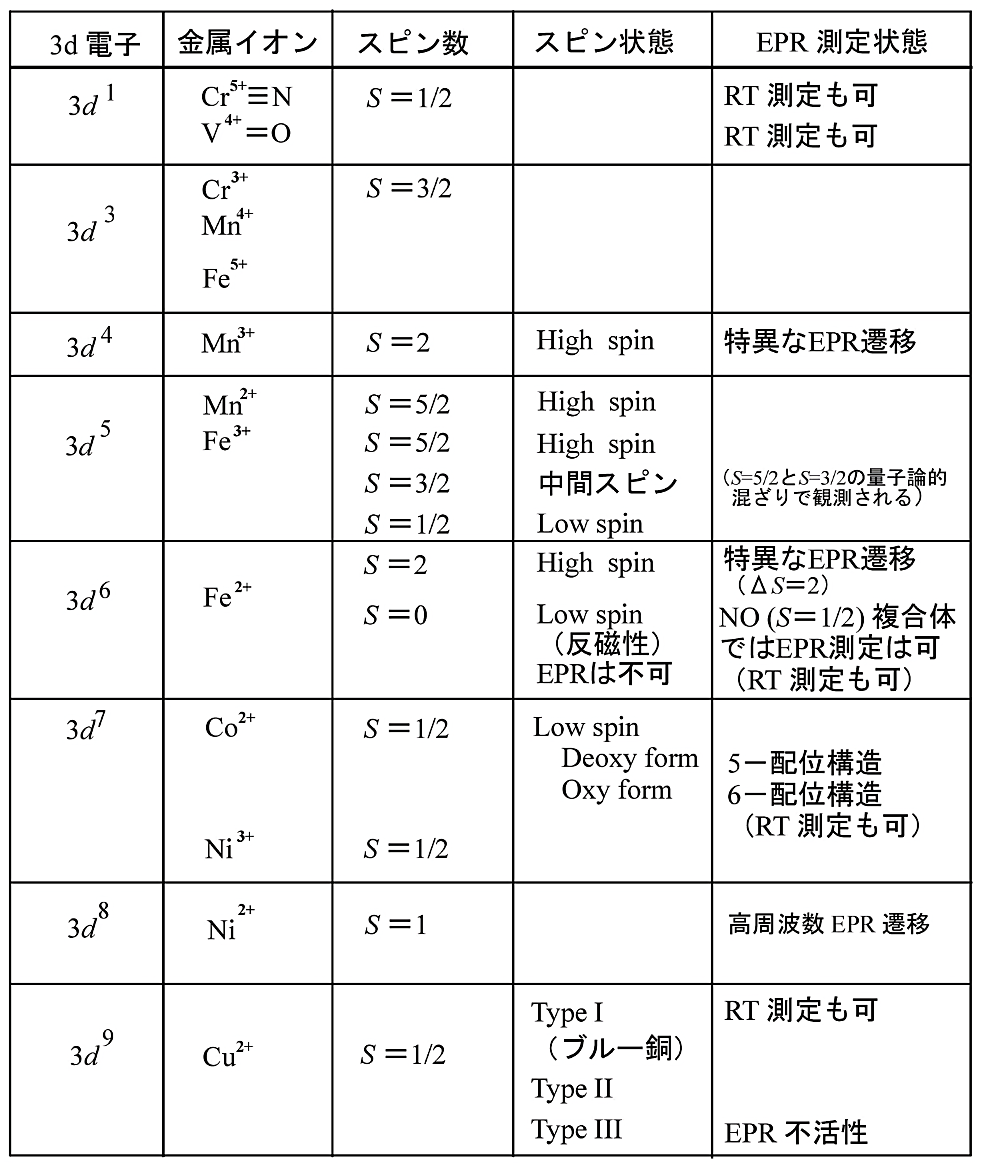
表1:EPR 測定可能な \(3d\) 遷移金属イオン
EPR 活性(測定可能)な金属は各 \(3d\) 金属イオンのスピン状態、酸化状態で異なるが、特別な遷移(\(\Delta S = 2\) など)を除けば、通常は半整数スピン系スピン間の遷移(\(\Delta S = 1\))を測定対象とする。 -
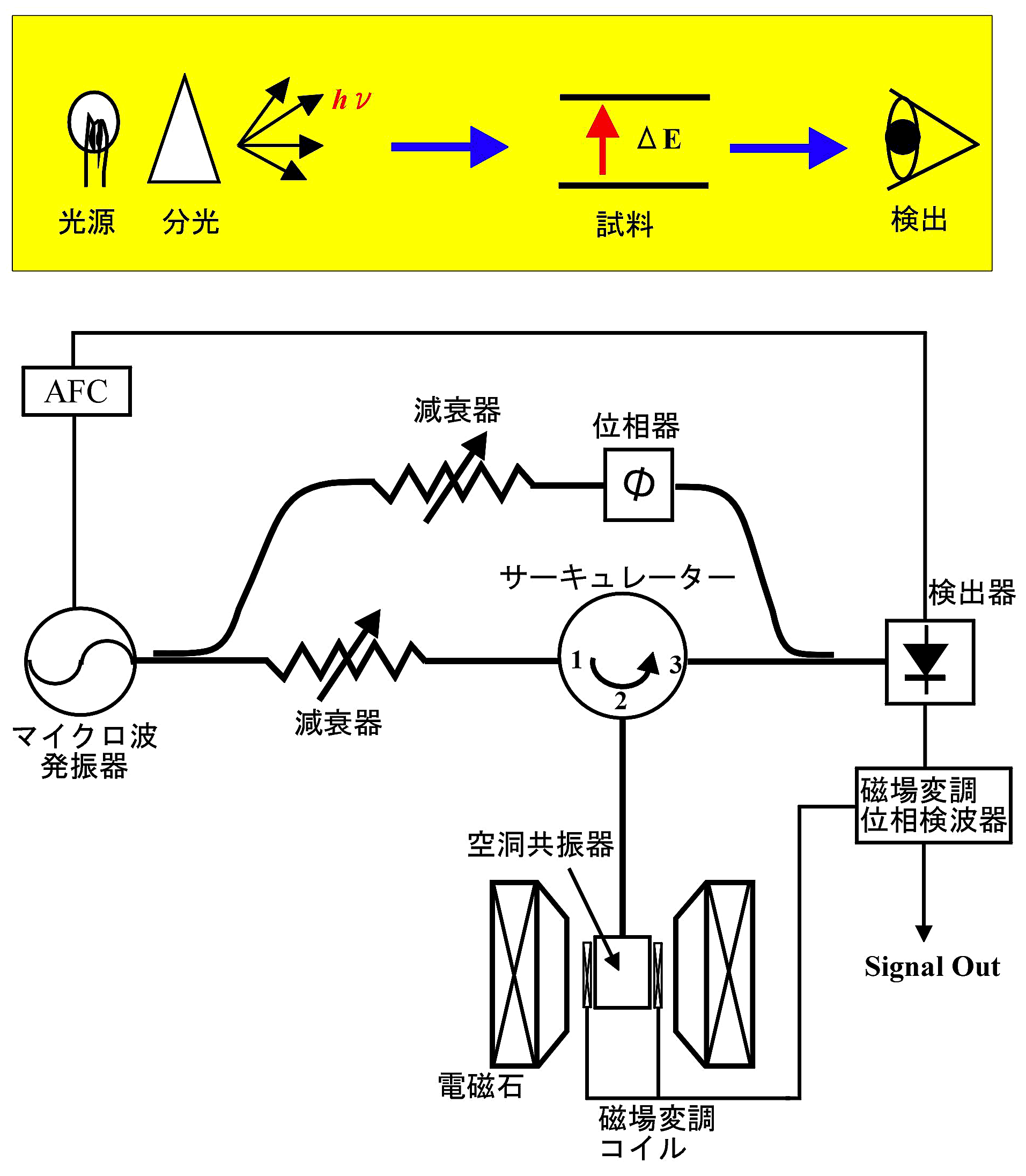
図1:分光測定法の原理図(上図)と EPR 装置のブロック図(下図) -
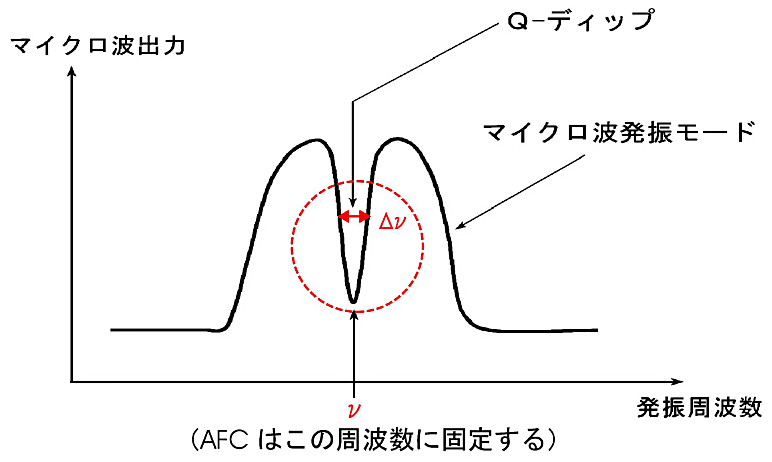
図2:Q-ディップ
共振器の共振の鋭さを示す量として Q 値が用いられる。
共振周波数 \(\nu\) と共振の半値幅 \(\Delta \nu\) の比 \(\nu / \Delta \nu\) で Q を定義する。また、Q 値は、空洞共振器中に貯えられたエネルギーと、空洞共振器内におけるエネルギー損失の比としても表わされる。
空洞共振器内のエネルギー損失は、共振器内の媒質が無損失の場合には、すべて共振器内の壁面上を流れる高周波電流のジュール熱に相当する。このような場合の Q値を無負荷の Q 値とよび、Q0 と記す。
空洞共振器内の常磁性物質が磁気共嗚吸収(マイクロ波のエネルギーを吸収)することにより、共振器の Q 値が変化する。この Q 値の変化を電気信号としてとらえる装置が EPR 装置である。 -
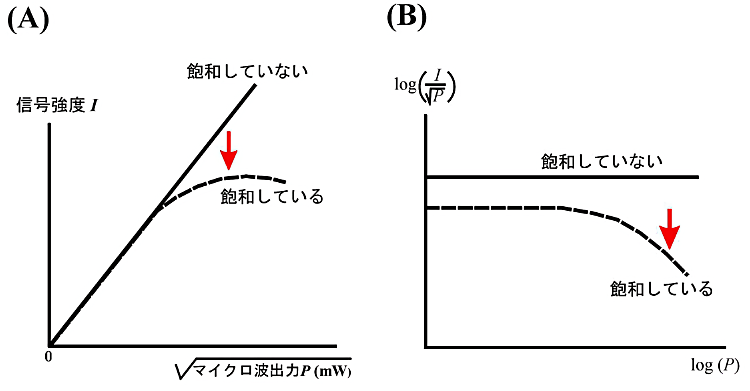
図3:飽和の観測
(A)EPR 信号強度(\(I\))を使用マイクロ波出力(\(P\))の平方根でグラフにした。グラフが比例関係を表している範囲では飽和は観測されていないが、信号強度が比例直線の下方にずれてくると飽和が観測される。
(B)(A)のグラフの傾きとマイクロ波出力の関係を対数でグラフ化した。 -
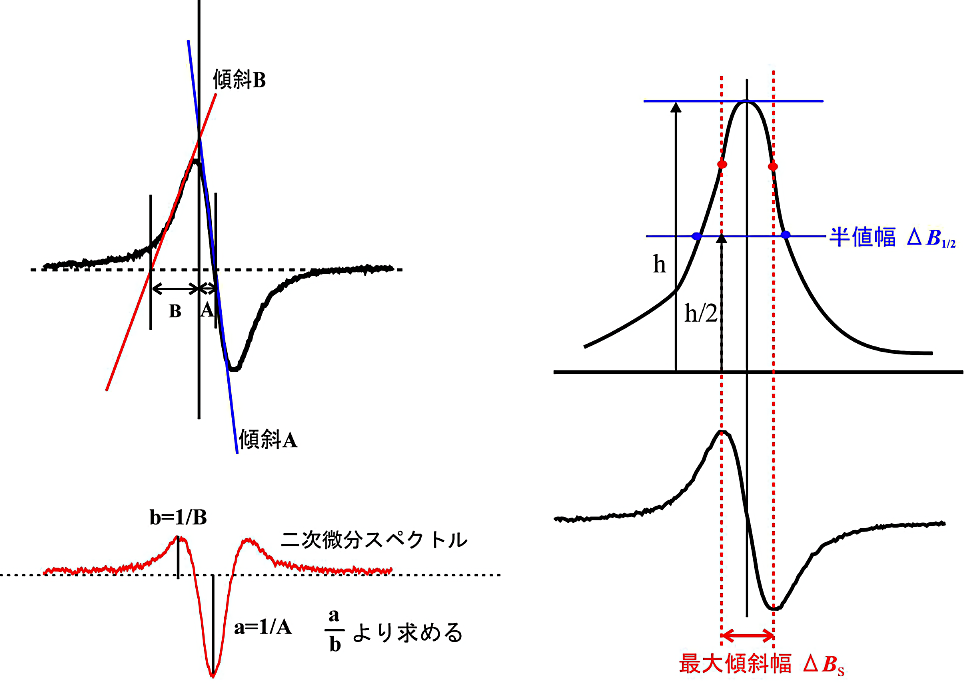
図4:ローレンツ型、ガウス型の見分け方
傾斜法(左図)では、典型的なガウス型は \(\mathrm{B/A} = 2.2\)、ローレンツ型は \(\mathrm{B/A} = 4\) となる。
右図は吸収の半値幅 \(\Delta \boldsymbol{B}_{1/2}\) と微分曲線の最大傾斜幅 \(\Delta \boldsymbol{B}_{\mathrm{S}}\) の比で線形を見分ける方法を示している。ローレンツ型では1.731、ガウス型では1.177となる。 -
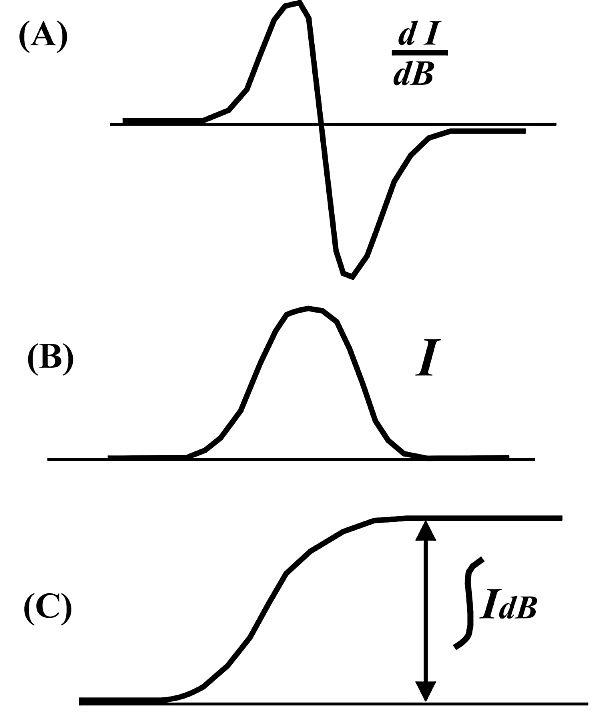
図5:スピン濃度の定量測定
(A)一次微分で記録された EPR スペクトル
(B)(A)を一回積分して求められた EPR 吸収
(C)二回積分で得られた EPR 吸収の面積(矢印部分) -
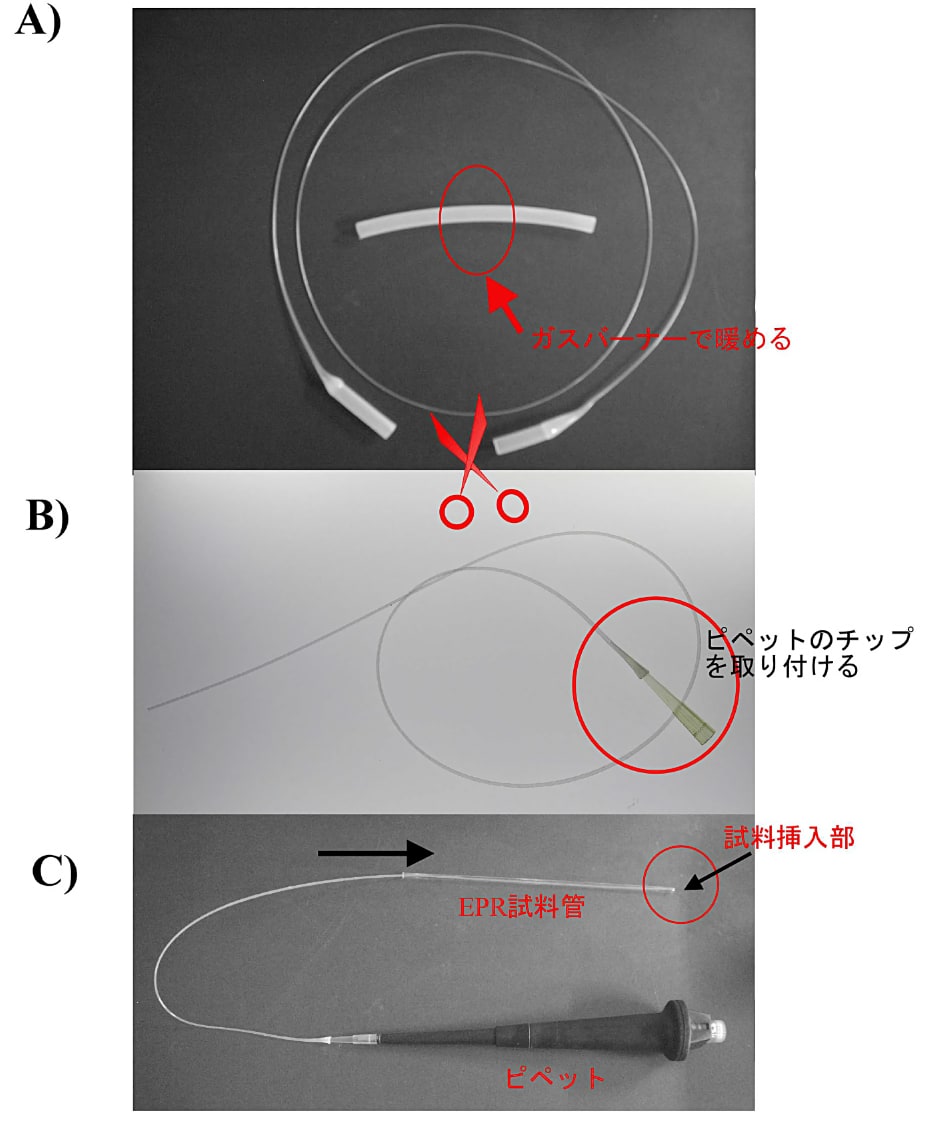
図6:試料を EPR 試料管へ入れる方法
A)外径 8 mm、肉厚 1 mm 程度のポリエチレンチューブ約 10 cm の中央部をガスバーナーで回転させながら暖め(少し膨れて透明になったら)、ゆっくりと 1 m 程度引き伸ばす。
B)引き伸ばしたチューブを半分に切断し、太いパイプ部分を適当な内径になるように切断し、ピペットのチップをしっかりはめ込む。
C)作製した自在型チップをピペットに取り付け、必要量の試料を吸い上げ、EPR 試料管内壁に付着しないように試料管の底部に直接試料を挿入する。 -

図7:嫌気用 EPR 試料管の作り方
A)ネジぶた、B)ネジぶたの内径に合うコルクホーラーで打ち抜いた肉厚 4 mm の飴ゴムセプタム、C)パイレックス製ネジ付き試験管(13 × 100 m/m 例えば、IWAKI の TST-SCR13-100 など)、D)スプラジル石英 EPR 試料管
パイレックス管と石英試料管が段継された(矢印で示す) EPR 試料管を準備する。パイレックス試験管の中央部を切断し、ガスバーナーで熱して段継 EPR 試料管のパイレックス部分と溶接する(赤丸印)。自分でガラス細工が出来ないときは業者に依頼する) -
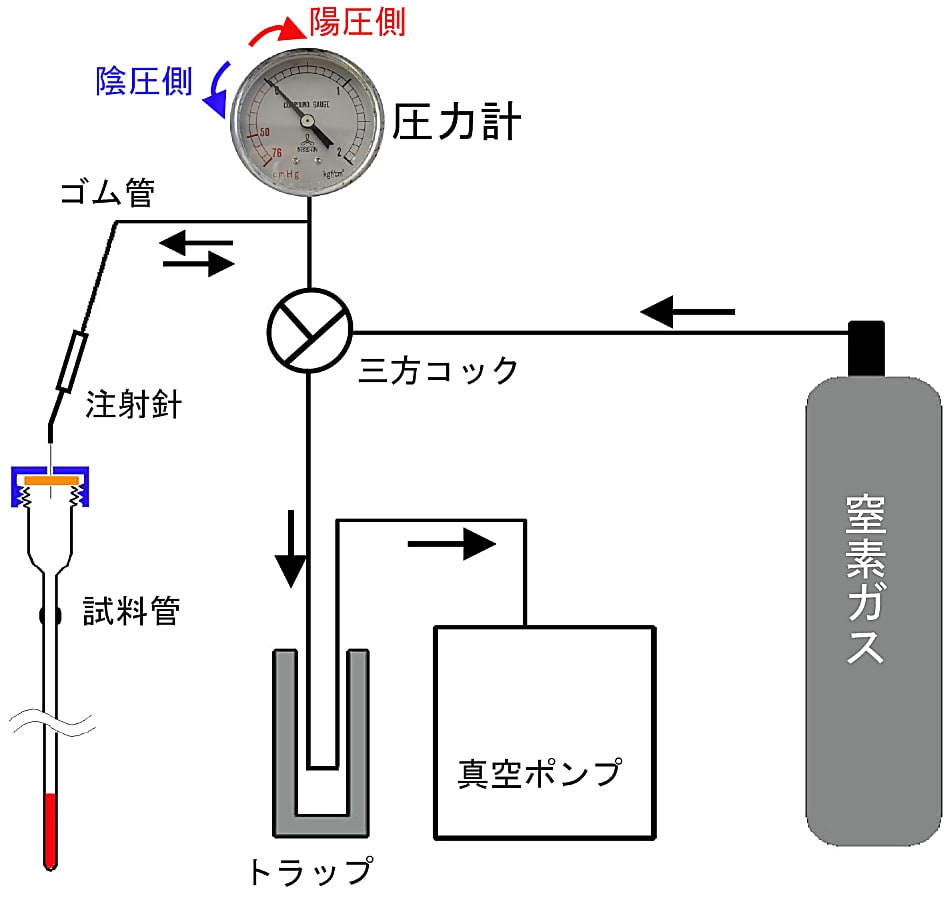
図8:嫌気条件で EPR 試料を調整する方法
真空ラインを用いて試料管内を脱気し、窒素ガスを注入する。この一連の作業を数回繰り返した後、少し加圧目(+0.2 気圧程度)の状態で、ネジキャップ付き試料管(または試験管)のセプタムから注射針を抜きとる。圧カゲージは陰圧側も計測できるタイプを使う(目盛のゼロは1気圧を示す)。黒矢印はガスの移動方向を示す。真空ポンプ保護のため、水分のトラップは不可欠である。 -
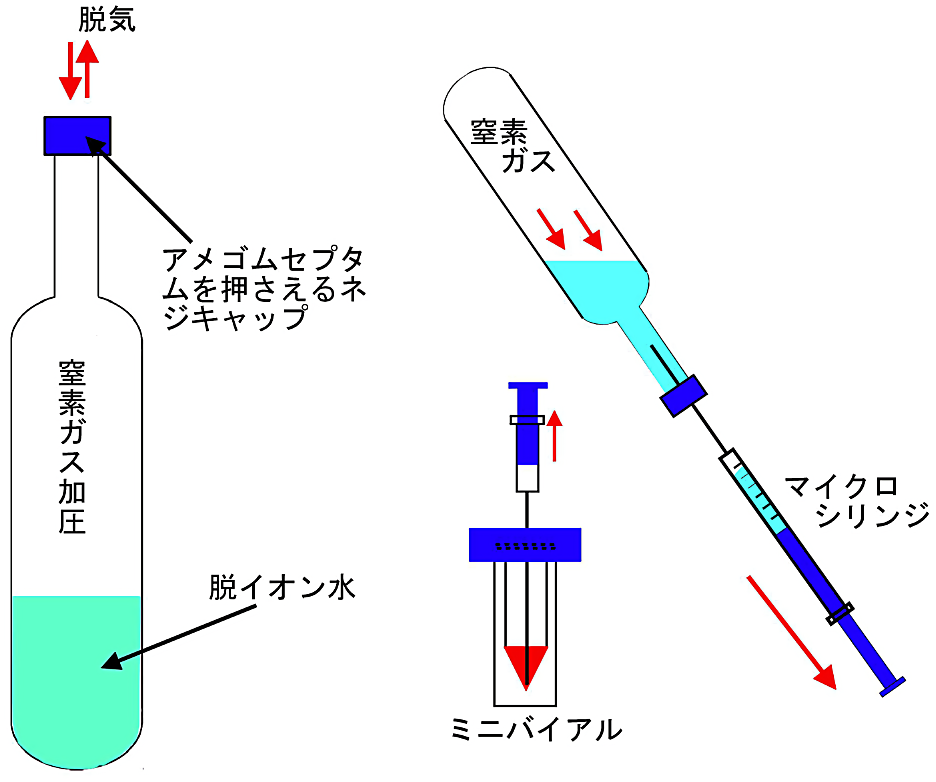
図9:嫌気状態の脱イオン水や試料標品の取り扱い
パイレックスガラスで左図のような脱気用試験管を用意する。簡単に自作できる。細い首の部分は外径 13 mm φ(IWAKI の TST-SCR13-100 など)のネジ付きパイレックス試験管を適当な長さに切断して、外径 40 mm φ 程度のパイレックス試験管と溶接する。太さや長さは使用目的に合わせて決めればよい。(ガラスエ作上の注意としては溶接部分のガラスが薄くなったり、歪が残らないようにガラス工作をすることである。)
嫌気状態の脱イオン水や試料票品を窒素ガスの圧力を使ってマイクロシリンジに移す(右図)。 -
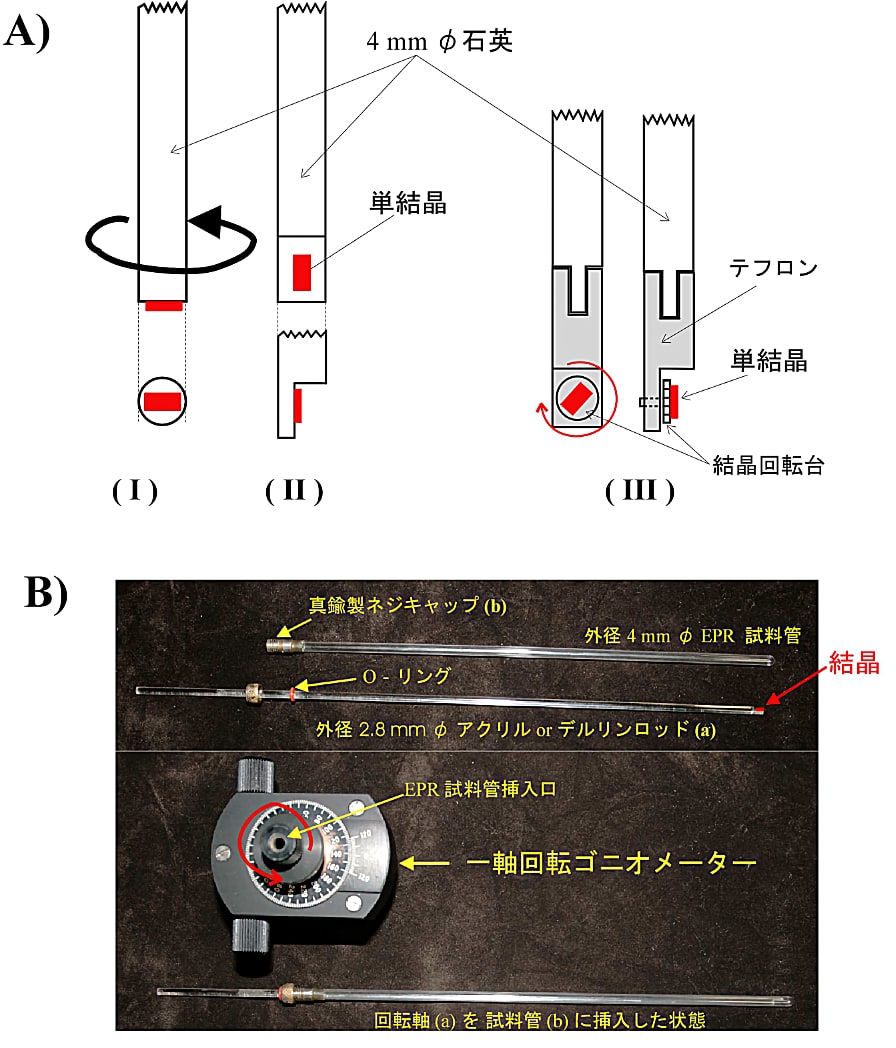
図10:一軸回転用単結晶 EPR ゴニオメーター
(A)(I)、(II)はそれぞれの結晶軸の周りでの回転ができる。(III)はテフロン製回転台を回転させて、任意の軸方向で回転できる。
(B)液体ヘリウムのフロークライオスタットを使う場合:単結晶をアクリルまたはデルリン製の結晶回転用ロッド(a)の先端にマウントし、結晶が落下しないように EPR 試料管の(b)より挿入し、ネジ付キャップ/O-リングで試料管内に封入する。この単結晶用試料管をフロークライオスタット上部に固定したゴニオメーターに固定し、ロッドを1度刻みの精度で回転させる。 -
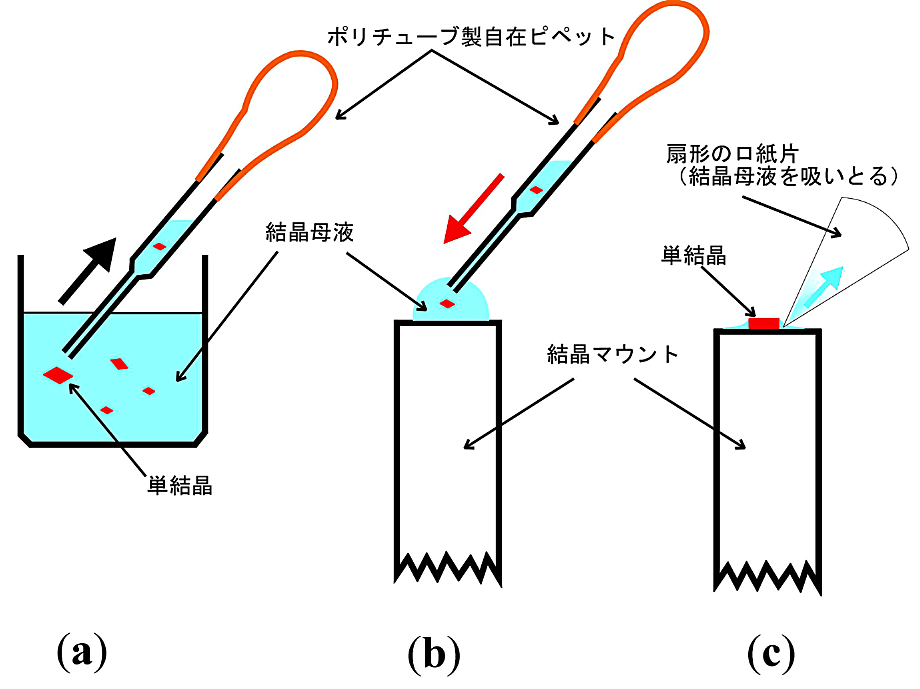
図11:単結晶を結晶回転軸に取り付ける方法
(a)ポリエチレンチューブで作製した自在ピペットで1個の単結晶を母液ごと吸い上げる。
(b)結晶マウントの上に単結晶を母液ごと押し出す。母液の水玉の中に単結晶が浮いた状態になる。
(c)扇形のロ紙片で結晶の回りの母液を吸いとる。 -
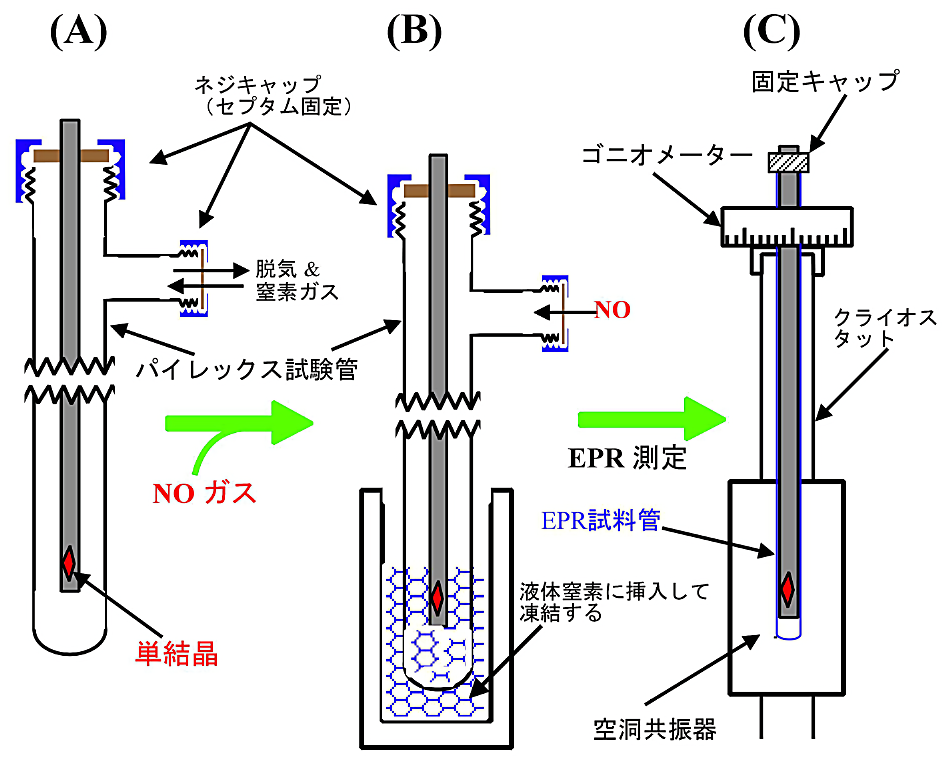
図12:嫌気性の気体配位子分子(例えば、一酸化窒索 \(\ce{NO}\))を還元型ヘムタンパク質のヘム鉄に配位させる方法
還元型ヘムタンパク質の単結晶を結晶回転軸にマウントし、(A)のようなパイレックス試験管内に封入し結晶が乾燥しないように嫌気状態にする。
次に、\(\ce{NO}\) ガスを注入し、氷中で暫く静置した後、パイレックス試験管ごと液体窒素に投入し結晶を凍らせ、同時に結晶を結晶台に固定させる(B)。
結晶回転軸を試験管より素早く取り出し、図10-(B)と同様、EPR 試料管に封入して単結晶 EPR の測定を行う(C)。 -
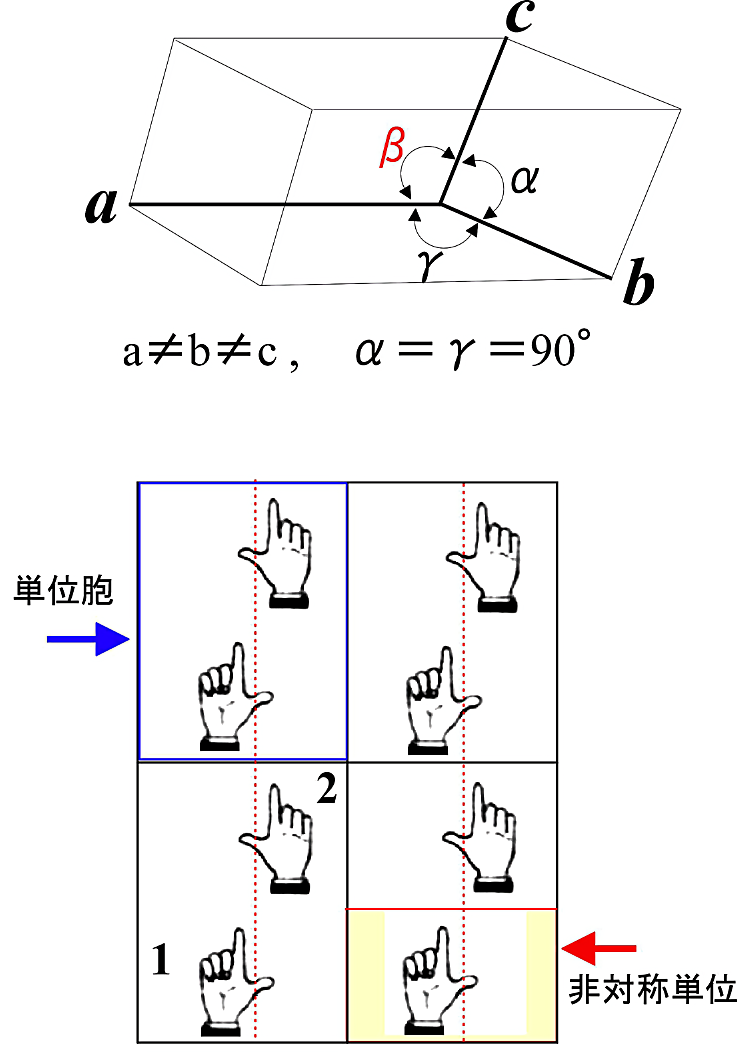
図13:単位格子の形と2回らせん対称
単斜晶系の単位格子の形(上図)
単位胞に2分子(1と2)が存在して \(\boldsymbol{P_{2_{1}}}\) らせん軸(一点鎖線)で関係づけられている場合の結晶構造(下図) -
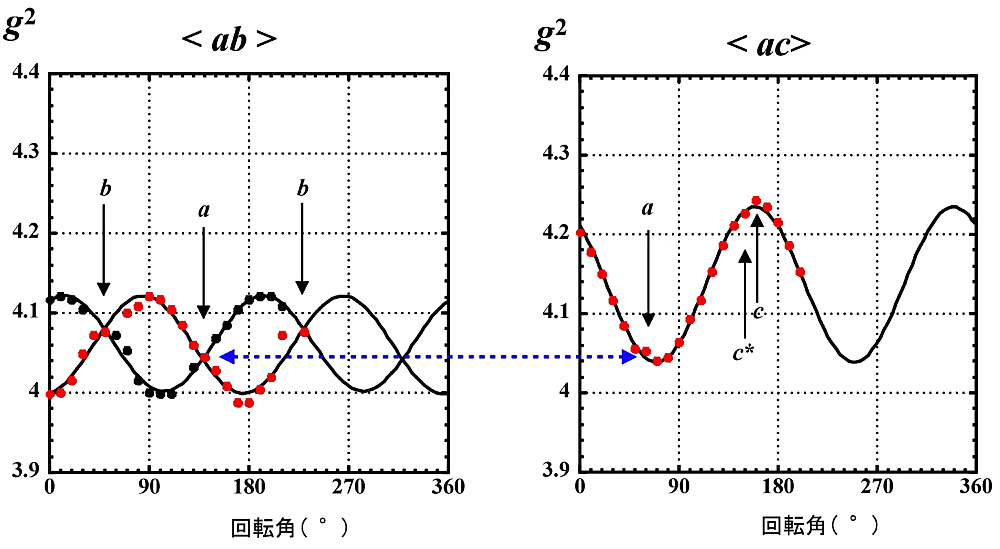
図14:結晶軸回りの \(\boldsymbol{g^{2}}\)–回転角度プロット例
\(\boldsymbol{P_{2_{1}}}\) 空間群をもつタンパク質の単結晶で、左のプロットは \(\boldsymbol{ab}\) 面内で結晶を回転させた時に得られる EPR 信号から\(\boldsymbol{g}\)-値を読み取り、\(\boldsymbol{g^{2}}\) と回転角度の関係をプロットした。結晶軸の前後で曲線は対称になる。
右図は2回らせん軸の回りで回転させた場合で(\(\boldsymbol{ac}\) 面内)、単位胞中の2分子が等価になるので、曲線は1本になる。\(\boldsymbol{ab}\) 面内の測定で得られた \(\boldsymbol{a}\)-軸方向の \(\boldsymbol{g}\)-値(\(\boldsymbol{g_{a}}\))を \(\boldsymbol{ac}\) 面内の曲線上に対応させる(青色鎖線矢印)ことが出来る。 -
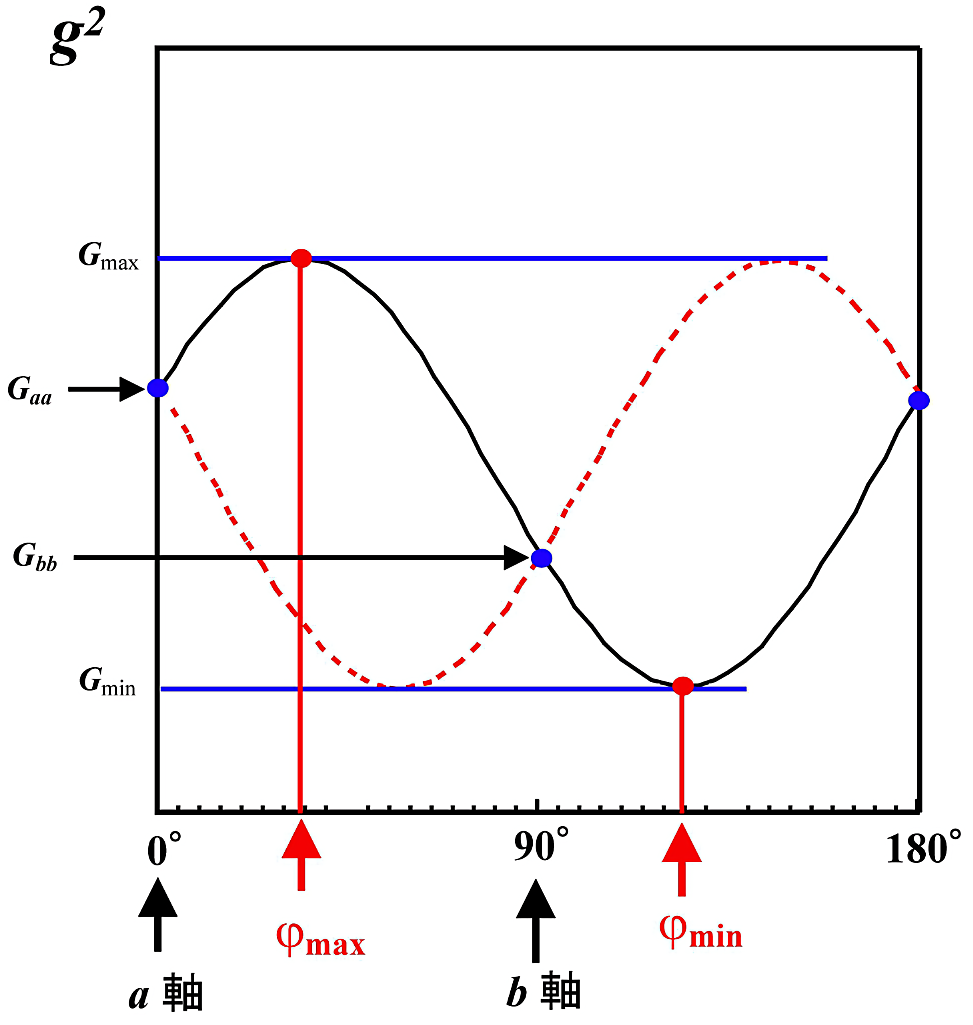
図15:\(\langle \boldsymbol{ab} \rangle\) 面内における \(\boldsymbol{g^{2}}\) の角度変化 -
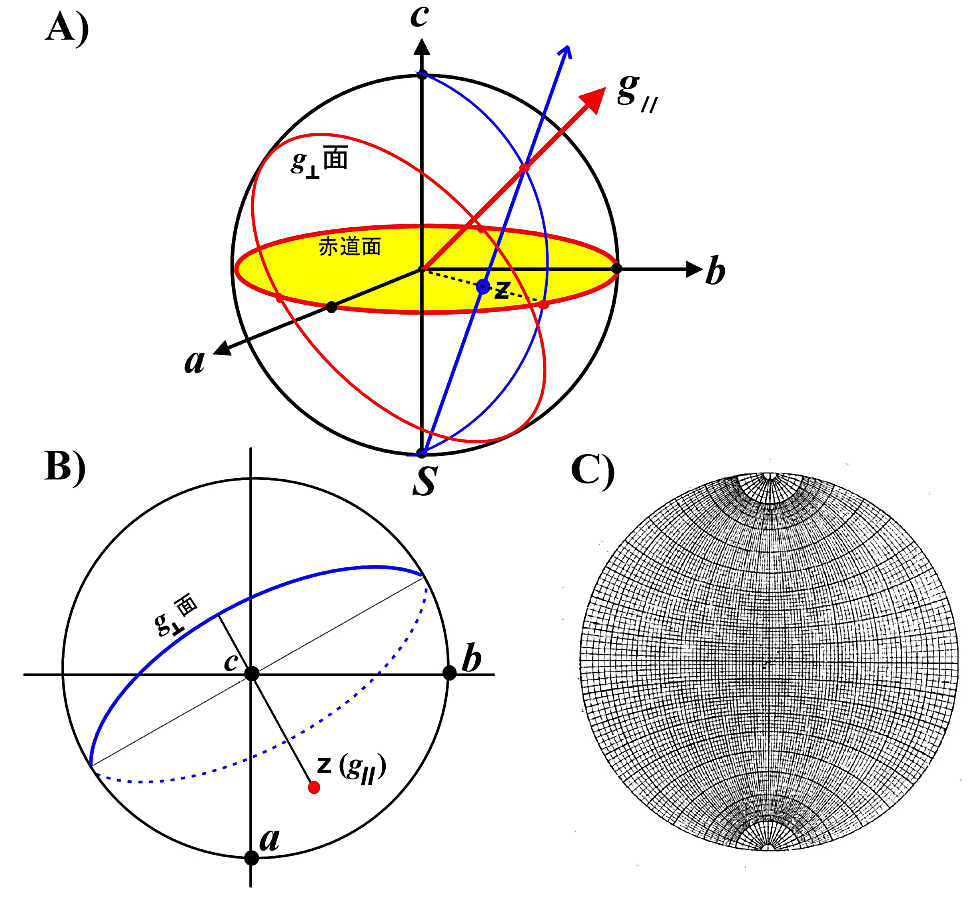
図16:ステレオ投影図による表示
A)3次元空間での \(\boldsymbol{g_{\parallel}}\) ベクトルを2次元平面上の点z として投影する。単位長の半径をもつ球を直交座標 \((a\text{、}b\text{、}c)\) 上に考える。次に、原点より \(\boldsymbol{g_{\parallel}}\) 方向にとった直線(赤矢印線)が球面を切る点とこの球の南極(\(\boldsymbol{S}\))とを結ぶ。この直線が赤道面(\(\boldsymbol{ab}\) 面)を切る点を \(\boldsymbol{\mathrm{z}}\) とする。これがステレオ投影法の原理である。
B)例として、結晶 \(\boldsymbol{a}\)、\(\boldsymbol{b}\)、\(\boldsymbol{c}\)-軸、\(\boldsymbol{g_{\parallel}}\)(\(\boldsymbol{\mathrm{z}}\)-主軸)の方向および \(\boldsymbol{g_{\perp}}\) 面(青色実線円弧は赤道面より上、即ち北半球にある事を示しており、青破線円弧は赤道面の下、即ち南半球にある事を示している)をステレオ投影図で示した。
C)あるベクトル \(\boldsymbol{\mathrm{z}}\) の直交座標軸 \((\boldsymbol{a}\text{、}\boldsymbol{b}\text{、}\boldsymbol{c})\) に対する方向余弦が与えられると(\(\boldsymbol{a}\)、\(\boldsymbol{b}\) 、\(\boldsymbol{c}\)-軸からの面角)、図のようなステレオグラフ用紙(ウルフネット)を使って、赤道面上に投影点を決めることができる。ステレオ投影面上の2点(2つのベクトル)間のなす角度はこのウルフネットをステレオ投影面に重ね、回転させて2点間の円弧から読み取る。 -
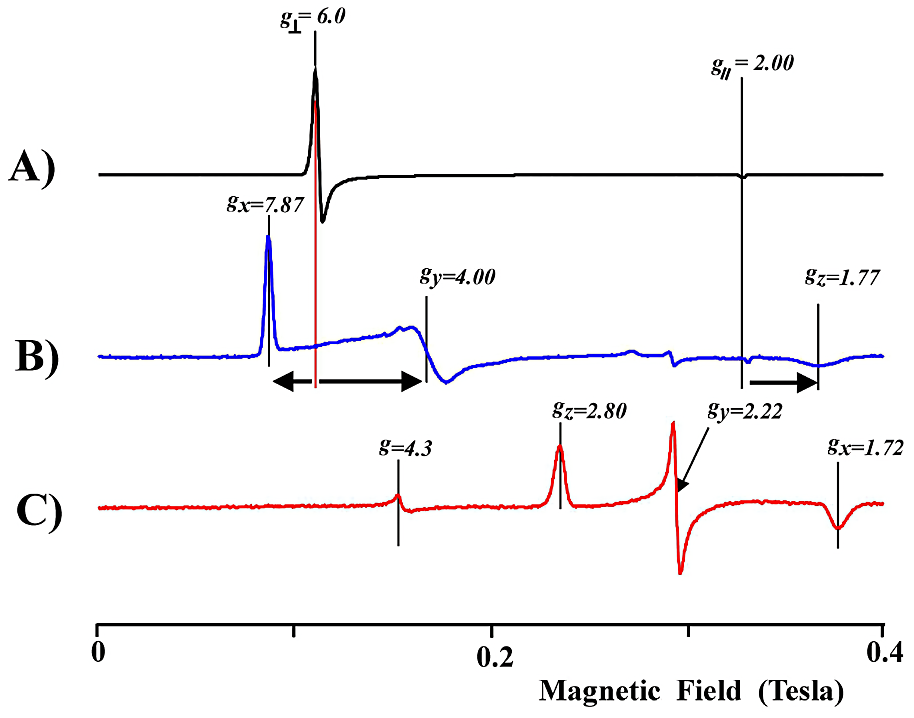
図17:典型的な酸化型ヘムタンパク質の EPR スペクトル
A)高スピン型(\(S = 5/2\))ヘムタンパク質:ヘム面が軸対称な場合例としてアコメト Mb を示す。
B)高スピン型(\(S = 5/2\))ヘムタンパク質:ヘム面内に異方性がある場合例として基質カンファー結合型 P450cam を示す。\(g6\) を中心に \(g_{\mathrm{x}}\)、\(g_{\mathrm{y}}\) の分裂がみられる。\(g_{\mathrm{z}}\) の信号は \(g2\) より高磁場側にシフトする。
C)低スピン型(\(S = 1/2\))ヘムタンパク質:\(g2\) を中心に \(g_{\mathrm{z}} > g_{\mathrm{y}} > g_{\mathrm{x}}\) の順に \(g\) 値の異方性がみられる。アザイド結合型 Mb(\(\ce{MbN3}\))の例を示した。
測定温度:スペクトル A)と B)は 5 K 、スペクトル C)は 15 K のデータである。 -
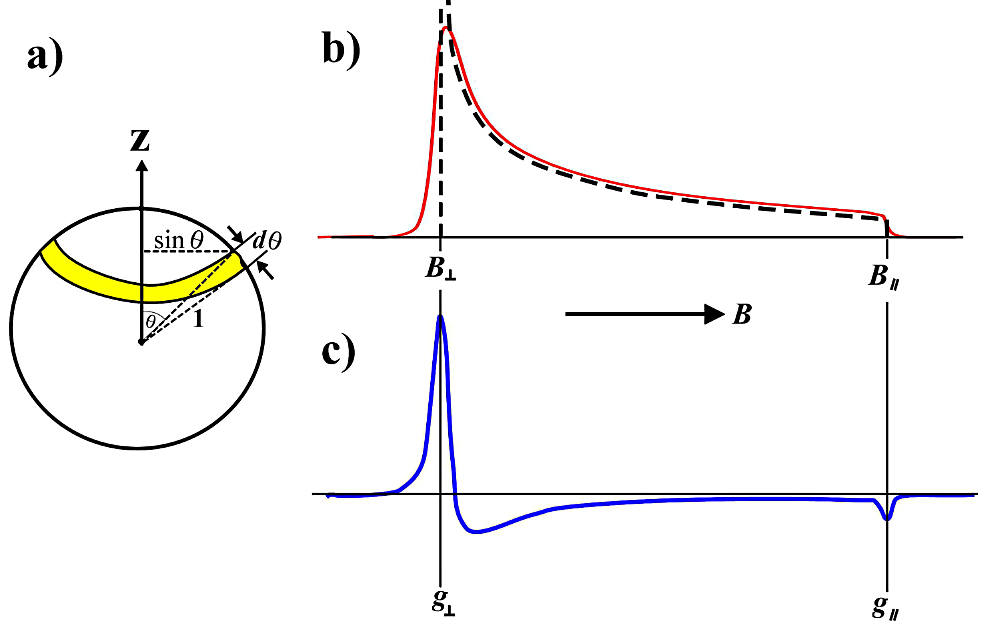
図18:軸対称(\(\boldsymbol{g_{\perp}} > \boldsymbol{g_{\parallel}}\))な \(\boldsymbol{g}\) 因子による無秩序配向 EPR スペクトルの線形
a)磁場の向きの確率を表す単位球。常磁性分子種が無配向で、あらゆる配置をとって空間分布しているとき、分子に固定した主軸座標からみると同じ確率で磁場があらゆる方向を向くことになる。磁場の向きが \(\theta\) から \(\theta + \mathrm{d} \theta\) の間にある確率は図の黄色帯状の面積に比例する。この確率は \(\theta\) に対応する共鳴磁場を生じる確率になる。
b)これより空間平均をとったスペクトル強度(線形関数)が得られる。この線形関数には分母に \((B^{2} - {B_{\perp}}^{2})\) の項が含まれるので、スペクトルに線幅がないとすると、吸収強度は \(\boldsymbol{B_{\perp}}\) で無限大になり、\(\boldsymbol{B_{\parallel}}\) で勾配が不連続になる(破線の曲線)。実際の吸収線は、ある線形と線幅を持っているので、無秩序配向の線形は赤色で示した実線のようになる。
C)実際に測定される一次微分曲線を青色実線で示す。二つのピークから \(\boldsymbol{B_{\perp}}\) と \(\boldsymbol{B_{\parallel}}\) を求めることができる。したがって、\(\boldsymbol{g_{\perp}}\) と \(\boldsymbol{g_{\parallel}}\) が決定される。 -
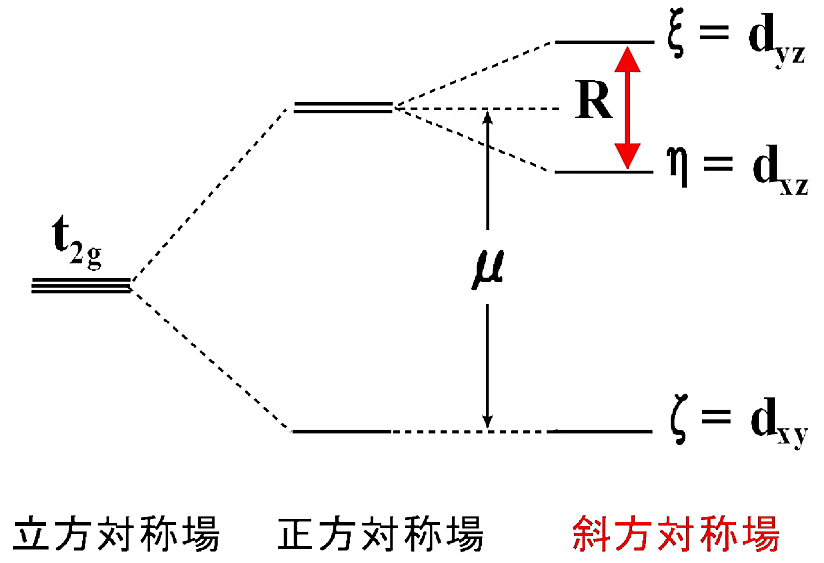
図19:\(\boldsymbol{t_{2_{g}}}\) 軌道のエネルギー準位
\(\boldsymbol{\mu}\) は軸対称の歪(正方対称場)、\(\boldsymbol{R}\) は斜方向の歪(斜方対称場)を表す。1空孔による計算では、エネルギー準位が逆転する。 -
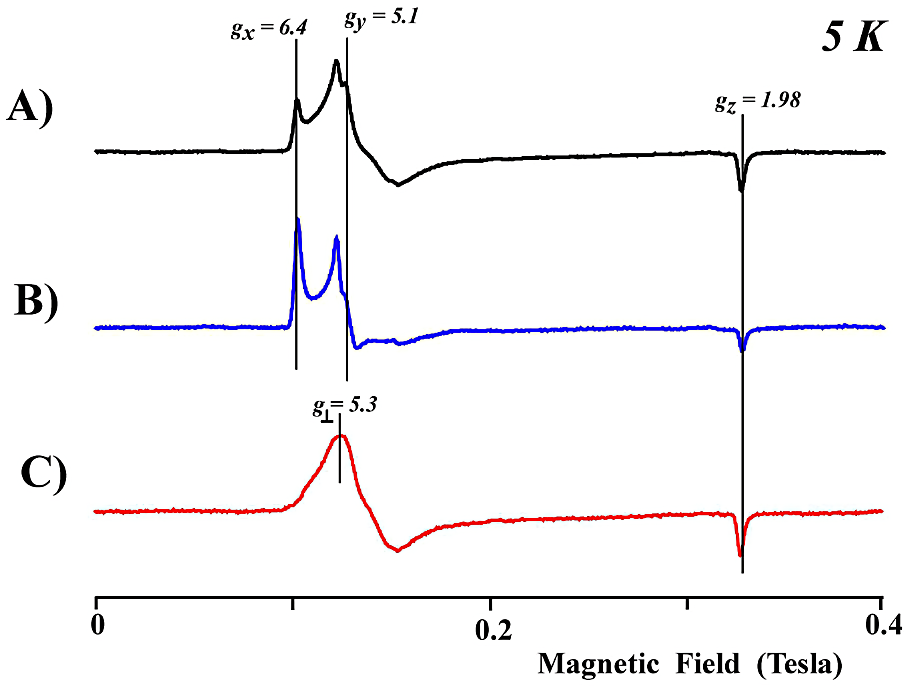
図20:西洋ワサビペルオキシダーゼ(HRP)の EPR スペクトル
A)リン酸緩衝液(KPB, pH 7.0)での EPR スペクトル。\(g_{\mathrm{x}} = 6.4\)、\(g_{\mathrm{y}} = 5.1\) 以外にブロードな吸収がみられる。
B)HEPES 緩衝液(pH 7.0)での EPR スペクトル。ブロードな吸収を示す成分が少なくなっている事が分かる。
C)スペクトル A)からスペクトル B)にある係数を掛けて差をとり、ブロードな吸収を示す成分だけの EPR スペクトルを分離した。
測定温度は 5 K である。スペクトル解析には GRAMS/AI 8 を用いた。 -
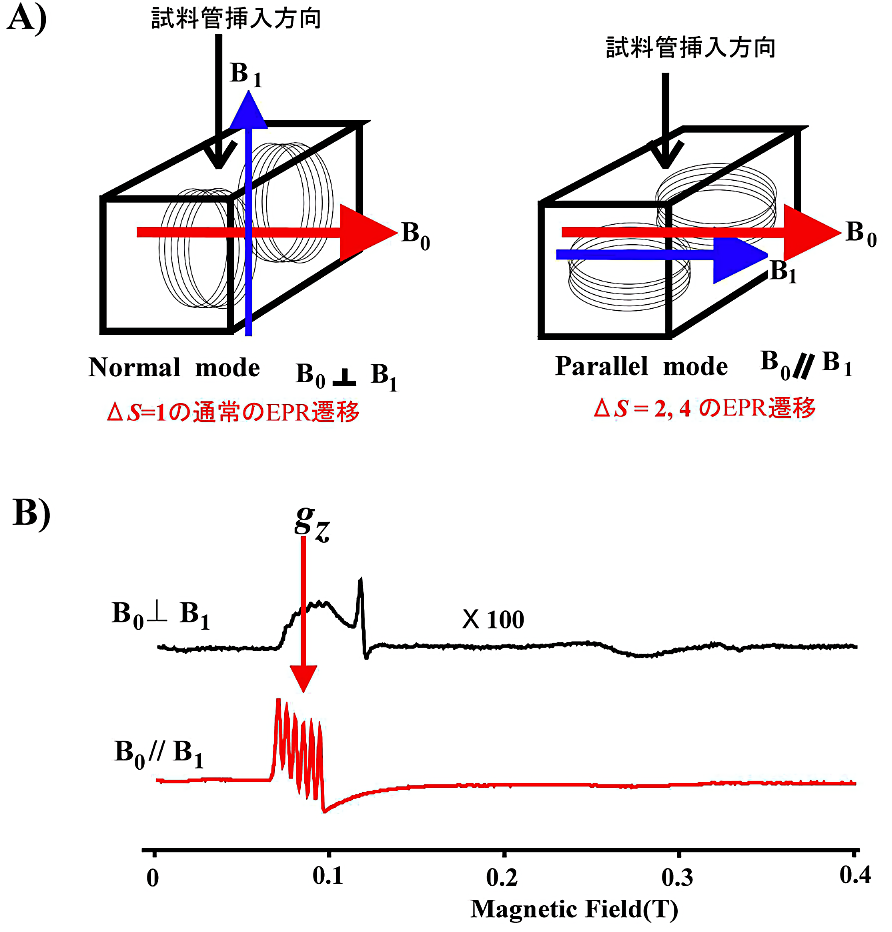
図21:二重モード矩形 TE1O2 空洞共振器と \(\boldsymbol{\ce{Mn^{3+}Mb}}\) の EPR スペクトル
A)二重モード空洞共振器の慨形。\(B_{0}\) は外部磁場、\(B_{1}\) はマイクロ波磁界を示す。
B)\(\ce{Mn^{3+}Mb}\)(\(S = 2\))の測定例。\(\Delta S = 2\) の遷移を parallel mode(\(B_{1} \parallel B_{0}\))で観測すると、信号強度が normal mode(\(B_{0} \perp B_{1}\))の約100倍になっている。測定温度は 5 K である。 -
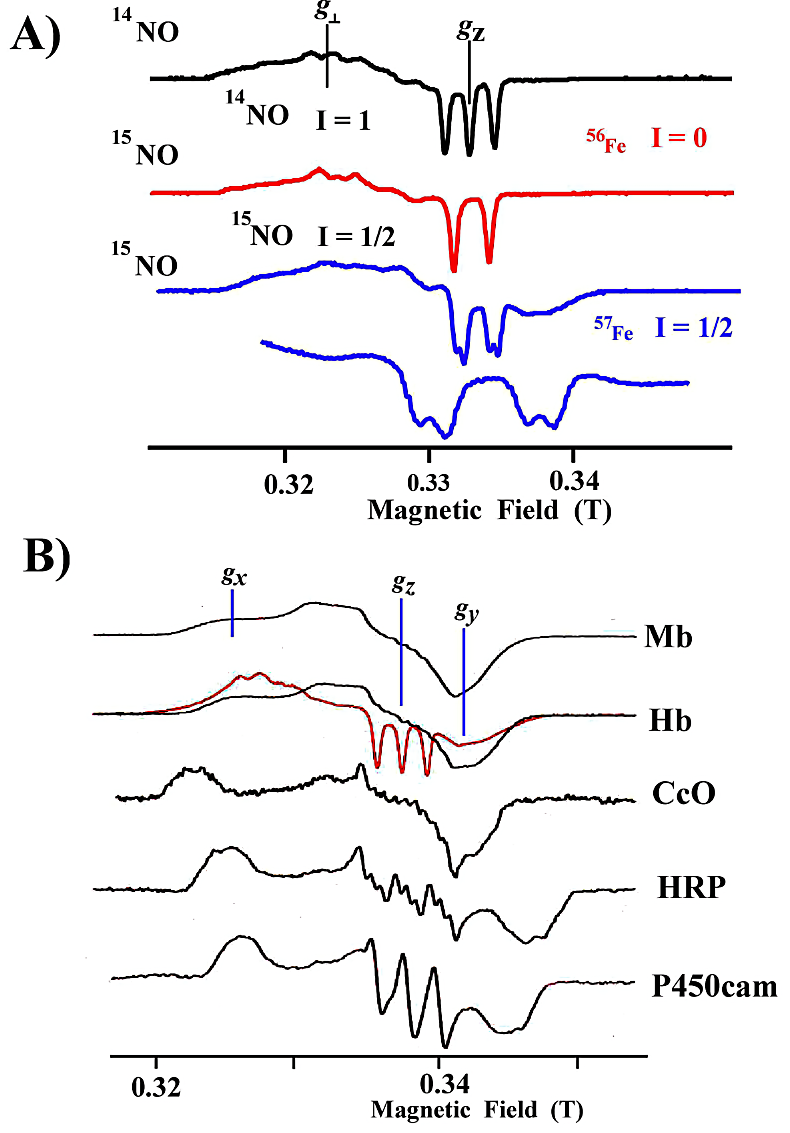
図22:\(\ce{NO}\) 結合型ヘムタンパク質の EPR スペクトル(77 K)
A)5配位型 \(\ce{NOHb}\) の EPR スペクトル。\(\ce{^{14}NO ^{56}Fe}\)、\(\ce{^{15}NO ^{56}Fe}\)、\(\ce{^{15}NO ^{57}Fe}\) の hfs 分裂の様子を示す。
B)6配位型 \(\ce{NO}\) ヘムタンパク質の EPR スペクトルを示す。Mb、Hb(赤線スペクトルは5配位構造)、CcO、HRP、P450cam -
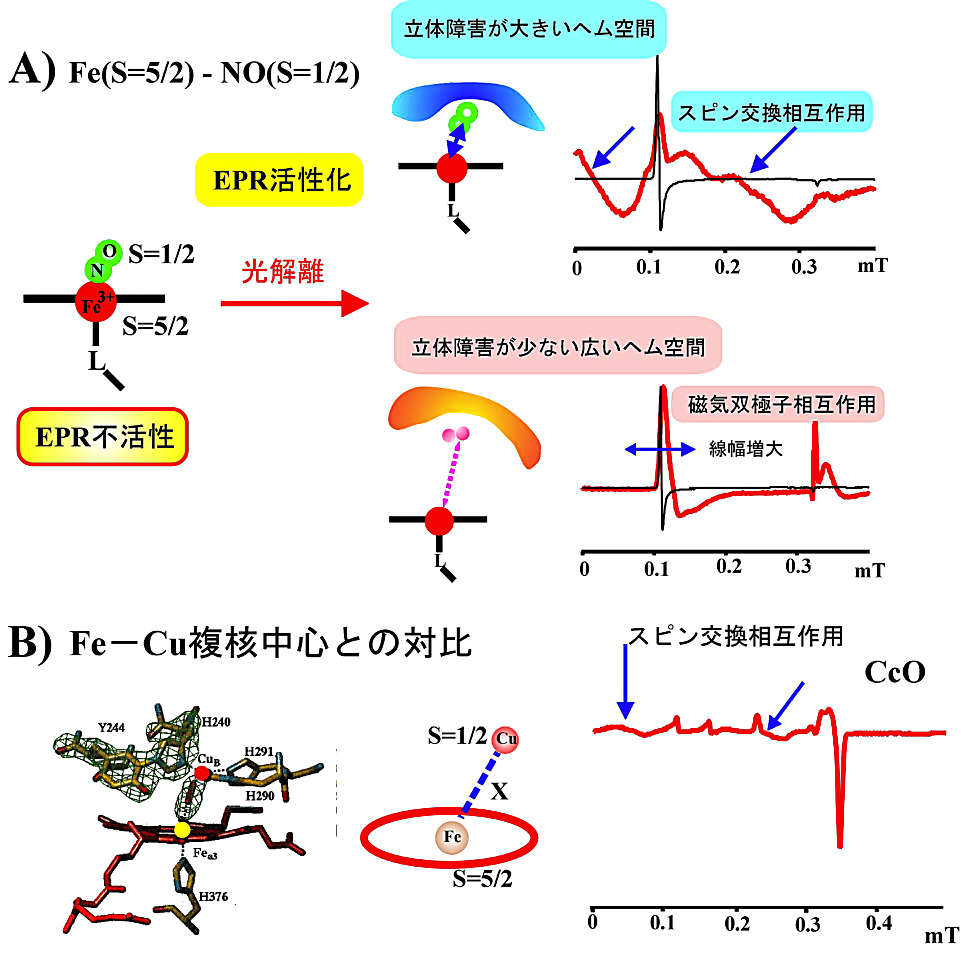
図23:酸化型 Mb-\(\ce{NO}\) の光照射で現れる特異な EPR スペクトル
A)EPR 不活性な酸化型 Mb-\(\ce{NO}\) を低温で光照射すると、光解離した \(\ce{NO}\) が遠位ヘムポケット内でトラップされる様子を示す。遠位残基による立体障害があるときは \(\ce{NO}\)(\(S = 1/2\))とヘム鉄(\(S = 5/2\))の間でスピン交換相互作用が働き、零磁場近傍にブロードな吸収が現れる(上図)。立体障害が小さいと解離 \(\ce{NO}\) はヘム鉄から遠のきヘム鉄の \(g6\) 信号は磁気双極子相互作用で線幅増大を示す(下図)。
B)酸化型 c シトクロム酸化酵素(CcO)の活性部位の構造と高スピンヘム鉄(\(S = S/2\))と \(\ce{Cu}\)(\(S = 1/2\))のスピン交換相互作用にも同様な EPR スペクトルがみられる。 -
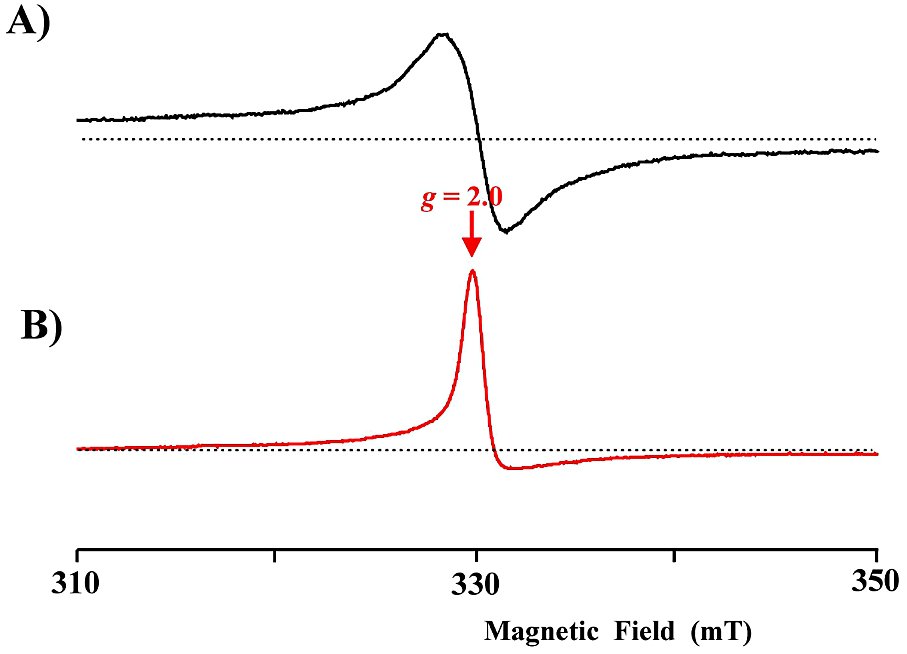
図24:西洋ワサビペルオキシダーゼ(HRP)と過酸化水素の反応
A)リン酸緩衝液(pH 7.0)での HRP Compound I の EPR スペクトル
B)HEPES 緩衝液(pH 7.0)での HRP Compound I の EPR スペクトル
点線はベースラインを示す。A)は線幅の広い信号であることが分かる。測定温度はいずれも 5 K である。 -
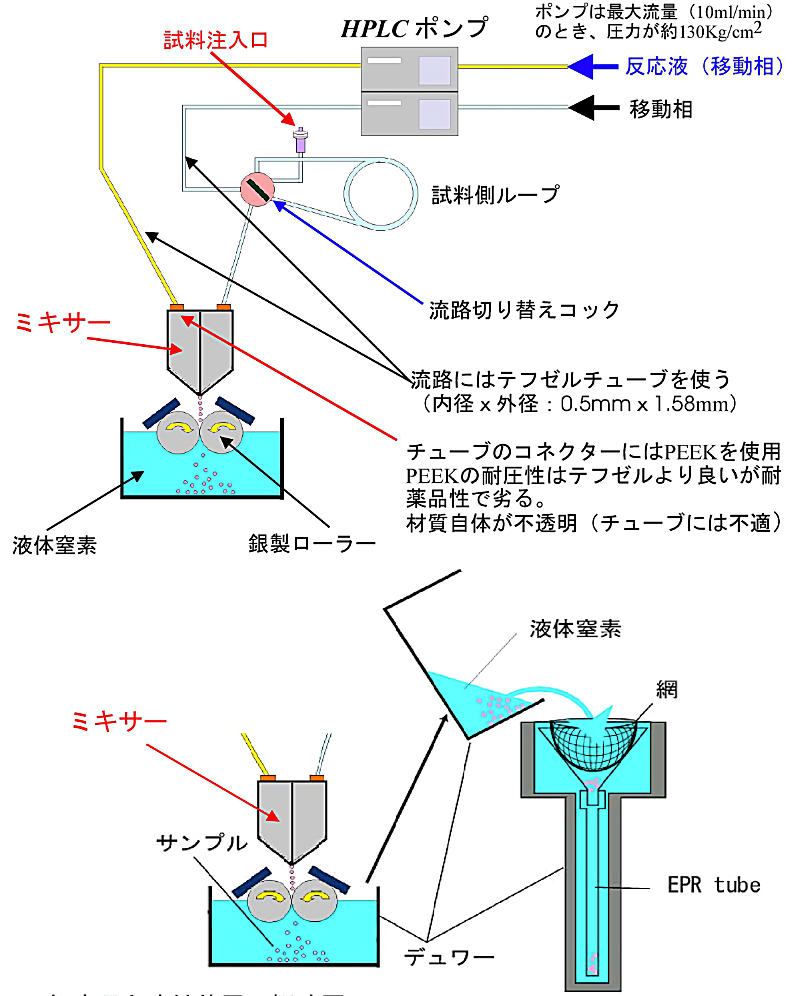
図25:急速混合凍結装置の概略図
急速混合装置の概略図(上図)と EPR 試料管に凍結試料を移す方法を示す(下図)。図のような、上部の口径が大きい特殊なデュワー瓶の中に EPR 試料管とロート、ステンレス製網を入れる。凍結試料を一気にこのデュワーに注ぎ入れる。大きな試料は網で除去される


