概要
蛋白質のリガンド結合反応やコンフォメーション変化は,蛋白質が機能するための重要なプロセスである。多くの場合,これらの実測には吸光測定や蛍光測定が用いられる。実測されたデータから平衡定数等のパラメータを算出するためには,最小自乗フィッティングによる解析が用いられる。吸光測定・蛍光測定の原理や化学熱力学・平衡論については講義や実験のチュートリアル等で話を聴く機会も多い。しかし,測定データと平衡論を組み合わせて数学的に展開するデータ解析手法の原理については,まとまった解説を聴く機会は少ないかもしれないし,あるいは解析は全てコンピュータ任せという人も多いかもしれない。しかし,複雑な結合様式やコンフォメーション変化を測定データの中から見いだすためには,データ解析の原理の理解が不可欠である。そこで,本稿では,解析原理,特に測定データ解析のためのモデル関数をどのように導出するかに重点を置いて解説する。具体的には,蛋白質における1種リガンドの結合平衡反応の吸光測定や蛍光測定データを解析するための原理,そして解析のためのモデル関数の導出の仕方について解説し,さらに解析時の注意点についても指摘する。
1. はじめに
蛋白質が機能し,動作するときには,他の分子との結合やコンフォメーション変化が伴う。このため,蛋白質の機能を実験的に評価するには,その反応を同定して平衡定数等のパラメータを決定することが実験の現場で必要になることが多い。また,蛋白質の挙動をモデル化して理解したり予測したりするには,平衡論で反応スキームを描くことがしばしば必要である。しかし,記号と矢印で反応スキームを描くのは出発点に過ぎない。実験データと照らし合わしてその反応スキームの妥当性を検討し,さらには解析を行って平衡定数等の算出をすることで,議論や応用の対象になるのである。そのような解析においては,反応スキームがどのように実験的に測定されるかを記述するモデル関数を導出することが重要なステップである。
吸光測定や蛍光測定は,蛋白質のリガンド結合やコンフォメーション変化の平衡反応の測定によく使われる方法である。これは,トリプトファン,補欠分子族,そして蛋白質に結合させた色素の吸光や蛍光の特性が,蛋白質のコンフォメーションやリガンド結合を反映するためである。また,近年,様々な標的分子を検出する蛍光蛋白質センサープローブも開発され,試験管内や生体内の実験で広く使われている[1]。このように測定手法が多様化することで,様々な分子が測定対象となった。そこで,以下では,測定された吸光度や蛍光強度データを適切に取り扱うための解析の基本原理について述べる。蛋白質の平衡反応の測定データはしばしば最小自乗フィッティングで解析され,リガンドの結合定数やコンフォメーション間の平衡定数といった解析値が算出される。最小自乗フィッティングによる解析の要となるのは,解析のためのモデル関数を導出することである。実験データを解析するための多くのモデル関数には,
- リガンド濃度等の独立変数に対する,各蛋白質分子種のモル分率の応答を与える項
- 各蛋白質分子種のモル分率を関数とする,測定強度の理論値を与える項
が含まれる[2]。研究室によっては,そのようなモデル関数をどのように立てるのかといった基本原理について指導を行っているところもあるかもしれないし,あるいはあまりに明らか過ぎるために具体的な解説や指導もなく,先輩の院生やスタッフから言われるままに解析手順を学生が踏襲しているところもあるだろう。筆者自身は逆の立場で,これまでに学生に吸光や蛍光測定データを使った蛋白質平衡反応解析の方法を指導する機会が時々あった。そのような指導を繰り返すうちに,指導内容に加えてそれに関連する内容を合わせてまとめておきたいと思い立った次第である。そこで,本稿では,蛋白質の平衡反応の吸光度データや蛍光強度データを解析するための基本原理をあえて確認し,さらにいくつかの例題を示しながら解析の方法について解説することにした。
2. データ解析に用いるモデル関数を導出するための基礎事項
本稿を通して,測定下の蛋白質 \(\mathrm{M}\) が,
\[ \ce{M_{0} <=> M_{1} <=> \dotsm <=> M_{\mathit{N}}} \tag{2.1} \]
といういくつかのコンフォメーションや化学状態の平衡にあるときに,測定される吸光度あるいは蛍光強度(以降,両者を区別しないときは単に「強度」と総称することにする)を記述するモデル関数を立てることを目標とする。この平衡反応は,コンフォメーション間の平衡と考えても良いし,あるいはリガンドの結合と考えても良く,本稿ではいずれも取り上げる。反応 (2.1) を吸光測定や蛍光測定で解析する過程で本稿が使う基礎事項は以下の2つである。
2.1. 測定強度の線形性(斉次性と加法性)
反応 (2.1) の平衡状態にある蛋白質を吸光測定や蛍光測定で解析することを想定する。蛋白質のある分子種 \(\ce{M_{\mathit{k}}} \ (k = 0, 1, \dots , N)\) のモル分率が 100% の時の強度を \(A_{k}\) としたとき,平衡状態において測定される強度 \(A\) のモデル関数を
\[ A_{\textrm{model}} = \alpha_{0}A_{0} + \alpha_{1}A_{1} \dots + \alpha_{N}A_{N} \tag{2.2} \]
という線形結合で記述する[2]。ここで,\(\alpha_{k}\) は,測定下の蛋白質分子種 \(\textrm{M}_{k}\) のモル分率
\[ \alpha_{k} = \frac{[\mathrm{M}_{k}]}{\displaystyle \sum^{N}_{k = 0}[\mathrm{M}_{k}]} \tag{2.3} \]
である。式 (2.2) では,測定強度値における \(\mathrm{M}_{k}\) の寄与分が \(\alpha_{k} \cdot A_{k}\) であること(すなわち,強度は \(\mathrm{M}_{k}\) の濃度に比例すること,つまり斉次性),そして \(\mathrm{M}_{0}, \mathrm{M}_{1} \dots\) の強度寄与分の加法性が成り立つことを前提としている。
測定強度のモデル関数において式 (2.2) のような線形結合を許す根拠は何か?吸光度については,その発色団濃度に対する比例を示した Beer–Lambert の法則[3]である。また,蛍光強度については名前の付いた法則はないが,測定対象に含まれる蛍光源である発色団の濃度が増えると,それに比例して検出器に到達する蛍光由来の光子数は増加すると考えられる。さらに,吸光測定や蛍光測定に限らず,以上のような線形性を適用できる測定データ対しては,式 (2.2) の形のモデル関数を使うことが可能である。ただし,上記の法則が前提となるため,線形性が適用できる条件(十分希薄な濃度であるか等)において実験することも心がけなければならない。
2.2. 質量作用の法則
質量作用の法則(mass action law)は,
\[ \ce{\mathit{p}_{1}A_{1} + \mathit{p}_{2}A_{2} + \dotsm <=> \mathit{q}_{1}B_{1} + \mathit{q}_{2}B_{2} + \dotsm} \tag{2.4} \]
という平衡反応における反応商(reaction quotient)
\[ K_{\mathrm{eq}} = \frac{[\mathrm{B}_{1}]^{q1}[\mathrm{B}_{2}]^{q2} \dots}{[\mathrm{A}_{1}]^{p1}[\mathrm{A}_{2}]^{p2} \dots} \tag{2.5} \]
の \(K_{\mathrm{eq}}\) が一定であるとするものである。ここでの \(K_{\mathrm{eq}}\) を平衡定数という。\(K_{\mathrm{eq}}\) は反応に含まれる分子種の濃度に依存しないが,温度に依存する。なお,本稿では,活量係数については平衡定数の中に繰り込まれていると考えることで,明示的に取り扱わないことにする。
3. 1個のリガンド結合部位をもつ蛋白質の解析
蛋白質 \(\ce{M}\) とリガンド \(\ce{X}\) の結合反応
\[ \ce{M + X <=>[$K$] MX} \tag{3.1} \]
の吸光あるいは蛍光スペクトルデータの解析を行うことにする。本節では簡単のために,リガンドの結合部位が1個ということを既知とする。本稿で取り扱う解析手順は以下の通りである:
- \(\ce{X}\) の濃度の関数として測定強度を測定する滴定実験を行う。\(\ce{X}\) の濃度変化によって蛋白質分子種 \(\ce{M}\), \(\ce{MX}\) の濃度が変化するので,それに伴って測定強度が変化する。
- 最小自乗法でモデル関数を測定強度データにフィットさせて,結合定数K 等のパラメータを算出する。モデル関数は,\(\ce{M}\), \(\ce{MX}\) の濃度またはモル分率を含む形となる。
通常の実験では,吸光分光光度計や蛍光分光光度計で測定される測定強度の誤差が示す分布は概ね正規分布に近い。したがって,反応に関わるパラメータ値を推定するための回帰分析手法としては,モデル関数と測定値との差分の自乗和の最小化によって最尤推定を行う最小自乗法が相応しい。
3.1. 1波長測定による解析
3.1.1. 解析のためのモデル関数
本節では,反応 (3.1) において測定される測定強度のモデル関数を導出する。反応 (3.1) における平衡定数は,質量作用の法則より
\[ K = \frac{[\mathrm{MX}]}{[\mathrm{M}][\mathrm{X}]} = \frac{[\mathrm{MX}]}{[\mathrm{M}]x} \tag{3.2} \]
である。ここで,\(x\) は遊離しているリガンドの濃度である。式 (3.2) の平衡定数 \(K\) は,(反応式 (3.1) を,リガンド結合する方向にとっていることより)特に結合定数と呼ばれるものであり,(リガンド結合部位が1個の場合の)次元は濃度の逆数である。リガンド結合部位が1個の場合は濃度と同じ次元をもつ解離定数(\(= 1/K\))もよく使われるが,結合部位が2個以上の場合や,2種類以上のリガンドを含む系では,結合定数を用いた方が式中に現れる分数の個数を少なくできるという数式展開の点で都合が良い。結合定数 (3.2) を用いれば,\(\mathrm{M}\), \(\mathrm{MX}\) のモル分率 \(\alpha_{\mathrm{M}}\), \(\alpha_{\mathrm{MX}}\) は,
\[ \alpha_{\mathrm{M}} = \frac{[\mathrm{M}]}{[\mathrm{M}] + [\mathrm{MX}]} = \frac{1}{1 + K_{x}} \tag{3.3} \]
\[ \alpha_{\mathrm{MX}} = \frac{[\mathrm{MX}]}{[\mathrm{M}] + [\mathrm{MX}]} = \frac{1}{1 + K_{x}} \tag{3.4} \]
となる。分子種 \(\mathrm{M}\), \(\mathrm{MX}\) のモル分率が 100% の時の強度をそれぞれ \(A_{\mathrm{M}}\), \(A_{\mathrm{MX}}\) として式 (3.3),(3.4) を式 (2.2) に適用すれば,
\[ A(x) = \alpha_{\mathrm{M}}A_{\mathrm{M}} + \alpha_{\mathrm{MX}}A_{\mathrm{MX}} = \frac{1}{1 + Kx} A_{\mathrm{M}} + \frac{Kx}{1 + Kx} A_{\mathrm{MX}} \tag{3.5} \]
が得られる。これが,反応 (3.1) の測定強度についてのモデル関数である。
図1に式 (3.5) のモデル関数を適用した解析例を示す。図1Aのスペクトルの波長 \(\lambda_{1}\) から吸光度をとり,リガンド濃度に対してプロットしたのが図1Bである。このプロットに対して,式 (3.5) のモデル関数の最小自乗フィッティングを行った結果得られた曲線が図1Bの実線になる。これにより,結合定数 \(K\) の値に加えて,\(\mathrm{M}\) または \(\mathrm{MX}\) のモル分率が 100% の時の吸光度 \(A_{\mathrm{M}}\) または \(A_{\mathrm{MX}}\) を算出することができる。ソフトウェアを用いた具体的な解析手順については,第5節を参照して頂きたい。
ここで一つ注意点を指摘しておくが,1波長の強度データの式 (3.5) による解析では,強度をとる波長は固定である。滴定実験中は,リガンド濃度の変化に伴ってピーク波長がシフトしていくかもしれないが,それに気をとられずに固定した波長から強度を取るべきである。なぜならば,式 (3.5) のモデル関数に含まれているパラメータ \(A_{\mathrm{M}}\) と \(A_{\mathrm{MX}}\) が定数という前提が含まれているからである。リガンド濃度変化に伴って,強度をモニターする波長を変えることは,この前提を破ることを意味する。
3.1.2. スペクトルからのモル分率の直読
反応 (3.1) のように蛋白質分子種が \(\mathrm{M}\), \(\mathrm{MX}\) の2種の場合には,それらのモル分率をスペクトルから直接読み取ることもしばしば行われている。実際,測定データの前処理法として,先輩の院生やスタッフからそのように習うという研究室も多いことであろう。図1Cに強度値の取り方を示す。この方法では,\(x = 0\) 時の強度を \(A_{1}\),\(x\) が十分高いときの強度を \(A_{2}\),そして任意のリガンド濃度 \(x\) のときの強度を \(A_{x}\) ととり,
\[ \frac{[\mathrm{M}]}{[\mathrm{M}] + [\mathrm{MX}]} = \frac{A_{2} - A_{x}}{A_{2} - A_{1}}, \mspace{10mm} \frac{[\mathrm{MX}]}{[\mathrm{M}] + [\mathrm{MX}]} = \frac{A_{x} - A_{1}}{A_{2} - A_{1}} \tag{3.6} \]
によって \(\mathrm{M}\) と \(\mathrm{MX}\) のモル分率を計算する[2]。実は,式 (3.5) を変形することによって,式 (3.6) と同様の形の式が得られる。
ここでは,\(A_{1}\), \(A_{2}\) がそれぞれ \(A_{\mathrm{M}}\), \(A_{\mathrm{MX}}\) に対する良い近似となっているか?ということ,そして,\(A_{1}\), \(A_{2}\) に測定誤差がどれだけ含まれているか?に注意する必要がある。実際,この方法では,\(A_{1}\), \(A_{2}\) の値が正確に決まったという前提に立ってモル分率を計算しているが,現実の実験では測定装置のノイズやドリフトもあればピペッティングの誤差もある。また,場合によっては,\(\mathrm{M}\) 型がモル分率 100% の強度および \(\mathrm{MX}\) 型 100% を実験的に測定できない場合もある(たとえば,pH 滴定では \(\ce{H+}\) 濃度がゼロや無限大になる前に蛋白質が変性するかもしれないし,あるいは解析対象外の別のコンフォメーションに変化するかもしれない)。以上のような点で問題なければ,式 (3.6) を使っても良いであろう。一方,式 (3.5) のモデル関数を用いた場合は,\(A_{\mathrm{M}}\), \(A_{\mathrm{MX}}\) の強度値もフィッティングで算出するので,ここで指摘したような気遣いの必要が減るという点で都合が良い。
さらに,スペクトルデータからモル分率を直接読み取った後,モル分率とリガンド濃度のデータを変換して線形プロットに載せるという手法も従来は広く行われてきた。たとえば,両逆数プロットは典型例である。モル分率の逆数をリガンド濃度の逆数に対してプロットする両逆数プロットに対応する関数を求めるために,式 (3.4) の両辺の逆数を取れば,
\[ \frac{1}{\alpha_{\mathrm{MX}}} = 1 + \frac{1}{K} \cdot \frac{1}{x} \tag{3.7} \]
であるので,両逆数プロットの傾きの逆数が結合定数となる。滴定実験のデータで線形プロットを用いる方法は,PC があまり普及していなかった時代にはよく使われた。しかし,昨今では一人一台で PC を使うことが普通になるとともに,グラフソフトウェア上の非線形フィッティングも手軽にできるようになったので,それらのプロット法はそれほど有用ではなくなった。もちろん,両逆数プロットを用いて1次関数で最小自乗フィッティングを行っても良いが,逆数をとることで各データポイントに含まれる測定誤差に偏りが発生することは覚えておく必要がある。その際には測定データの誤差もワークシートに入力し,各データポイントの測定誤差も含めて最小自乗フィッティングを行うと良いだろう。
3.1.3. リガンド濃度の取り扱い:遊離リガンド濃度,総リガンド濃度の選択
以上の計算で用いたリガンド \(\ce{X}\) の濃度 \(x\) は,あくまでも,反応 (3.1) におけるリガンドの分子種 \(\ce{X}\) の濃度である。つまり,\(x\) は,\([\ce{X}] + [\ce{MX}]\) ではなく,\([\ce{X}]\) なのである。同じことだが念を押せば,\(x\) は蛋白質に結合していない遊離したリガンド \(\ce{X}\) の濃度である。これは,\(\ce{H+}\) をリガンドとして pH メータで \(\ce{H+}\) を測定するときや,その他,酸素電極やイオン電極でリガンド濃度を測定するときは,測定器が表示する値をそのまま \(x\) としても良いだろう。また,pH 緩衝溶液や \(\ce{Ca^{2+}}\) 緩衝溶液のようにバッファーでリガンド濃度を固定するときも所定の濃度を \(x\) として良いだろう。しかし,いくつかの場合では,リガンド濃度の取り扱いには工夫が必要である。以下では,実験で遭遇しそうないくつかのケースについて説明する。ここで,測定溶液中に加えた総蛋白質濃度を \(\ce{[M]_{T}}\), 総リガンド濃度を \(\ce{[X]_{T}}\) と書くことにする:
\[ \ce{[M]_{T}} = \ce{[M]} + \ce{[MX]} \tag{3.8} \]
\[ \ce{[X]_{T}} = \ce{[X]} + \ce{[MX]} = x + \ce{[MX]} \tag{3.9} \]
【ケース1】\(1/K \gg \ce{[M]_{T}}\) の場合
\(\alpha_{\ce{MX}} = 1/2\) となるリガンド濃度 \(x\) が \(1/K\) であるので,滴定実験で用いる\(\ce{[X]_{T}}\) の範囲は \(1/K\) の前後付近をとるのが通常である(たとえば,\(0.1/K\) – \(10/K\) くらいの範囲)。つまり,このケースでは,実験で用いるリガンド総濃度 \(\ce{[X]_{T}}\) は,蛋白質総濃度 \(\ce{[M]_{T}}\) にくらべて十分に過剰である。したがって,良い近似で \(\ce{[X]_{T}} \approx x\) と見なして滴定曲線をとっても良い。
【ケース2】リガンド \(\ce{X}\) をバッファーで与える場合
pH 緩衝溶液や \(\ce{Ca^{2+}}\) 緩衝溶液等の緩衝溶液を使うことで遊離リガンド濃度 \(x\) をコントロールすれば,蛋白質との結合反応が起こっても遊離リガンド濃度の変動を低減することができる。このときも,バッファーを調製したときのリガンド濃度を \(x\) として滴定曲線を描いても良い。ただし,十分な濃度の緩衝剤を加えることにより,反応 (3.1) が起こっても遊離リガンド濃度 \(x\) の変動が解析上問題ない程度に小さいことを実験プロトコル上確認しておく必要があるだろう。試料溶液中のバッファー濃度が十分かどうかに気を遣うのは,蛋白質実験の常識・基本の一つである。
【ケース3】\(1/K \sim \ce{[M]_{T}}\),あるいは \(1/K < \ce{[M]_{T}}\) の場合
これは,リガンドの蛋白質に対する結合の親和性が高いケースである。この条件における滴定実験では,用いる遊離リガンド濃度 \(x\) や総リガンド濃度 \(\ce{[X]_{T}}\) を \(\ce{[M]_{T}}\) の前後やそれ以下にとることが必要であること,そして,試料溶液に加えた総リガンド量のうち,かなりの割合が蛋白質に結合するために \(x \approx \ce{[X]_{T}}\) という近似が使えない条件で測定になることに注意する。こういう注意点を看過してケース1と同様な \(x \approx \ce{[X]_{T}}\) という近似が可能だと勘違いをして式 (3.5) で解析をすると,解析結果にかなりの誤差を招いてしまう。
例題として,リガンドの蛋白質に対する結合の親和性が非常に高い状況(\(1/K \ll \ce{[M]_{T}}\))を思考実験することにしよう。この場合,リガンド \(\ce{X}\) の添加によって反応 \(\ce{M + X -> MX}\) が一方的に進む。滴定実験において \(\ce{X}\) の濃度を徐々に増やしながら \(\ce{[M]}\) と \(\ce{[MX]}\) を測定すると,\(\ce{[X]_{T}}\) が低いときは分子種 \(\ce{M}\) が支配的,\(\ce{[X]_{T}} = \ce{[M]_{T}}/2\) の時に \(\ce{[M]} = \ce{[MX]}\),そして \(\ce{[X]_{T}}\) をさらに増やしていくと分子種 \(\ce{MX}\) が支配的になって飽和する,という結果になる。こういう場合でも,測定強度を \(\ce{[X]_{T}}\) に対してプロットすると,いかにもモデル関数 (3.5) が適用できそうな形状のグラフが得られてしまう。ただし,このような滴定データにモデル関数 (3.5) を適用して解析すると,結合定数の解析値は \(K = 2/\ce{[M]_{T}}\) 前後となるであろう(つまり,こうして得られた \(K\) の解析値は,総蛋白質濃度 \(\ce{[M]_{T}}\) に依存する)。しかし,そのような解析値は結合定数の真の値を反映するものではない。特に親和性が高い場合の滴定実験では,非常に低い濃度のリガンドおよび蛋白質で,慎重を期したタフな滴定実験を行う必要があるが,ここで説明したようなことを忘れていると,頑張ってやったはずの滴定実験が単に \(2/\ce{[M]_{T}}\) といった蛋白質濃度を測っただけだったという残念な結果になりかねない。
このような問題点を解決する方法としては,以下が挙げられる:
- リガンドが低分子であれば,平衡透析を行い,透析内液で \(\mathrm{[M]}\),\(\mathrm{[MX]}\) を測定し,透析外液中のリガンド濃度を測定して \(x\) 値とする
- 蛋白質総濃度 \(\mathrm{[M]_{T}}\) に比べて,\(1/K\) 値がそれほど低くなければ,式 (3.5) のモデル関数の独立変数を \(\mathrm{[X]_{T}}\) とする変形を行うこともできる(下記参照)。
後者の場合,\(K\), \(\mathrm{[X]_{T}}\), \(\mathrm{[M]_{T}}\) から遊離リガンド濃度 \(x\) を与える関数と式 (3.5) を併せて使って最小自乗フィッティングを行っても良いだろう。すなわち,式 (3.2),(3.8),(3.9) より得られる解
\[ x = \frac{-\{1 + K(\mathrm{[M]_{T}} - \mathrm{[X]_{T}})\} + \sqrt{\{1 + K(\mathrm{[M]_{T}} - K\mathrm{[X]_{T}})\}^{2} + 4K\mathrm{[X]_{T}}}}{2K} \tag{3.10} \]
を式 (3.5) に代入すれば,\(\mathrm{[M]_{T}}\), \(\mathrm{[X]_{T}}\) を独立変数としたモデル関数を導出できる。
3.2. 2波長測定による解析(強度比による Ratiometry 解析)
2波長の強度比をとる測定は,蛋白質の濃度の変動や誤差をキャンセルできるという点で有用であり,分光光度計によるキュベット中での測定のみならず,蛍光顕微鏡観察でもしばしば使われている。Ratiometry 解析する際は,データの前処理や強度比をとる波長の選択で注意が必要である。本節ではこれら2点について説明する。
データの前処理で必要なことは,測定強度に含まれるバックグラウンドやオフセット値を差し引いて,蛋白質由来の正味の強度値を算出しておくことである。この前処理が必要な理由は,2.1節で説明した測定強度の線形性を確保することで,実測された強度比をモデル関数で適切に解析するためである。蛍光強度の場合は,試料やガラス等が由来の自家蛍光,測定装置内外からの迷光,そして光検出器の暗電流などがそのバックグラウンドの原因である。吸光度では,不純物や試料溶液の濁度などがバックグラウンドになる。また,顕微鏡観察で用いる EMCCD,sCMOS 等のカメラでは,暗電流に加えて,読み出される輝度にオフセットを一律に加算しているものもある。以上のように,生の測定値からバックグラウンド値やオフセット値を差し引いた後に強度比を計算し,さらに解析を行うのが正しい手順である。
次に,強度比を得るための2つの波長に選択について説明する。確かに,2つの波長の選択に際して注意を払わずに強度比をとったとしても,強度比のリガンド濃度 \(x\) の依存性はしばしば式 (3.5) と同様な曲線となる。しかし,強度比のプロットの解析において式 (3.5) のモデル関数をそのまま使ってフィッティングを行うと,算出される \(K\) の解析値は真の値からシステマティックにずれることがある。どこに問題があるのかを知るために,リガンド濃度 \(x\) に対する強度比のモデル関数を導出してみよう。図1Aにあるように,波長 \(\lambda_{1}\) の吸光度に加えて,波長 \(\lambda_{2}\) における吸光度をとり \(B(x)\) とする。\(\ce{M}\),\(\ce{MX}\) のモル分率が 100% の時の \(B\) の強度値をそれぞれ \(B_{\mathrm{M}}\), \(B_{\mathrm{MX}}\) とすると,式 (3.5) に相当する \(B\) のモデル関数は
\[ B(x) = B_{\mathrm{M}} \frac{1}{1 + Kx} + B_{\mathrm{MX}} \frac{Kx}{1 + Kx} \tag{3.11} \]
である。そこで,図1Dのように \(A/B\) 比をとると,
\[
\begin{align}
\frac{A(x)}{B(x)}
&=
\cfrac
{A_{\mathrm{M}} \cfrac{1}{1 + Kx} + A_{\mathrm{MX}} \cfrac{Kx}{1 + Kx}}
{B_{\mathrm{M}} \cfrac{1}{1 + Kx} + B_{\mathrm{MX}} \cfrac{Kx}{1 + Kx}}\
&=
\cfrac{A_{\mathrm{M}}}{B_{\mathrm{M}}} \cdot
\cfrac{1}{1 + \left( \cfrac{B_{\mathrm{MX}}}{B_{\mathrm{M}}} K \right) x} +
\cfrac{A_{\mathrm{MX}}}{B_{\mathrm{MX}}} \cdot
\cfrac{\left( \cfrac{B_{\mathrm{MX}}}{B_{\mathrm{M}}} K \right) x}{1 + \left( \cfrac{B_{\mathrm{MX}}}{B_{\mathrm{M}}} K \right) x}
\tag{3.12}
\end{align}
\]
を得る。よく見てみれば,これは,式 (3.5) と同様の形をしているが,結合定数に相当する項が異なる(分母同士を比較すれば分かる)。すなわち,式 (3.5) から (3.12) へ移行するにあたり,
\[ K \to \frac{B_{\mathrm{MX}}}{B_{\mathrm{M}}} K \tag{3.13} \]
という変換が(不本意にも)施されている。このことは,\(A(x)/B(x)\) をリガンド濃度 \(x\) に対してプロットしたデータに対して式 (3.5) のモデル関数で最小自乗フィッティングを行った場合,そこで得られる \(K\) 値は,真の結合定数値の \(B_{\mathrm{MX}}/B_{\mathrm{M}}\) 倍として算出されるということを意味する。図1Dに強度比のプロットを示すが,\(A/B\) 比の低濃度極限と高濃度極限の中間値となるリガンド濃度が,図1Bと一致していないことが分かるであろう。
このようなアーティファクトを避ける方法の一つとして,図1Aの \(\lambda_{\mathrm{iso}}\) のような等吸収点(isosbestic point)あるいは等発光点(isoemissive point; isolampsic point)を強度 \(B\) の波長にとることがあげられる。なぜなら,等吸収点や等発光点を \(B\) 値とすれば \(B_{\mathrm{M}} = B_{\mathrm{MX}}\) なので,式 (3.13) において \(K\) 値のシフトが発生しないからである。あるいは,強度比の補正を施した式 (3.12) で解析をすることでもアーティファクトを避けることができる。
3.3. リガンド結合に伴うアロステリック効果
以上の各節では,反応 (3.1) の蛋白質分子種 \(\ce{M}\) および \(\ce{MX}\) と,測定される強度 \(A_{\mathrm{X}}\),\(A_{\mathrm{MX}}\) が 1:1 に対応すると暗黙のうちに仮定してモデル関数の導出を行ってきた。たとえば,ミオグロビンの酸素平衡における吸光スペクトルは,酸素分子の結合解離と直接連動していると考えてもよいであろう。しかし,リガンド結合と測定強度との対応が間接的な場合もあるかもしれない。そこで本節では,測定強度の変化が,リガンド結合の直接的な効果ではなく,リガンド結合で誘起された蛋白質のコンフォメーション変化を反映したアロステリック効果[4]を含む場合について言及する。最も簡単なケースは以下のスキームであろう:
\[
\begin{array}{ccc}
\mathrm{M_{0}} & \to & \mathrm{M_{1}} \
\downarrow & & \downarrow \
\mathrm{M_{0}X} & \to & \mathrm{M_{1}X}
\end{array}
\tag{3.14}
\]
ここで,コンフォメーション0(\(\mathrm{M_{0}}\) と \(\mathrm{M_{0}X}\))はリガンド結合にかかわらず同じスペクトルを示し,コンフォメーション1(\(\mathrm{M_{1}}\) と \(\mathrm{M_{1}X}\))もリガンド結合にかかわらず同じスペクトルを示すが,コンフォメーション0と1ではスペクトルが異なると仮定する。この反応の諸定数は
\[
\begin{align}
^{0}K &= \frac{[\mathrm{M_{0}X}]}{[\mathrm{M_{0}}]x},
\mspace{10mm}
^{1}K = \frac{[\mathrm{M_{1}X}]}{[\mathrm{M_{1}}]x},
\tag{3.15}
\
L_{10} &= \frac{[\mathrm{M_{1}}]}{[\mathrm{M_{0}}]}
\tag{3.16}
\end{align}
\]
とする。以上を再編成した関係式
\[ \frac{\mathrm{M_{0}X}}{\mathrm{M_{0}}} = \, ^{0}Kx, \mspace{10mm} \frac{\mathrm{M_{1}X}}{\mathrm{M_{0}}} = L_{10} \, ^{1}Kx, \tag{3.17} \]
より,コンフォメーション0および1のモル分率 \(^{0}\alpha\),\(^{1}\alpha\) は,
\[
\begin{align}
^{0}\alpha
&= \frac
{[\mathrm{M_{0}}] + [\mathrm{M_{0}X}]}
{[\mathrm{M_{0}}] + [\mathrm{M_{0}X}] + [\mathrm{M_{1}}] + [\mathrm{M_{1}X}]}\
&= \frac
{1 + \, ^{0}Kx}
{1 + L_{10} + (^{0}K + L_{10} \, ^{1}K)x}
\tag{3.18}
\
^{1}\alpha
&= \frac
{[\mathrm{M_{1}}] + [\mathrm{M_{1}X}]}
{[\mathrm{M_{0}}] + [\mathrm{M_{0}X}] + [\mathrm{M_{1}}] + [\mathrm{M_{1}X}]}\
&= \frac
{L_{10} + L_{10} \, ^{1}Kx}
{1 + L_{10} + (^{0}K + L_{10} \, ^{1}K)x}
\tag{3.19}
\end{align}
\]
となるので,これらを式 (2.2) に適用することで以下のモデル関数を得ることができる:
\[ A(x) = \, ^{0}A \frac{1 + \, ^{0}Kx}{1 + L_{10} + (^{0}K + L_{10} \, ^{1}K)x} + \, ^{1}A \frac{L_{10} + L_{10} \, ^{1}Kx}{1 + L_{10} + (^{0}K + L_{10} \, ^{1}K)x} \tag{3.20} \]
ここで,\(^{0}A\),\(^{1}A\) は,それぞれコンフォメーション0,1のモル分率が 100% としたときの測定強度である。さらに,第1項,第2項の分数の分母を,\(1 + Kx\) の形に変形してまとめると,
\[
\begin{multline}
A(x) =
\frac{1}{1 + L_{10}} \times \
\shoveleft{
\left\{
(^{0}A + \, ^{1}AL_{10})
\cfrac{1}{1+ \cfrac{^{0}K + L_{10} \, ^{1}K}{1 + L_{10}}x} +
\cfrac{(1 + L_{10})(^{0}A^{0}K + ^{1}AL_{10} \, ^{1}K)}{^{0}K + L_{10} \, ^{1}K}
\cfrac{\cfrac{^{0}K + L_{10} \, ^{1}K}{1 + L_{10}}x}{1 + \cfrac{^{0}K + L_{10} \, ^{1}K}{1 + L_{10}}x}
\right\}
}
\tag{3.21}
\end{multline}
\]
と,式 (3.5) と同様な形に変形することができる。したがって,滴定曲線の形状のみから,スペクトル変化の原因がリガンド結合の直接的な効果なのか,あるいはリガンド結合に伴うアロステリック効果なのかは区別できない。また,式 (3.5) のモデル関数の形状が \(A_{\mathrm{M}}\),\(A_{\mathrm{MX}}\),\(K\) の3個のパラメータで規定されていることを考慮すれば,滴定曲線に対する式 (3.21) の最小自乗フィッティングだけで \(L_{10}\), \(^{0}K\),\(^{1}K\),\(^{0}A\),\(^{1}A\) をすべて一意に決定できない。それら5個のパラメータ値を決めるには,そのうち2個以上は別の実験で決めておく必要がある。また,このケースでは協同性はあらわれず,Hill 係数は1となる。
4. 1種類のリガンドで2個以上の結合部位をもつ蛋白質の解析
本節では,1種類のリガンドの結合部位が2個以上で,蛋白質がいくつかのコンフォメーションをとり,アロステリック効果を含む場合を説明する。この場合の一般的な反応スキームは,文献[4]に倣えば,以下のように書ける:
\[
\begin{array}{ccccccc}
\mathrm{M_{0}} & \to & \mathrm{M_{1}} & \to & \dotsm & \to & \mathrm{M}_{t}\
\downarrow & & \downarrow & & & & \downarrow\
\mathrm{M_{0}X} & \to & \mathrm{M_{1}X} & \to & \dotsm & \to & \mathrm{M}_{t}\mathrm{X}\
\downarrow & & \downarrow & & & & \downarrow\
\vdots & & \vdots & & & & \vdots\
\downarrow & & \downarrow & & & & \downarrow\
\mathrm{M}_{0}\mathrm{X}_{N} & \to & \mathrm{M}_{1}\mathrm{X}_{N} & \to & \dotsm & \to & \mathrm{M}_{t}\mathrm{X}_{N}
\end{array}
\tag{4.1}
\]
結合段階数 \(N\) や取り得るコンフォメーション数 \(t\) が多い場合や未知の場合は特に,このスキームにおける全ての平衡定数を実験的に決めることは困難であるため,より簡単化されたモデルがよく用いられる。ここでは,簡単化されたモデルとして,逐次結合反応と協同性反応について説明する。なお,多重平衡反応理論の詳細は本稿の範囲をはるかに超えるので,文献[2][4][5]を参照して頂きたい。
4.1. 逐次結合反応(Adair の式の応用)
簡単化の一つは,反応 (4.1) における結合リガンド数が同じ蛋白質分子種のコンフォメーションを1種類とするものである。すなわち,反応 (4.1) の1つの列だけが許されると考えるものである。たとえば,horse heart cytochrome c の pH 滴定[6]などはこのタイプに相当するであろう。この場合,リガンド結合の逐次反応
\[ \ce{M -> MX -> MX2 \dotsm -> MX_{\mathit{N}}} \tag{4.2} \]
を考えることになる。これについてモデル関数を導出する。まず,反応
\[ \ce{M + jX <=> MX_{j}} \tag{4.3} \]
に注目し,その結合定数 \(K_{j}\) を,
\[ K_{j} = \frac{[\mathrm{MX}_{j}]}{[\mathrm{M}]x^{j}} \tag{4.4} \]
とする。ここから,\(j\) 個のリガンドが結合した蛋白質分子種 \(\ce{MX_{j}}\) のモル分率を求める。式 (4.4) より \([\mathrm{MX}_{j}] = [M]K_{j}x^{j}\) なので,すべてのリガンド結合蛋白質分子種の濃度和は,
\[ \sum_{j}[\mathrm{MX}_{j}] = [M] \{1 + K_{1}x + K_{2}x^{2} + \dots + K_{N}x^{N} \} \tag{4.5} \]
と書ける。ここで,カギ括弧の中
\[ P = 1 + K_{1}x + K_{2}x^{2} + \dots + K_{N}x^{N} \tag{4.6} \]
は,結合多項式(binding polynomial)と呼ばれている[4][5]。これより,\(\mathrm{MX}_{j}\) のモル分率を \(\chi_{j}\) とすると,
\[ \chi_{j} = \frac{[\mathrm{MX}_{j}]}{\displaystyle \sum_{j}[\mathrm{MX}_{j}]} = \frac{K_{j}x^{j}}{1 + K_{1}x + K_{2}x^{2} + \dots + K_{N}x^{N}} = \frac{K_{j}x^{j}}{P} \tag{4.7} \]
が得られる。
測定強度のモデル関数を得るには,モル分率の式 (4.7) を式 (2.2) に適用すれば良い。そこで,蛋白質分子種 \(\ce{MX_{j}}\) がモル分率 100% の時の強度を \(A_{j}\) とすると,モデル関数として
\[ A_{\mathrm{model}}(x) = A_{0}\chi_{0} + A_{1}\chi_{1} + \dots + A_{N}\chi_{N} = \frac{1}{P} \left\{ A_{0} + A_{1}K_{1}x + \dots + A_{N}K_{N}x^{N} \right\} \tag{4.8} \]
を得る。歴史的にみると,これは Adair の式[7]の応用といえる。ここでは一般型を導出したが,現実問題としては,反応段階数は数段くらいが解析可能な範囲であろう。
4.2. 協同性反応(Hill の協同性の式の応用)
測定対象の蛋白質のリガンド結合部位が2個以上あるにもかかわらず,実験で得られた滴定曲線に変曲点が1個しか見あたらないとか,等吸収点や等発光点を持つというふうに2状態遷移に似たリガンド濃度依存性を示すことがある(たとえば,cytochrome c の pH 滴定[8][9]や,\(\ce{Ca^{2+}}\) センサー蛍光蛋白質[10])。そういう滴定実験のデータに対して,Hill の協同性の式[11]に倣ったモデル関数で解析することがしばしば行われている。これは,反応 (4.1) を
\[ \ce{M + nX <=> MN_{n}} \tag{4.9} \]
と近似し,蛋白質分子種としては \(\ce{M}\) と \(\ce{MX_{n}}\) の2つのみが存在するとみなしたモデル化である。ただし,\(n\) は整数に限らない。この場合,\(\ce{MX_{n}}\) のモル分率 \(\theta\) は,
\[ \theta = \frac{[\ce{MX_{n}}]}{[\ce{M}] + [\ce{MX_{n}}]} = \frac{(K_{\mathrm{H}}x)^{n}}{1 + (K_{\mathrm{H}}x)^{n}} \tag{4.10} \]
と書くことにする。これを式 (2.2) に適用して,
\[ A_{\mathrm{model}}(x) = D_{0}(1 - \theta) + D_{n}\theta = D_{0} \frac{1}{1 + (K_{\mathrm{H}}x)^{n}} + D_{n} \frac{(K_{\mathrm{H}}x)^{n}}{1 + (K_{\mathrm{H}}x)^{n}} \tag{4.11} \]
と,測定強度のモデル関数を得ることができる。このモデルを使った解析例を図4に示す(詳細は第5節を参照)。ここで,\(D_{0}\),\(D_{n}\) は,強度のリガンド低濃度極限と高濃度極限である。Hill プロットは,\(\theta / (1 - \theta)\) の対数を \(x\) の対数に対してプロットしたものであり,Hill プロットの傾きが Hill 係数である。この場合の Hill 係数は,もちろん,
\[ n_{\mathrm{H}} = \frac{\partial}{\partial \ln x} \left( \ln \frac{\theta}{1 - \theta} \right) = n \tag{4.12} \]
であるので,反応 (4.9) における \(n\) 値が Hill 係数となる。ただし,一般的にはリガンド濃度が低い領域および高い領域では,実際の滴定データの Hill プロットの傾きは1に近づくが[4],式 (4.10) のモデルにおける Hill プロットの傾きはリガンド濃度全域で \(n\) となる点では,実測値とモデル曲線には多少の差異が生じる。
実のところ,反応 (4.9) および式 (4.10) のモデルにおける Hill 係数の具体的な物理的意味はあまり明らかではない。実際,同じ蛋白質についてモデル化した反応 (4.9) の \(n\) と,反応 (4.2) の全段階数 \(N\) については,\(n \le N\) という制約は存在するが,\(n\) と \(N\) は必ずしも一致しない。ただし,具体的なメカニズムを盛り込めば,Hill 係数の物理的な意味を直感的に理解しやすくなることもある。以下でその一例を示す。
蛋白質が2つのコンフォメーションをとり,それらの間の平衡がリガンド \(\ce{X}\) によってシフトするというモデルを考える:
\[
\begin{array}{ccc}
\ce{M0} & \to & \ce{M1}\
\downarrow & & \downarrow\
\ce{M0X} & \to & \ce{M1X}\
\downarrow & & \downarrow\
\vdots & & \vdots\
\downarrow & & \downarrow\
\ce{M0X_{\mathit{N}}} & \to & \ce{M1X_{\mathit{N}}}
\end{array}
\tag{4.13}
\]
ここでの強度測定は,リガンド結合数は検出できないが,コンフォメーション0と1を区別して検出できるものとする。これは,3.3節のモデルを,多段階リガンド結合に拡張したものである。例えば,2個以上の水素イオン,2価の陽イオン,あるいは変性剤等の結合解離でコンフォメーション変化が起こり,その結果起こるスペクトル変化をモニターしている場合に相当する。そこで,リガンド結合数に依らずコンフォメーション1全体のモル分率を \(\theta\) ととることにする:
\[ \theta = \frac {\displaystyle \sum_{k}[\ce{M1X_{\mathit{k}}}]} {\displaystyle \sum_{j=0,1}\sum_{k}[\ce{M_{\mathit{j}}X_{\mathit{k}}}]}, \mspace{10mm} 1 - \theta = \frac {\displaystyle \sum_{k}[\ce{M0X_{\mathit{k}}}]} {\displaystyle \sum_{j=0,1}\sum_{k}[\ce{M_{\mathit{j}}X_{\mathit{k}}}]} \tag{4.14} \]
これらモル分率を使うと,Hill プロットの縦軸は
\[ \ln \frac{\theta}{1 - \theta} = \ln \frac {\displaystyle \sum_{k}[\ce{M1X_{\mathit{k}}}]} {\displaystyle \sum_{k}[\ce{M0X_{\mathit{k}}}]} \tag{4.15} \]
である。この右辺は
\[ K_{01} = \frac {\displaystyle \sum_{k}[\ce{M1X_{\mathit{k}}}]} {\displaystyle \sum_{k}[\ce{M0X_{\mathit{k}}}]} \tag{4.16} \]
の対数,すなわちコンフォメーション0,1間の平衡定数の対数になっている。よって,Hill プロットの傾きである Hill 係数は,
\[ n’_{H} = \frac{\partial \ln K_{01}}{\partial \ln x} \tag{4.17} \]
である。実は,平衡定数の対数 \(\ln K_{01}\) を \(\ln x\) に対してプロットしたものは,「Wyman プロット」と呼ばれるものに相当しており,そのプロットの曲線の微係数は遷移に伴うリガンド結合数の差分であることが知られている[4][5]:
\[ n’_{\mathrm{H}} = \frac{\partial \ln K_{01}}{\partial \ln x} = \bar{X}_{1}(x) - \bar{X}_{0}(x) = \Delta \bar{X}(x) \tag{4.18} \]
ここで,\(\bar{X}_{0}(x)\),\(\bar{X}_{1}(x)\) は,リガンド濃度が \(x\) である時のコンフォメーション0, 1のリガンド結合数(コンフォメーション0あるいは1をとる蛋白質1モルあたりに結合しているリガンドのモル数)である。すなわち,ここで議論したモデルにおいては,Hill 係数はコンフォメーション変化前後のリガンド結合数の差に相当する。式 (4.18) の導出と意味は,本稿末尾の補足で説明する。
5. 解析例
5.1. 1個のリガンド結合反応
本節では,1個のリガンド結合部位を持つ蛋白質の反応 (3.1) を解析した例題を示す。最初に結果を示し,次いでグラフ作成・データ解析ソフトウェアである ORIGIN で実際に最小自乗フィッティングを行ったスナップショットを参照しながら,具体的なフィッティングの手順を例示する。
5.1.1. 1 個のリガンド結合反応の解析結果
図1Aに示した吸光スペクトルデータは,例示の目的で筆者がコンピュータ上で作成したものである。分子種 \(\ce{M}\) と \(\ce{MX}\) の吸光スペクトル曲線と \(K = 1 \times 10^{5} \, \mathrm{M}^{−1}\) を与えて,式 (3.5) のモデル関数に誤差として乱数を加えて生成した。スペクトルから波長 \(\lambda_{1}\) における吸光度を抽出し,リガンド濃度 \(x\) に対してプロットしたのが図1Bである。この例題では反応メカニズムの答えを反応 (3.1) だと知っているので,解析には式 (3.5) を用いることにした。式 (3.5) を最小自乗法で図1Bのプロットに対してフィッティングした結果,実線の軌跡が得られ,結合定数の解析値は,\(0.997 \times 10^{5} \, \mathrm{M}^{−1}\) となった(これは乱数を加えたデータを使ったモンテカルロシミュレーションなので,もちろん,異なるデータセットを使う度に解析値に多少の変動がある)。
解析においては,図1Bでプロットすべき吸光度の波長について迷うかもしれない。ここでは,分子種 \(\ce{M}\) と \(\ce{MX}\) との吸光度差が大きいことを理由に波長 \(\lambda_{1}\) を選んだ。実際の測定データの解析においては,(1) 試料分子の分光学的性質に照らし合わして解析対象の現象を反映した強度変化が得られる波長,(2) リガンド,共溶媒,コンタミネーション等からの妨害がない波長,(3) 測定ノイズの少ない波長,そして (4) 強度変化の幅が大きい波長,などを指標にモニター波長を選ぶと良いであろう。
5.1.2. データ解析ソフトウェアを用いた実際の解析手順
この節では,筆者が使っているデータ解析・グラフ作成用ソフトウェアの ORIGIN(OriginLab, Northampton, MA, USA;Windows 版)を使った解析手順の概要を紹介する。非線形最小自乗フィッティングは,
- モデル関数の作成
- モデル関数のデータに対するフィッティング計算
の2つの手順から構成される。ORIGIN のスクリーンショットを参照しながら解析の流れを見ていくことにする。まず,ORIGIN を起動し,フィッティング対象のデータを表示しているグラフ窓をクリックしてアクティブ化して,メニューバーに「解析」を表示させる。さらに,メニューバーより「解析→フィット→非線形曲線フィット」を起動して(図2A),「NL Fit」窓を開く。
モデル関数の作成では,モデル関数のファイル名の指定,変数名の指定,そしてモデル関数の数式入力等を行う。「NL Fit」窓からユーザー定義関数の「フィット関数の新規作成」ボタンを押して「フィット関数ビルダー」窓を開く(図2B)。関数名を記入し,「変数とパラメータ」窓に入り,独立変数(リガンド濃度),従属変数(吸光度),そしてパラメータの変数名を指定する(図2C)。図2Cでは,式 (3.5) のパラメータ \(A_{\mathrm{M}}\),\(A_{\mathrm{MX}}\),\(K\) はこの窓内ではそれぞれ A_M,A_MX,K,従属変数を y,独立変数を x とした。設定を進めて,図2Dの「式形式の関数」窓では,「関数内容」欄に数式を記入する。さらに,必要があれば,それ以降の窓でパラメータの範囲等の諸条件も入力する。以上で,モデル関数の入力を完了する。
フィッティングは,モデル関数の選択,データの選択,パラメータの初期値設定,そしてフィッティング計算の順で行う。「NL Fit」窓から,カテゴリと関数を選択し(図3A),さらに解析対象のデータ選択が正しく行われているかを確認する。ORIGIN では,解析対象データをプロットしたグラフ窓をアクティブにしてからフィッティングを起動させると,それが解析対象データとして自動的に選択される(あるいは,「NL Fit」窓から解析対象のワークシート・カラムを設定してもよい)。次に,「Parameters」タブを選択し,パラメータの推測値(初期値)を設定する(図3B左)。最小自乗法のアルゴリズムとして広く使われている Levenberg-Marquardt 法では,予め設定されたパラメータの初期値を出発点として最適解を探す。最適解に近い推測値を設定してやると,異常解を避けて正常な最適解へ収束させやすい。式 (3.5) のモデル関数は,各パラメータの推測値をグラフ上から読み取りやすいように定式化している(図1E)。推測値を入力したら「\(\chi^{2}\)」ボタンを押し,入力したパラメータを初期値としたときのモデル曲線をグラフ上に描かせて確認する(図3B右)。モデル曲線がグラフ上に現れなかった場合,入力した数式に文法エラーがあったり,パラメータの初期値が最適値から遠かったりする可能性がある。さらに,フィッティングボタンを押すと,パラメータ値が収束条件に達するまで最適化計算を繰り返し,最終的に最適解を得る(図3C)。図3Dに表示したグラフによれば,モデル曲線はデータによく合ってようである。
最小自乗フィッティングは,ORIGIN の他にも,KaleidaGraph(Synergy Software, Reading, PA, USA)等のソフトウェアの非線形最小自乗フィッティングツールで式 (3.5) をユーザー定義関数として入力してやれば,行うことができる。これらのソフトウェアは,フィッティング計算に加えて計算結果をグラフ表示する機能が標準装備されているので便利である。その他にも,無料で配布されている gnuplot,C++ や FORTRAN で使用する数値計算ライブラリである IMSL(Rogue Wave Software, Louisville, CO, USA)や NAG Library(Numerical Algorithms Group, Oxford, UK),そして数学計算ソフトウェアの Mathematica(Wolfram Research, Champaign, IL, USA),MAPLE(Maplesoft, Waterloo, Canada),Matlab(MathWorks, Natick, MA, USA)等でもフィッティング計算が可能である。
5.2. シトクロム c の pH 滴定データ解析の実施例
本節では,筆者が実施した緑膿菌(Pseudomonas aeruginosa)のシトクロム c551(PA Cyt c)の pH 滴定実験[8]で得られたデータの解析例を説明する。この実験では,PA Cyt c の吸光スペクトルを pH 0.15–7.6 の範囲で測定することで,pH 変化に伴うコンフォメーションの変化をモニターした。その測定データに対して,モデル化と非線形最小自乗フィッティングを行うことで,水素イオンの PA Cyt c に対する結合定数や Hill 係数を求めた。
5.2.1. 生データからの定性的な情報の読み取り
フィッティング解析を始める前に,まずは実験データを眺めて,PA Cyt c のコンフォメーション変化について定性的な情報を読み取ることにする。図4AにPA Cyt c の吸光スペクトルの pH 変化を示す。また,図4Bには,代表的な波長として 532 nm の吸光度の pH に対するプロットを示す。これらのデータから以下のことに気づく:
- 図4Aより,低 pH 側および高 pH 側においてそれぞれ特異的な吸光スペクトルがあり、pH 変化に伴って吸光スペクトルがそれらへ漸近している(それぞれ,酸性型,中性型と呼ぶことにする)
- 図4Aにおいて,483, 509, 589, 648 nm に等吸収点がある
- 図4Bのプロットにおいて,酸性型と中性型との中点以外には,変曲点は見当たらないようだ
- 図4Bの吸光度変化の傾きから察するに,Hill 係数は1より大きいかもしれない
PA Cyt c が酸性および中性 pH で特異的な吸光スペクトルをもつことより,吸光スペクトルで類別される酸性型,中性型のコンフォメーションが存在していると解釈できる。また,等吸収点があることより,酸性型・中性型の2つのコンフォメーション間の遷移は,2状態遷移だと示唆される(すなわち,これら2状態間の遷移において,検出可能なモル分率を示す PA Cyt c の分子種は,酸性型および中性型の2種のみだと示唆される)。逆に,もしも吸光スペクトルが酸性型・中性型と異なる第3の吸光スペクトルを持つコンフォメーションが検出可能なモル分率で存在しているとすれば,等吸収点は存在しないであろう(より詳しくは,「(吸光スペクトルで類別される)酸性型・中性型間の遷移が2状態遷移かつそれらの吸光スペクトルに交わる点が存在するならば,等吸収点をもつ」は成り立つが,その逆の「等吸収点をもつならば,その遷移は2状態遷移である」は成り立つ場合もあれば成り立たない場合もある)。等吸収点に加えて,図4Bで酸性型・中性型の中点以外に変曲点が見られないことも,2状態遷移であることを支持している。
5.2.2. Hill の協同性モデルによる PA Cyt c のコンフォメーション遷移の解析
5.2.1節で読み取った情報をまとめれば,PA Cyt c は,特異的な吸光スペクトルを示す酸性型と中性型の2つのコンフォメーションをもち,これらのコンフォメーションのモル分率が pH に依存していると解釈された。また,酸型・中性型の間の遷移は,Hill 係数が1より大きい正の協同性が示唆された。以上より,Hill の協同性のモデルである式 (4.11) のモデル関数で,このコンフォメーション変化を記述できそうである。また,逆に,最小自乗フィッティング解析を行うことで,式 (4.11) のモデルが実験データを良く記述できるかどうかを確かめることができる。
図4Bの pH に対する吸光度のプロットに対して,式 (4.11) のモデル関数の最小自乗フィッティングを行った。ソフトウェアの操作手順は5.1.2節で説明したものと同様である。フィッティングによって,実測の吸光度のプロットによく合うモデル曲線を得ることができた(図4Bの実線)。これによって得られた最適解は,\(K_{\mathrm{H}} = 68.7 \, \mathrm{M}^{−1}\)(水素イオンの解離の pK に換算すると,1.83),\(n = 2.06\) と得られた。また,モデル曲線が実測値によく合っていることより,この解析で用いた Hill の協同性の2状態遷移モデルは,PA Cyt c の pH 依存性のコンフォメーション変化を良く記述しているようである。
5.2.3. Wyman プロットによる解析
さらに,4.2節で触れた Wyman プロットを PA Cyt c が中性型から酸性型へのコンフォメーション変化に適用した例を示す。Wyman プロットは,平衡定数の対数をリガンド濃度の対数に対してプロットしたものである。酸性型,中性型の分子種をそれぞれ \(\ce{M_{A}}\),\(\ce{M_{N}}\) と書くことにし,\(\mathrm{pH} = x\) における \(\ce{M_{A}}\) のモル分率を \(θ(x)\) とすると,
\[ \theta(x) = \frac{[\ce{M_{A}}]}{[\ce{M_{A}}] + [\ce{M_{N}}]}, \mspace{10mm} 1 - \theta(x) = \frac{[\ce{M_{N}}]}{[\ce{M_{A}}] + [\ce{M_{N}}]} \tag{5.1} \]
である。また,\(\ce{M_{A}}\),\(\ce{M_{N}}\) の平衡定数を \(K_{\mathrm{NA}}\) とすると
\[ K_{\mathrm{NA}}(x) = \frac{[\ce{M_{A}}]}{[\ce{M_{N}}]} = \frac{\theta(x)}{1 - \theta(x)} \tag{5.2} \]
となる。また,式 (4.11) の \(A_{\mathrm{model}}\) を測定値 \(A_{\mathrm{meas}}\) に入れ替え,\(D_{0}\),\(D_{n}\) は5.2.2節のフィッティング解析で得られた値を使うことにすれば,測定値から得られる \(\ce{M_{A}}\) のモル分率 \(\theta(x)\) は,
\[ \theta(x) = \frac{A_{\mathrm{meas}}(x) - D_{0}}{D_{n} - D_{0}} \tag{5.3} \]
となる。したがって,平衡定数 \(K_{\mathrm{NA}}\) の測定値は,
\[ K_{\mathrm{NA}}(x) = \frac{\theta}{1 - \theta} = \frac{A_{\mathrm{meas}}(x) - D_{0}}{D_{n} - A_{\mathrm{meas}}(x)} \tag{5.4} \]
で計算できる(再確認するが,\(K_{\mathrm{NA}}\) は PA Cyt c の2つのコンフォメーション間の平衡定数で,pH の関数である。PA Cyt c と水素イオンの結合定数 \(K_{\mathrm{H}}\)とは異なる)。以上より,\(\log_{10}K_{\mathrm{NA}}\) を \(\log_{10}[\ce{H+}]\)(\(= −\mathrm{pH}\))に対してプロットした Wyman プロットが得られる(図4C)。図4Cによれば,\(\log_{10}[\ce{H+}]\) が \(\log_{10}(1/K_{\mathrm{H}}) = −1.83\) の付近ではプロットがほぼ直線となり,1次関数のフィッティングによってその傾きは2.12と得られた。したがって,式 (4.18) より,図4Cで表示している pH 1–3 の範囲では,PA Cyt c の中性型→酸性型のコンフォメーション変化に伴う水素イオンの結合数変化の解析値は \(\Delta \bar{X} = 2.12\) 個という結果となった。
4.2節で説明したが,PA Cyt c の pH 変化に伴うコンフォメーション変化の Hill プロットも \(\log_{10}[\theta / (1 - \theta)]\) を \(\log_{10}[\ce{H+}]\) に対してプロットしたものであるので,結局のところ図4Cは Hill プロットでもある。したがって,Wyman プロットで得られた水素イオンの結合数変化 \(\Delta\bar{X} = 2.12\) と5.2.2節の Hill 係数 \(n = 2.06\) の値が近かったのは,偶然ではなく,解析に用いたモデルの上では近い内容のパラメータだったからである(Hill の協同性モデル式 (4.10) ではフィッティング範囲全域において \(n\) を定数とすることがモデルに含まれていたのに対し,Wyman プロットで得られる \(\Delta\bar{X}\) は単に Wyman プロット上の曲線の微係数としている点で,違いがある)。これらの2つの数値の間に発生した小さい差異は,用いたモデル関数やデータ範囲の違いによるものであると考えられる。
6. おわりに
多くの大学院生や研究者にとって,質量作用の法則は高校の化学で習う初歩的な事項であろう。そのため,多くの研究室では平衡定数を用いた諸計算は既知のことと見なされているようにも思われる。そういう事情が,質量作用の法則から開始し本稿の内容に至るような蛋白質平衡反応解析の基本原理の解説が実験書等でもあまり見られない理由かもしれないというのが,筆者の印象である。また,研究室の実験・解析の現場で,原理の理解はさておき,とにかくデータをコンピュータに入力して何らかの解離定数の数値を出せば良いという姿勢でもしも解析が進められているのであれば,本稿で指摘したようないくつかの誤りに陥ってしまうかもしれない。筆者からのメッセージのひとつは,実験者がデータ解析のためのモデルを立てる時は,実験データを処理するための数式の準備を隅々まで労を惜しまず自分の手で紙の上(あるいは,表計算ソフト,数式エディタ,数式処理ソフトウェア等でもよい)でやってみることが,実験対象の蛋白質が示す現象についてのアイディアを整理し,実験者の意図に沿って間違いなくデータ解析するのにしばしば有用である,ということである。本稿が,蛋白質の平衡反応解析の指導や実施の一助となれば幸いである。
補足. Wyman プロットの傾きについて
式 (4.18) は,2つのコンフォメーション間の遷移に伴う,蛋白質に結合しているリガンド数の変化を与えるものである。その内容を理解した気になるには,やはり,その式の導出過程をたどることが有効である。しかし,文献[4]や[5]に精通している読者ならともかく,蛋白質の平衡理論に精通していない多くの読者にとっては,それらの文献の中から導出過程を見つけて読み取るのは,あまり容易ではない。そこで,興味を持つ読者への便宜として,式 (4.18) の導出を説明することにする。
ここでの目標は,反応 (4.13) を基にして,蛋白質 \(\ce{M}\) のコンフォメーション0と1間の平衡定数のリガンド濃度依存性から,式 (4.18) を導出することである。\(\ce{M}\) と \(\ce{X}\) の平衡定数を
\[ K^{i}_{j} = \frac{[\ce{M_{\mathit{i}}X_{\mathit{j}}}]}{[\ce{M_{\mathit{i}}}]x^{j}}, \mspace{5mm} (i = 0, 1) \tag{A.1} \]
とする。インデックス \(i\) が \(\ce{M}\) のコンフォメーションを表している。各コンフォメーションの結合多項式は,
\[ P_{i} = \frac{1}{[\ce{M_{\mathit{i}}}]} \{ [\ce{M_{\mathit{i}}}] + [\ce{M_{\mathit{i}}X}] + \dots + [\ce{M_{\mathit{i}}X_{\mathit{N}}}] \} = 1 + K^{i}_{1}x + K^{i}_{2}x^{2} + \dots + K^{i}_{N}x^{N} \tag{A.2} \]
である。ここで,\(N\) は蛋白質1個あたりのリガンド結合部位数である(ただし,\(N\) は蛋白質が実際に持っている結合部位数より大きく取っても構わない。なぜなら,実際に起こらない反応段階については,結合定数を0としておくと考えれば,以下の導出過程に支障はないからである)。1モルあたりの \(\ce{M_{\mathit{i}}}\) に対して結合したリガンド \(\ce{X}\) のモル数 \(\bar{X}_{i}\) はリガンド濃度 \(x\) の関数であり,結合多項式を使って
\[
\begin{align}
\bar{X}_{i}
&= \frac
{1 \cdot [\ce{M_{\mathit{i}}X}] + 2 \cdot [\ce{M_{\mathit{i}}X_{2}}] + \dots + N \cdot [\ce{M_{\mathit{i}}X_{\mathit{N}}}]}
{[\ce{M_{\mathit{i}}}] + [\ce{M_{\mathit{i}}X}] + \dots + [\ce{M_{\mathit{i}}X_{\mathit{N}}}]}\
&= \frac
{K^{i}_{1}x + 2 \cdot K^{i}_{2}x^{2} + \dots + N \cdot K^{i}_{N}x^{N}}
{1 + K^{i}_{1}x + K^{i}_{2}x^{2} + \dots + K^{i}_{N}x^{N}}\
&= \frac
{\partial \ln P_{i}}
{\partial \ln x}
\end{align}
\tag{A.3}
\]
と書ける。よって,式 (A.2),(A.3) を使って式 (4.18) の微係数を計算すると,
\[
\begin{align}
\frac{\partial \ln K_{01}}{\partial \ln x}
&=
\frac{\partial}{\partial \ln x}
\left\{
\ln
\frac
{[\ce{M_{1}}] + [\ce{M_{1}X}] + \dots + [\ce{M_{1}X_{\mathit{N}}}]}
{[\ce{M_{0}}] + [\ce{M_{0}X}] + \dots + [\ce{M_{0}X_{\mathit{N}}}]}
\right\}\
&=
\frac{\partial}{\partial \ln x}
\ln
\frac
{[\ce{M_{1}}] \left( 1 + K^{1}_{1}x + \dots + K^{1}_{N}x^{N} \right)}
{[\ce{M_{0}}] \left( 1 + K^{0}_{1}x + \dots + K^{0}_{N}x^{N} \right)}\
&=
\frac{\partial \ln P_{1}}{\partial \ln x} - \frac{\partial \ln P_{0}}{\partial \ln x}\
&=
\bar{X}_{1}(x) - \bar{X}_{0}(x)
\end{align}
\tag{A.4}
\]
を得る。ここで,アポ型同士の反応商 \([\ce{M_{1}}]/[\ce{M_{0}}]\) は \(x\) に依存しない平衡定数となるので,微分をとることで消去されることも利用している。式 (A.4) の内容を読み込めば,リガンド濃度が \(x\) の時における,1モルあたりのコンフォメーション1の蛋白質に結合するリガンドのモル数と,1モルあたりのコンフォメーション0に結合するリガンドのモル数の差を,最後の行が表している。また,質量作用の法則を適用できる結合反応系であれば,各反応段階の結合定数の詳細な情報がなくても,コンフォメーション0,1間の平衡定数のリガンド濃度依存性の情報だけでリガンドの結合数の差分を求めることができるというのが,Wyman の理論から得られる式 (A.4) の効用である。
文献
- Germond, A. et al, Biophys. Rev. 8, 121–138 (2016)
- Klotz, I.M., Ligand-receptor energetics. Wiley & Sons, New York (1997)
- Cantor, C.R. & Schimmel, P.R., Biophysical Chemistry II: Techniques for the study of biological structure and function. W.H. Freeman, San Francisco (1980)
- Wyman, J. & Gill, S. J., Binding and linkage. University Science Books, Mill Valley (1990)
- Wyman, J., Adv. Protein Chem. 19, 223–286 (1964)
- Myer, Y.P. & Saturno, A.F., J. Protein Chem. 10, 481–494 (1991)
- Adair, G.S. et al., J. Biol. Chem. 63, 529–545 (1925)
- Wazawa, T. et al., Biophys. Chem. 151, 160–169 (2010)
- Miyashita, Y. et al., Biophys. J. 104, 163–172 (2013)
- Horikawa, K. et al., Nat. Methods 7, 729–732 (2010)
- Hill, A.V., J. Physiol. (suppl), 40, iv–vi (1910)
-
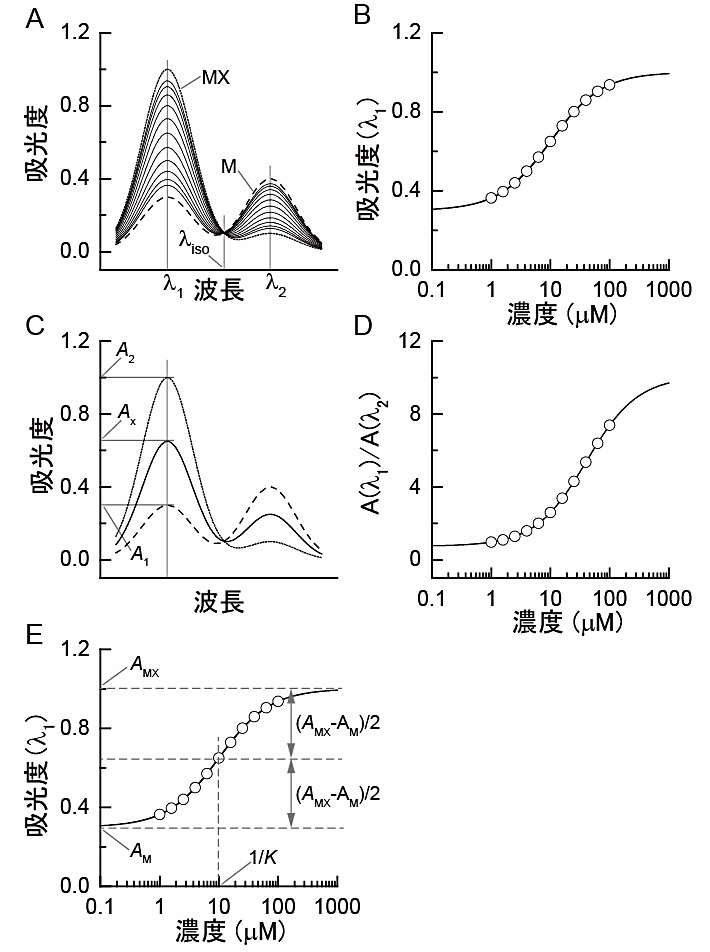
図1:シミュレーションで生成したスペクトルデータによるリガンド結合平衡反応の解析の例。(A)スペクトルのリガンド濃度依存性のシミュレーション。筆者が作成した分子種 M および MX のスペクトルを用いた式 (3.5) の関数に乱数を加えることで,x = 1 - 100 μM のスペクトルを生成した。また,ここでは,K = 1 × 105 M−1 としてデータを生成した。λiso は等吸収点。(B)リガンド濃度に対する波長 λ1 における吸光度のプロット。実線は最小自乗フィッティングの結果得られたモデル曲線。フィッティングからは,K = (0.997 ± 0.003) × 105 M−1 と算出された。(C)吸光スペクトルのグラフからのモル分率の直接の読み取り。(D)吸光度比の,リガンド濃度に対するプロット。実線は最小自乗フィッティングの結果。式 (3.13) における BMX/BM 比は0.25 (< 1) であるため,この滴定曲線はパネル(B)よりも高濃度側にシフトしている。(E)最小自乗フィッティングにおける初期値を選ぶときの方針。変数名は,式 (3.5) に合わせた。 -

図2:Origin ソフトウェアによる図1Bの最小自乗フィッティングにおけるモデル関数の定義のスクリーンショット。(A)非線形最小自乗フィッティングの起動。(B)関数名および関数形式の入力窓。(C)変数名・パラメータ名の入力窓。(D)モデル関数の数式の入力窓。 -
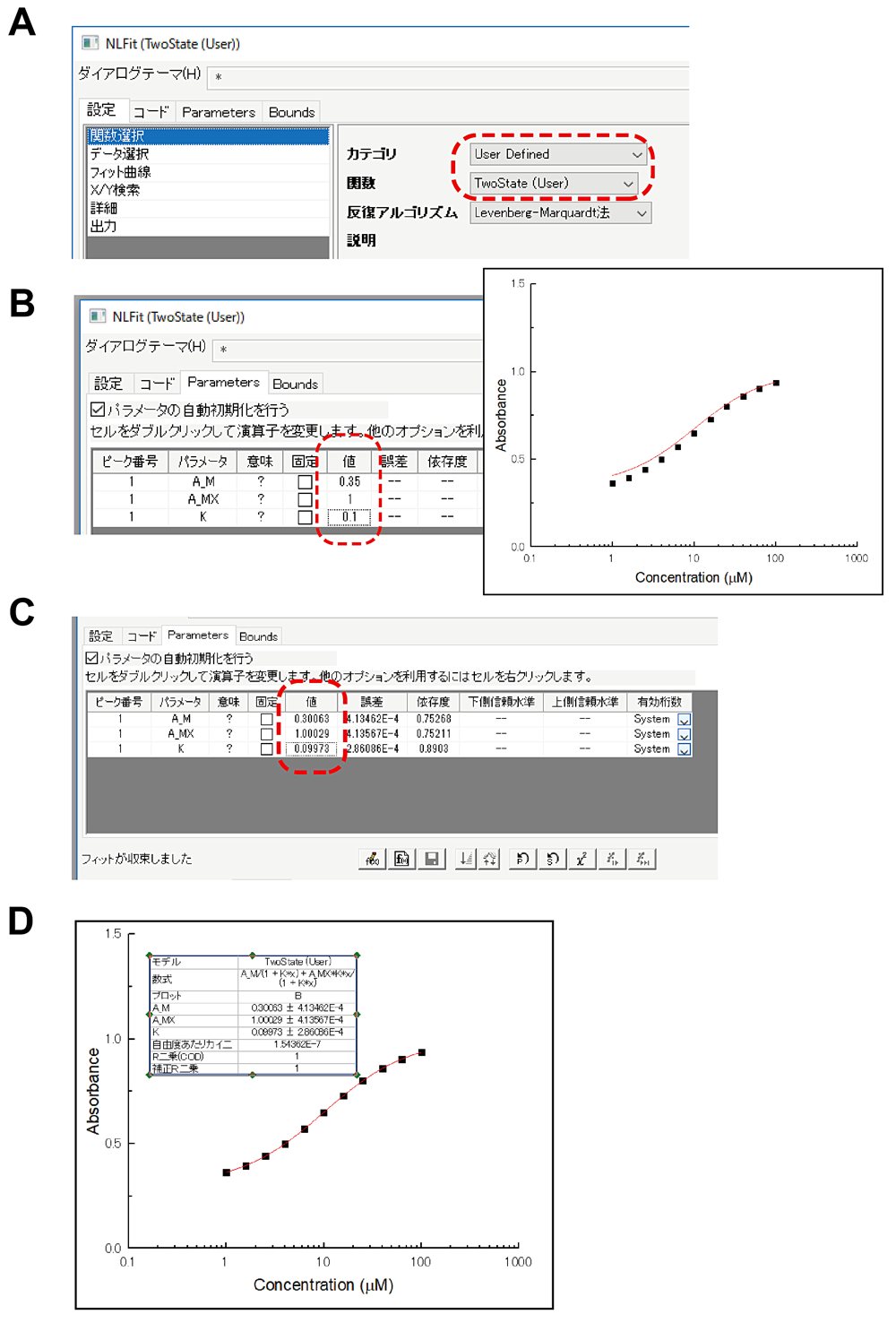
図3:Origin ソフトウェアによる図1Bの最小自乗フィッティングのスクリーンショット。(A)使用関数やデータを指定するため窓。(B)パラメータの初期値の入力窓と,初期値で描かせたモデル関数曲線。(C)フィッティングの結果のパラメータ値の表示。(D)計算結果のモデル曲線と入力データのプロット。 -
![図4:PA Cyt c の吸光スペクトルの pH 変化の解析例。(A)PA Cyt c(III) の可視光域の吸光スペクトル。pH 0.15‒7.6 の範囲で測定した。温度は20.0°C。許諾を受けて文献[8]から転載。(B)PA cyt c の 532 nm における吸光度の pH 変化と,それに対するフィッティングで得られた式 (4.11) のモデル曲線。許諾を受けて文献[8]から転載。(C)pH で誘起された PA Cyt c のコンフォメーション変化についての Wyman プロット。log_10_[H~+~]が−3から−1の範囲のデータに対してフィットさせた直線も表示した。この直線の傾きは2.12である。](/archives/images/photo_1/photo_1_Fig_04.png)
図4:PA Cyt c の吸光スペクトルの pH 変化の解析例。(A)PA Cyt c(III) の可視光域の吸光スペクトル。pH 0.15‒7.6 の範囲で測定した。温度は20.0°C。許諾を受けて文献[8]から転載。(B)PA cyt c の 532 nm における吸光度の pH 変化と,それに対するフィッティングで得られた式 (4.11) のモデル曲線。許諾を受けて文献[8]から転載。(C)pH で誘起された PA Cyt c のコンフォメーション変化についての Wyman プロット。log10[H+]が−3から−1の範囲のデータに対してフィットさせた直線も表示した。この直線の傾きは2.12である。
概要
蛋白質のリガンド結合反応やコンフォメーション変化は,蛋白質が機能するための重要なプロセスである。多くの場合,これらの実測には吸光測定や蛍光測定が用いられる。実測されたデータから平衡定数等のパラメータを算出するためには,最小自乗フィッティングによる解析が用いられる。吸光測定・蛍光測定の原理や化学熱力学・平衡論については講義や実験のチュートリアル等で話を聴く機会も多い。しかし,測定データと平衡論を組み合わせて数学的に展開するデータ解析手法の原理については,まとまった解説を聴く機会は少ないかもしれないし,あるいは解析は全てコンピュータ任せという人も多いかもしれない。しかし,複雑な結合様式やコンフォメーション変化を測定データの中から見いだすためには,データ解析の原理の理解が不可欠である。そこで,本稿では,解析原理,特に測定データ解析のためのモデル関数をどのように導出するかに重点を置いて解説する。具体的には,蛋白質における1種リガンドの結合平衡反応の吸光測定や蛍光測定データを解析するための原理,そして解析のためのモデル関数の導出の仕方について解説し,さらに解析時の注意点についても指摘する。
1. はじめに
蛋白質が機能し,動作するときには,他の分子との結合やコンフォメーション変化が伴う。このため,蛋白質の機能を実験的に評価するには,その反応を同定して平衡定数等のパラメータを決定することが実験の現場で必要になることが多い。また,蛋白質の挙動をモデル化して理解したり予測したりするには,平衡論で反応スキームを描くことがしばしば必要である。しかし,記号と矢印で反応スキームを描くのは出発点に過ぎない。実験データと照らし合わしてその反応スキームの妥当性を検討し,さらには解析を行って平衡定数等の算出をすることで,議論や応用の対象になるのである。そのような解析においては,反応スキームがどのように実験的に測定されるかを記述するモデル関数を導出することが重要なステップである。
吸光測定や蛍光測定は,蛋白質のリガンド結合やコンフォメーション変化の平衡反応の測定によく使われる方法である。これは,トリプトファン,補欠分子族,そして蛋白質に結合させた色素の吸光や蛍光の特性が,蛋白質のコンフォメーションやリガンド結合を反映するためである。また,近年,様々な標的分子を検出する蛍光蛋白質センサープローブも開発され,試験管内や生体内の実験で広く使われている[1]。このように測定手法が多様化することで,様々な分子が測定対象となった。そこで,以下では,測定された吸光度や蛍光強度データを適切に取り扱うための解析の基本原理について述べる。蛋白質の平衡反応の測定データはしばしば最小自乗フィッティングで解析され,リガンドの結合定数やコンフォメーション間の平衡定数といった解析値が算出される。最小自乗フィッティングによる解析の要となるのは,解析のためのモデル関数を導出することである。実験データを解析するための多くのモデル関数には,
- リガンド濃度等の独立変数に対する,各蛋白質分子種のモル分率の応答を与える項
- 各蛋白質分子種のモル分率を関数とする,測定強度の理論値を与える項
が含まれる[2]。研究室によっては,そのようなモデル関数をどのように立てるのかといった基本原理について指導を行っているところもあるかもしれないし,あるいはあまりに明らか過ぎるために具体的な解説や指導もなく,先輩の院生やスタッフから言われるままに解析手順を学生が踏襲しているところもあるだろう。筆者自身は逆の立場で,これまでに学生に吸光や蛍光測定データを使った蛋白質平衡反応解析の方法を指導する機会が時々あった。そのような指導を繰り返すうちに,指導内容に加えてそれに関連する内容を合わせてまとめておきたいと思い立った次第である。そこで,本稿では,蛋白質の平衡反応の吸光度データや蛍光強度データを解析するための基本原理をあえて確認し,さらにいくつかの例題を示しながら解析の方法について解説することにした。
2. データ解析に用いるモデル関数を導出するための基礎事項
本稿を通して,測定下の蛋白質 \(\mathrm{M}\) が,
\[ \ce{M_{0} <=> M_{1} <=> \dotsm <=> M_{\mathit{N}}} \tag{2.1} \]
といういくつかのコンフォメーションや化学状態の平衡にあるときに,測定される吸光度あるいは蛍光強度(以降,両者を区別しないときは単に「強度」と総称することにする)を記述するモデル関数を立てることを目標とする。この平衡反応は,コンフォメーション間の平衡と考えても良いし,あるいはリガンドの結合と考えても良く,本稿ではいずれも取り上げる。反応 (2.1) を吸光測定や蛍光測定で解析する過程で本稿が使う基礎事項は以下の2つである。
2.1. 測定強度の線形性(斉次性と加法性)
反応 (2.1) の平衡状態にある蛋白質を吸光測定や蛍光測定で解析することを想定する。蛋白質のある分子種 \(\ce{M_{\mathit{k}}} \ (k = 0, 1, \dots , N)\) のモル分率が 100% の時の強度を \(A_{k}\) としたとき,平衡状態において測定される強度 \(A\) のモデル関数を
\[ A_{\textrm{model}} = \alpha_{0}A_{0} + \alpha_{1}A_{1} \dots + \alpha_{N}A_{N} \tag{2.2} \]
という線形結合で記述する[2]。ここで,\(\alpha_{k}\) は,測定下の蛋白質分子種 \(\textrm{M}_{k}\) のモル分率
\[ \alpha_{k} = \frac{[\mathrm{M}_{k}]}{\displaystyle \sum^{N}_{k = 0}[\mathrm{M}_{k}]} \tag{2.3} \]
である。式 (2.2) では,測定強度値における \(\mathrm{M}_{k}\) の寄与分が \(\alpha_{k} \cdot A_{k}\) であること(すなわち,強度は \(\mathrm{M}_{k}\) の濃度に比例すること,つまり斉次性),そして \(\mathrm{M}_{0}, \mathrm{M}_{1} \dots\) の強度寄与分の加法性が成り立つことを前提としている。
測定強度のモデル関数において式 (2.2) のような線形結合を許す根拠は何か?吸光度については,その発色団濃度に対する比例を示した Beer–Lambert の法則[3]である。また,蛍光強度については名前の付いた法則はないが,測定対象に含まれる蛍光源である発色団の濃度が増えると,それに比例して検出器に到達する蛍光由来の光子数は増加すると考えられる。さらに,吸光測定や蛍光測定に限らず,以上のような線形性を適用できる測定データ対しては,式 (2.2) の形のモデル関数を使うことが可能である。ただし,上記の法則が前提となるため,線形性が適用できる条件(十分希薄な濃度であるか等)において実験することも心がけなければならない。
2.2. 質量作用の法則
質量作用の法則(mass action law)は,
\[ \ce{\mathit{p}_{1}A_{1} + \mathit{p}_{2}A_{2} + \dotsm <=> \mathit{q}_{1}B_{1} + \mathit{q}_{2}B_{2} + \dotsm} \tag{2.4} \]
という平衡反応における反応商(reaction quotient)
\[ K_{\mathrm{eq}} = \frac{[\mathrm{B}_{1}]^{q1}[\mathrm{B}_{2}]^{q2} \dots}{[\mathrm{A}_{1}]^{p1}[\mathrm{A}_{2}]^{p2} \dots} \tag{2.5} \]
の \(K_{\mathrm{eq}}\) が一定であるとするものである。ここでの \(K_{\mathrm{eq}}\) を平衡定数という。\(K_{\mathrm{eq}}\) は反応に含まれる分子種の濃度に依存しないが,温度に依存する。なお,本稿では,活量係数については平衡定数の中に繰り込まれていると考えることで,明示的に取り扱わないことにする。
3. 1個のリガンド結合部位をもつ蛋白質の解析
蛋白質 \(\ce{M}\) とリガンド \(\ce{X}\) の結合反応
\[ \ce{M + X <=>[$K$] MX} \tag{3.1} \]
の吸光あるいは蛍光スペクトルデータの解析を行うことにする。本節では簡単のために,リガンドの結合部位が1個ということを既知とする。本稿で取り扱う解析手順は以下の通りである:
- \(\ce{X}\) の濃度の関数として測定強度を測定する滴定実験を行う。\(\ce{X}\) の濃度変化によって蛋白質分子種 \(\ce{M}\), \(\ce{MX}\) の濃度が変化するので,それに伴って測定強度が変化する。
- 最小自乗法でモデル関数を測定強度データにフィットさせて,結合定数K 等のパラメータを算出する。モデル関数は,\(\ce{M}\), \(\ce{MX}\) の濃度またはモル分率を含む形となる。
通常の実験では,吸光分光光度計や蛍光分光光度計で測定される測定強度の誤差が示す分布は概ね正規分布に近い。したがって,反応に関わるパラメータ値を推定するための回帰分析手法としては,モデル関数と測定値との差分の自乗和の最小化によって最尤推定を行う最小自乗法が相応しい。
3.1. 1波長測定による解析
3.1.1. 解析のためのモデル関数
本節では,反応 (3.1) において測定される測定強度のモデル関数を導出する。反応 (3.1) における平衡定数は,質量作用の法則より
\[ K = \frac{[\mathrm{MX}]}{[\mathrm{M}][\mathrm{X}]} = \frac{[\mathrm{MX}]}{[\mathrm{M}]x} \tag{3.2} \]
である。ここで,\(x\) は遊離しているリガンドの濃度である。式 (3.2) の平衡定数 \(K\) は,(反応式 (3.1) を,リガンド結合する方向にとっていることより)特に結合定数と呼ばれるものであり,(リガンド結合部位が1個の場合の)次元は濃度の逆数である。リガンド結合部位が1個の場合は濃度と同じ次元をもつ解離定数(\(= 1/K\))もよく使われるが,結合部位が2個以上の場合や,2種類以上のリガンドを含む系では,結合定数を用いた方が式中に現れる分数の個数を少なくできるという数式展開の点で都合が良い。結合定数 (3.2) を用いれば,\(\mathrm{M}\), \(\mathrm{MX}\) のモル分率 \(\alpha_{\mathrm{M}}\), \(\alpha_{\mathrm{MX}}\) は,
\[ \alpha_{\mathrm{M}} = \frac{[\mathrm{M}]}{[\mathrm{M}] + [\mathrm{MX}]} = \frac{1}{1 + K_{x}} \tag{3.3} \]
\[ \alpha_{\mathrm{MX}} = \frac{[\mathrm{MX}]}{[\mathrm{M}] + [\mathrm{MX}]} = \frac{1}{1 + K_{x}} \tag{3.4} \]
となる。分子種 \(\mathrm{M}\), \(\mathrm{MX}\) のモル分率が 100% の時の強度をそれぞれ \(A_{\mathrm{M}}\), \(A_{\mathrm{MX}}\) として式 (3.3),(3.4) を式 (2.2) に適用すれば,
\[ A(x) = \alpha_{\mathrm{M}}A_{\mathrm{M}} + \alpha_{\mathrm{MX}}A_{\mathrm{MX}} = \frac{1}{1 + Kx} A_{\mathrm{M}} + \frac{Kx}{1 + Kx} A_{\mathrm{MX}} \tag{3.5} \]
が得られる。これが,反応 (3.1) の測定強度についてのモデル関数である。
図1に式 (3.5) のモデル関数を適用した解析例を示す。図1Aのスペクトルの波長 \(\lambda_{1}\) から吸光度をとり,リガンド濃度に対してプロットしたのが図1Bである。このプロットに対して,式 (3.5) のモデル関数の最小自乗フィッティングを行った結果得られた曲線が図1Bの実線になる。これにより,結合定数 \(K\) の値に加えて,\(\mathrm{M}\) または \(\mathrm{MX}\) のモル分率が 100% の時の吸光度 \(A_{\mathrm{M}}\) または \(A_{\mathrm{MX}}\) を算出することができる。ソフトウェアを用いた具体的な解析手順については,第5節を参照して頂きたい。
ここで一つ注意点を指摘しておくが,1波長の強度データの式 (3.5) による解析では,強度をとる波長は固定である。滴定実験中は,リガンド濃度の変化に伴ってピーク波長がシフトしていくかもしれないが,それに気をとられずに固定した波長から強度を取るべきである。なぜならば,式 (3.5) のモデル関数に含まれているパラメータ \(A_{\mathrm{M}}\) と \(A_{\mathrm{MX}}\) が定数という前提が含まれているからである。リガンド濃度変化に伴って,強度をモニターする波長を変えることは,この前提を破ることを意味する。
3.1.2. スペクトルからのモル分率の直読
反応 (3.1) のように蛋白質分子種が \(\mathrm{M}\), \(\mathrm{MX}\) の2種の場合には,それらのモル分率をスペクトルから直接読み取ることもしばしば行われている。実際,測定データの前処理法として,先輩の院生やスタッフからそのように習うという研究室も多いことであろう。図1Cに強度値の取り方を示す。この方法では,\(x = 0\) 時の強度を \(A_{1}\),\(x\) が十分高いときの強度を \(A_{2}\),そして任意のリガンド濃度 \(x\) のときの強度を \(A_{x}\) ととり,
\[ \frac{[\mathrm{M}]}{[\mathrm{M}] + [\mathrm{MX}]} = \frac{A_{2} - A_{x}}{A_{2} - A_{1}}, \mspace{10mm} \frac{[\mathrm{MX}]}{[\mathrm{M}] + [\mathrm{MX}]} = \frac{A_{x} - A_{1}}{A_{2} - A_{1}} \tag{3.6} \]
によって \(\mathrm{M}\) と \(\mathrm{MX}\) のモル分率を計算する[2]。実は,式 (3.5) を変形することによって,式 (3.6) と同様の形の式が得られる。
ここでは,\(A_{1}\), \(A_{2}\) がそれぞれ \(A_{\mathrm{M}}\), \(A_{\mathrm{MX}}\) に対する良い近似となっているか?ということ,そして,\(A_{1}\), \(A_{2}\) に測定誤差がどれだけ含まれているか?に注意する必要がある。実際,この方法では,\(A_{1}\), \(A_{2}\) の値が正確に決まったという前提に立ってモル分率を計算しているが,現実の実験では測定装置のノイズやドリフトもあればピペッティングの誤差もある。また,場合によっては,\(\mathrm{M}\) 型がモル分率 100% の強度および \(\mathrm{MX}\) 型 100% を実験的に測定できない場合もある(たとえば,pH 滴定では \(\ce{H+}\) 濃度がゼロや無限大になる前に蛋白質が変性するかもしれないし,あるいは解析対象外の別のコンフォメーションに変化するかもしれない)。以上のような点で問題なければ,式 (3.6) を使っても良いであろう。一方,式 (3.5) のモデル関数を用いた場合は,\(A_{\mathrm{M}}\), \(A_{\mathrm{MX}}\) の強度値もフィッティングで算出するので,ここで指摘したような気遣いの必要が減るという点で都合が良い。
さらに,スペクトルデータからモル分率を直接読み取った後,モル分率とリガンド濃度のデータを変換して線形プロットに載せるという手法も従来は広く行われてきた。たとえば,両逆数プロットは典型例である。モル分率の逆数をリガンド濃度の逆数に対してプロットする両逆数プロットに対応する関数を求めるために,式 (3.4) の両辺の逆数を取れば,
\[ \frac{1}{\alpha_{\mathrm{MX}}} = 1 + \frac{1}{K} \cdot \frac{1}{x} \tag{3.7} \]
であるので,両逆数プロットの傾きの逆数が結合定数となる。滴定実験のデータで線形プロットを用いる方法は,PC があまり普及していなかった時代にはよく使われた。しかし,昨今では一人一台で PC を使うことが普通になるとともに,グラフソフトウェア上の非線形フィッティングも手軽にできるようになったので,それらのプロット法はそれほど有用ではなくなった。もちろん,両逆数プロットを用いて1次関数で最小自乗フィッティングを行っても良いが,逆数をとることで各データポイントに含まれる測定誤差に偏りが発生することは覚えておく必要がある。その際には測定データの誤差もワークシートに入力し,各データポイントの測定誤差も含めて最小自乗フィッティングを行うと良いだろう。
3.1.3. リガンド濃度の取り扱い:遊離リガンド濃度,総リガンド濃度の選択
以上の計算で用いたリガンド \(\ce{X}\) の濃度 \(x\) は,あくまでも,反応 (3.1) におけるリガンドの分子種 \(\ce{X}\) の濃度である。つまり,\(x\) は,\([\ce{X}] + [\ce{MX}]\) ではなく,\([\ce{X}]\) なのである。同じことだが念を押せば,\(x\) は蛋白質に結合していない遊離したリガンド \(\ce{X}\) の濃度である。これは,\(\ce{H+}\) をリガンドとして pH メータで \(\ce{H+}\) を測定するときや,その他,酸素電極やイオン電極でリガンド濃度を測定するときは,測定器が表示する値をそのまま \(x\) としても良いだろう。また,pH 緩衝溶液や \(\ce{Ca^{2+}}\) 緩衝溶液のようにバッファーでリガンド濃度を固定するときも所定の濃度を \(x\) として良いだろう。しかし,いくつかの場合では,リガンド濃度の取り扱いには工夫が必要である。以下では,実験で遭遇しそうないくつかのケースについて説明する。ここで,測定溶液中に加えた総蛋白質濃度を \(\ce{[M]_{T}}\), 総リガンド濃度を \(\ce{[X]_{T}}\) と書くことにする:
\[ \ce{[M]_{T}} = \ce{[M]} + \ce{[MX]} \tag{3.8} \]
\[ \ce{[X]_{T}} = \ce{[X]} + \ce{[MX]} = x + \ce{[MX]} \tag{3.9} \]
【ケース1】\(1/K \gg \ce{[M]_{T}}\) の場合
\(\alpha_{\ce{MX}} = 1/2\) となるリガンド濃度 \(x\) が \(1/K\) であるので,滴定実験で用いる\(\ce{[X]_{T}}\) の範囲は \(1/K\) の前後付近をとるのが通常である(たとえば,\(0.1/K\) – \(10/K\) くらいの範囲)。つまり,このケースでは,実験で用いるリガンド総濃度 \(\ce{[X]_{T}}\) は,蛋白質総濃度 \(\ce{[M]_{T}}\) にくらべて十分に過剰である。したがって,良い近似で \(\ce{[X]_{T}} \approx x\) と見なして滴定曲線をとっても良い。
【ケース2】リガンド \(\ce{X}\) をバッファーで与える場合
pH 緩衝溶液や \(\ce{Ca^{2+}}\) 緩衝溶液等の緩衝溶液を使うことで遊離リガンド濃度 \(x\) をコントロールすれば,蛋白質との結合反応が起こっても遊離リガンド濃度の変動を低減することができる。このときも,バッファーを調製したときのリガンド濃度を \(x\) として滴定曲線を描いても良い。ただし,十分な濃度の緩衝剤を加えることにより,反応 (3.1) が起こっても遊離リガンド濃度 \(x\) の変動が解析上問題ない程度に小さいことを実験プロトコル上確認しておく必要があるだろう。試料溶液中のバッファー濃度が十分かどうかに気を遣うのは,蛋白質実験の常識・基本の一つである。
【ケース3】\(1/K \sim \ce{[M]_{T}}\),あるいは \(1/K < \ce{[M]_{T}}\) の場合
これは,リガンドの蛋白質に対する結合の親和性が高いケースである。この条件における滴定実験では,用いる遊離リガンド濃度 \(x\) や総リガンド濃度 \(\ce{[X]_{T}}\) を \(\ce{[M]_{T}}\) の前後やそれ以下にとることが必要であること,そして,試料溶液に加えた総リガンド量のうち,かなりの割合が蛋白質に結合するために \(x \approx \ce{[X]_{T}}\) という近似が使えない条件で測定になることに注意する。こういう注意点を看過してケース1と同様な \(x \approx \ce{[X]_{T}}\) という近似が可能だと勘違いをして式 (3.5) で解析をすると,解析結果にかなりの誤差を招いてしまう。
例題として,リガンドの蛋白質に対する結合の親和性が非常に高い状況(\(1/K \ll \ce{[M]_{T}}\))を思考実験することにしよう。この場合,リガンド \(\ce{X}\) の添加によって反応 \(\ce{M + X -> MX}\) が一方的に進む。滴定実験において \(\ce{X}\) の濃度を徐々に増やしながら \(\ce{[M]}\) と \(\ce{[MX]}\) を測定すると,\(\ce{[X]_{T}}\) が低いときは分子種 \(\ce{M}\) が支配的,\(\ce{[X]_{T}} = \ce{[M]_{T}}/2\) の時に \(\ce{[M]} = \ce{[MX]}\),そして \(\ce{[X]_{T}}\) をさらに増やしていくと分子種 \(\ce{MX}\) が支配的になって飽和する,という結果になる。こういう場合でも,測定強度を \(\ce{[X]_{T}}\) に対してプロットすると,いかにもモデル関数 (3.5) が適用できそうな形状のグラフが得られてしまう。ただし,このような滴定データにモデル関数 (3.5) を適用して解析すると,結合定数の解析値は \(K = 2/\ce{[M]_{T}}\) 前後となるであろう(つまり,こうして得られた \(K\) の解析値は,総蛋白質濃度 \(\ce{[M]_{T}}\) に依存する)。しかし,そのような解析値は結合定数の真の値を反映するものではない。特に親和性が高い場合の滴定実験では,非常に低い濃度のリガンドおよび蛋白質で,慎重を期したタフな滴定実験を行う必要があるが,ここで説明したようなことを忘れていると,頑張ってやったはずの滴定実験が単に \(2/\ce{[M]_{T}}\) といった蛋白質濃度を測っただけだったという残念な結果になりかねない。
このような問題点を解決する方法としては,以下が挙げられる:
- リガンドが低分子であれば,平衡透析を行い,透析内液で \(\mathrm{[M]}\),\(\mathrm{[MX]}\) を測定し,透析外液中のリガンド濃度を測定して \(x\) 値とする
- 蛋白質総濃度 \(\mathrm{[M]_{T}}\) に比べて,\(1/K\) 値がそれほど低くなければ,式 (3.5) のモデル関数の独立変数を \(\mathrm{[X]_{T}}\) とする変形を行うこともできる(下記参照)。
後者の場合,\(K\), \(\mathrm{[X]_{T}}\), \(\mathrm{[M]_{T}}\) から遊離リガンド濃度 \(x\) を与える関数と式 (3.5) を併せて使って最小自乗フィッティングを行っても良いだろう。すなわち,式 (3.2),(3.8),(3.9) より得られる解
\[ x = \frac{-\{1 + K(\mathrm{[M]_{T}} - \mathrm{[X]_{T}})\} + \sqrt{\{1 + K(\mathrm{[M]_{T}} - K\mathrm{[X]_{T}})\}^{2} + 4K\mathrm{[X]_{T}}}}{2K} \tag{3.10} \]
を式 (3.5) に代入すれば,\(\mathrm{[M]_{T}}\), \(\mathrm{[X]_{T}}\) を独立変数としたモデル関数を導出できる。
3.2. 2波長測定による解析(強度比による Ratiometry 解析)
2波長の強度比をとる測定は,蛋白質の濃度の変動や誤差をキャンセルできるという点で有用であり,分光光度計によるキュベット中での測定のみならず,蛍光顕微鏡観察でもしばしば使われている。Ratiometry 解析する際は,データの前処理や強度比をとる波長の選択で注意が必要である。本節ではこれら2点について説明する。
データの前処理で必要なことは,測定強度に含まれるバックグラウンドやオフセット値を差し引いて,蛋白質由来の正味の強度値を算出しておくことである。この前処理が必要な理由は,2.1節で説明した測定強度の線形性を確保することで,実測された強度比をモデル関数で適切に解析するためである。蛍光強度の場合は,試料やガラス等が由来の自家蛍光,測定装置内外からの迷光,そして光検出器の暗電流などがそのバックグラウンドの原因である。吸光度では,不純物や試料溶液の濁度などがバックグラウンドになる。また,顕微鏡観察で用いる EMCCD,sCMOS 等のカメラでは,暗電流に加えて,読み出される輝度にオフセットを一律に加算しているものもある。以上のように,生の測定値からバックグラウンド値やオフセット値を差し引いた後に強度比を計算し,さらに解析を行うのが正しい手順である。
次に,強度比を得るための2つの波長に選択について説明する。確かに,2つの波長の選択に際して注意を払わずに強度比をとったとしても,強度比のリガンド濃度 \(x\) の依存性はしばしば式 (3.5) と同様な曲線となる。しかし,強度比のプロットの解析において式 (3.5) のモデル関数をそのまま使ってフィッティングを行うと,算出される \(K\) の解析値は真の値からシステマティックにずれることがある。どこに問題があるのかを知るために,リガンド濃度 \(x\) に対する強度比のモデル関数を導出してみよう。図1Aにあるように,波長 \(\lambda_{1}\) の吸光度に加えて,波長 \(\lambda_{2}\) における吸光度をとり \(B(x)\) とする。\(\ce{M}\),\(\ce{MX}\) のモル分率が 100% の時の \(B\) の強度値をそれぞれ \(B_{\mathrm{M}}\), \(B_{\mathrm{MX}}\) とすると,式 (3.5) に相当する \(B\) のモデル関数は
\[ B(x) = B_{\mathrm{M}} \frac{1}{1 + Kx} + B_{\mathrm{MX}} \frac{Kx}{1 + Kx} \tag{3.11} \]
である。そこで,図1Dのように \(A/B\) 比をとると,
\[
\begin{align}
\frac{A(x)}{B(x)}
&=
\cfrac
{A_{\mathrm{M}} \cfrac{1}{1 + Kx} + A_{\mathrm{MX}} \cfrac{Kx}{1 + Kx}}
{B_{\mathrm{M}} \cfrac{1}{1 + Kx} + B_{\mathrm{MX}} \cfrac{Kx}{1 + Kx}}\
&=
\cfrac{A_{\mathrm{M}}}{B_{\mathrm{M}}} \cdot
\cfrac{1}{1 + \left( \cfrac{B_{\mathrm{MX}}}{B_{\mathrm{M}}} K \right) x} +
\cfrac{A_{\mathrm{MX}}}{B_{\mathrm{MX}}} \cdot
\cfrac{\left( \cfrac{B_{\mathrm{MX}}}{B_{\mathrm{M}}} K \right) x}{1 + \left( \cfrac{B_{\mathrm{MX}}}{B_{\mathrm{M}}} K \right) x}
\tag{3.12}
\end{align}
\]
を得る。よく見てみれば,これは,式 (3.5) と同様の形をしているが,結合定数に相当する項が異なる(分母同士を比較すれば分かる)。すなわち,式 (3.5) から (3.12) へ移行するにあたり,
\[ K \to \frac{B_{\mathrm{MX}}}{B_{\mathrm{M}}} K \tag{3.13} \]
という変換が(不本意にも)施されている。このことは,\(A(x)/B(x)\) をリガンド濃度 \(x\) に対してプロットしたデータに対して式 (3.5) のモデル関数で最小自乗フィッティングを行った場合,そこで得られる \(K\) 値は,真の結合定数値の \(B_{\mathrm{MX}}/B_{\mathrm{M}}\) 倍として算出されるということを意味する。図1Dに強度比のプロットを示すが,\(A/B\) 比の低濃度極限と高濃度極限の中間値となるリガンド濃度が,図1Bと一致していないことが分かるであろう。
このようなアーティファクトを避ける方法の一つとして,図1Aの \(\lambda_{\mathrm{iso}}\) のような等吸収点(isosbestic point)あるいは等発光点(isoemissive point; isolampsic point)を強度 \(B\) の波長にとることがあげられる。なぜなら,等吸収点や等発光点を \(B\) 値とすれば \(B_{\mathrm{M}} = B_{\mathrm{MX}}\) なので,式 (3.13) において \(K\) 値のシフトが発生しないからである。あるいは,強度比の補正を施した式 (3.12) で解析をすることでもアーティファクトを避けることができる。
3.3. リガンド結合に伴うアロステリック効果
以上の各節では,反応 (3.1) の蛋白質分子種 \(\ce{M}\) および \(\ce{MX}\) と,測定される強度 \(A_{\mathrm{X}}\),\(A_{\mathrm{MX}}\) が 1:1 に対応すると暗黙のうちに仮定してモデル関数の導出を行ってきた。たとえば,ミオグロビンの酸素平衡における吸光スペクトルは,酸素分子の結合解離と直接連動していると考えてもよいであろう。しかし,リガンド結合と測定強度との対応が間接的な場合もあるかもしれない。そこで本節では,測定強度の変化が,リガンド結合の直接的な効果ではなく,リガンド結合で誘起された蛋白質のコンフォメーション変化を反映したアロステリック効果[4]を含む場合について言及する。最も簡単なケースは以下のスキームであろう:
\[
\begin{array}{ccc}
\mathrm{M_{0}} & \to & \mathrm{M_{1}} \
\downarrow & & \downarrow \
\mathrm{M_{0}X} & \to & \mathrm{M_{1}X}
\end{array}
\tag{3.14}
\]
ここで,コンフォメーション0(\(\mathrm{M_{0}}\) と \(\mathrm{M_{0}X}\))はリガンド結合にかかわらず同じスペクトルを示し,コンフォメーション1(\(\mathrm{M_{1}}\) と \(\mathrm{M_{1}X}\))もリガンド結合にかかわらず同じスペクトルを示すが,コンフォメーション0と1ではスペクトルが異なると仮定する。この反応の諸定数は
\[
\begin{align}
^{0}K &= \frac{[\mathrm{M_{0}X}]}{[\mathrm{M_{0}}]x},
\mspace{10mm}
^{1}K = \frac{[\mathrm{M_{1}X}]}{[\mathrm{M_{1}}]x},
\tag{3.15}
\
L_{10} &= \frac{[\mathrm{M_{1}}]}{[\mathrm{M_{0}}]}
\tag{3.16}
\end{align}
\]
とする。以上を再編成した関係式
\[ \frac{\mathrm{M_{0}X}}{\mathrm{M_{0}}} = \, ^{0}Kx, \mspace{10mm} \frac{\mathrm{M_{1}X}}{\mathrm{M_{0}}} = L_{10} \, ^{1}Kx, \tag{3.17} \]
より,コンフォメーション0および1のモル分率 \(^{0}\alpha\),\(^{1}\alpha\) は,
\[
\begin{align}
^{0}\alpha
&= \frac
{[\mathrm{M_{0}}] + [\mathrm{M_{0}X}]}
{[\mathrm{M_{0}}] + [\mathrm{M_{0}X}] + [\mathrm{M_{1}}] + [\mathrm{M_{1}X}]}\
&= \frac
{1 + \, ^{0}Kx}
{1 + L_{10} + (^{0}K + L_{10} \, ^{1}K)x}
\tag{3.18}
\
^{1}\alpha
&= \frac
{[\mathrm{M_{1}}] + [\mathrm{M_{1}X}]}
{[\mathrm{M_{0}}] + [\mathrm{M_{0}X}] + [\mathrm{M_{1}}] + [\mathrm{M_{1}X}]}\
&= \frac
{L_{10} + L_{10} \, ^{1}Kx}
{1 + L_{10} + (^{0}K + L_{10} \, ^{1}K)x}
\tag{3.19}
\end{align}
\]
となるので,これらを式 (2.2) に適用することで以下のモデル関数を得ることができる:
\[ A(x) = \, ^{0}A \frac{1 + \, ^{0}Kx}{1 + L_{10} + (^{0}K + L_{10} \, ^{1}K)x} + \, ^{1}A \frac{L_{10} + L_{10} \, ^{1}Kx}{1 + L_{10} + (^{0}K + L_{10} \, ^{1}K)x} \tag{3.20} \]
ここで,\(^{0}A\),\(^{1}A\) は,それぞれコンフォメーション0,1のモル分率が 100% としたときの測定強度である。さらに,第1項,第2項の分数の分母を,\(1 + Kx\) の形に変形してまとめると,
\[
\begin{multline}
A(x) =
\frac{1}{1 + L_{10}} \times \
\shoveleft{
\left\{
(^{0}A + \, ^{1}AL_{10})
\cfrac{1}{1+ \cfrac{^{0}K + L_{10} \, ^{1}K}{1 + L_{10}}x} +
\cfrac{(1 + L_{10})(^{0}A^{0}K + ^{1}AL_{10} \, ^{1}K)}{^{0}K + L_{10} \, ^{1}K}
\cfrac{\cfrac{^{0}K + L_{10} \, ^{1}K}{1 + L_{10}}x}{1 + \cfrac{^{0}K + L_{10} \, ^{1}K}{1 + L_{10}}x}
\right\}
}
\tag{3.21}
\end{multline}
\]
と,式 (3.5) と同様な形に変形することができる。したがって,滴定曲線の形状のみから,スペクトル変化の原因がリガンド結合の直接的な効果なのか,あるいはリガンド結合に伴うアロステリック効果なのかは区別できない。また,式 (3.5) のモデル関数の形状が \(A_{\mathrm{M}}\),\(A_{\mathrm{MX}}\),\(K\) の3個のパラメータで規定されていることを考慮すれば,滴定曲線に対する式 (3.21) の最小自乗フィッティングだけで \(L_{10}\), \(^{0}K\),\(^{1}K\),\(^{0}A\),\(^{1}A\) をすべて一意に決定できない。それら5個のパラメータ値を決めるには,そのうち2個以上は別の実験で決めておく必要がある。また,このケースでは協同性はあらわれず,Hill 係数は1となる。
4. 1種類のリガンドで2個以上の結合部位をもつ蛋白質の解析
本節では,1種類のリガンドの結合部位が2個以上で,蛋白質がいくつかのコンフォメーションをとり,アロステリック効果を含む場合を説明する。この場合の一般的な反応スキームは,文献[4]に倣えば,以下のように書ける:
\[
\begin{array}{ccccccc}
\mathrm{M_{0}} & \to & \mathrm{M_{1}} & \to & \dotsm & \to & \mathrm{M}_{t}\
\downarrow & & \downarrow & & & & \downarrow\
\mathrm{M_{0}X} & \to & \mathrm{M_{1}X} & \to & \dotsm & \to & \mathrm{M}_{t}\mathrm{X}\
\downarrow & & \downarrow & & & & \downarrow\
\vdots & & \vdots & & & & \vdots\
\downarrow & & \downarrow & & & & \downarrow\
\mathrm{M}_{0}\mathrm{X}_{N} & \to & \mathrm{M}_{1}\mathrm{X}_{N} & \to & \dotsm & \to & \mathrm{M}_{t}\mathrm{X}_{N}
\end{array}
\tag{4.1}
\]
結合段階数 \(N\) や取り得るコンフォメーション数 \(t\) が多い場合や未知の場合は特に,このスキームにおける全ての平衡定数を実験的に決めることは困難であるため,より簡単化されたモデルがよく用いられる。ここでは,簡単化されたモデルとして,逐次結合反応と協同性反応について説明する。なお,多重平衡反応理論の詳細は本稿の範囲をはるかに超えるので,文献[2][4][5]を参照して頂きたい。
4.1. 逐次結合反応(Adair の式の応用)
簡単化の一つは,反応 (4.1) における結合リガンド数が同じ蛋白質分子種のコンフォメーションを1種類とするものである。すなわち,反応 (4.1) の1つの列だけが許されると考えるものである。たとえば,horse heart cytochrome c の pH 滴定[6]などはこのタイプに相当するであろう。この場合,リガンド結合の逐次反応
\[ \ce{M -> MX -> MX2 \dotsm -> MX_{\mathit{N}}} \tag{4.2} \]
を考えることになる。これについてモデル関数を導出する。まず,反応
\[ \ce{M + jX <=> MX_{j}} \tag{4.3} \]
に注目し,その結合定数 \(K_{j}\) を,
\[ K_{j} = \frac{[\mathrm{MX}_{j}]}{[\mathrm{M}]x^{j}} \tag{4.4} \]
とする。ここから,\(j\) 個のリガンドが結合した蛋白質分子種 \(\ce{MX_{j}}\) のモル分率を求める。式 (4.4) より \([\mathrm{MX}_{j}] = [M]K_{j}x^{j}\) なので,すべてのリガンド結合蛋白質分子種の濃度和は,
\[ \sum_{j}[\mathrm{MX}_{j}] = [M] \{1 + K_{1}x + K_{2}x^{2} + \dots + K_{N}x^{N} \} \tag{4.5} \]
と書ける。ここで,カギ括弧の中
\[ P = 1 + K_{1}x + K_{2}x^{2} + \dots + K_{N}x^{N} \tag{4.6} \]
は,結合多項式(binding polynomial)と呼ばれている[4][5]。これより,\(\mathrm{MX}_{j}\) のモル分率を \(\chi_{j}\) とすると,
\[ \chi_{j} = \frac{[\mathrm{MX}_{j}]}{\displaystyle \sum_{j}[\mathrm{MX}_{j}]} = \frac{K_{j}x^{j}}{1 + K_{1}x + K_{2}x^{2} + \dots + K_{N}x^{N}} = \frac{K_{j}x^{j}}{P} \tag{4.7} \]
が得られる。
測定強度のモデル関数を得るには,モル分率の式 (4.7) を式 (2.2) に適用すれば良い。そこで,蛋白質分子種 \(\ce{MX_{j}}\) がモル分率 100% の時の強度を \(A_{j}\) とすると,モデル関数として
\[ A_{\mathrm{model}}(x) = A_{0}\chi_{0} + A_{1}\chi_{1} + \dots + A_{N}\chi_{N} = \frac{1}{P} \left\{ A_{0} + A_{1}K_{1}x + \dots + A_{N}K_{N}x^{N} \right\} \tag{4.8} \]
を得る。歴史的にみると,これは Adair の式[7]の応用といえる。ここでは一般型を導出したが,現実問題としては,反応段階数は数段くらいが解析可能な範囲であろう。
4.2. 協同性反応(Hill の協同性の式の応用)
測定対象の蛋白質のリガンド結合部位が2個以上あるにもかかわらず,実験で得られた滴定曲線に変曲点が1個しか見あたらないとか,等吸収点や等発光点を持つというふうに2状態遷移に似たリガンド濃度依存性を示すことがある(たとえば,cytochrome c の pH 滴定[8][9]や,\(\ce{Ca^{2+}}\) センサー蛍光蛋白質[10])。そういう滴定実験のデータに対して,Hill の協同性の式[11]に倣ったモデル関数で解析することがしばしば行われている。これは,反応 (4.1) を
\[ \ce{M + nX <=> MN_{n}} \tag{4.9} \]
と近似し,蛋白質分子種としては \(\ce{M}\) と \(\ce{MX_{n}}\) の2つのみが存在するとみなしたモデル化である。ただし,\(n\) は整数に限らない。この場合,\(\ce{MX_{n}}\) のモル分率 \(\theta\) は,
\[ \theta = \frac{[\ce{MX_{n}}]}{[\ce{M}] + [\ce{MX_{n}}]} = \frac{(K_{\mathrm{H}}x)^{n}}{1 + (K_{\mathrm{H}}x)^{n}} \tag{4.10} \]
と書くことにする。これを式 (2.2) に適用して,
\[ A_{\mathrm{model}}(x) = D_{0}(1 - \theta) + D_{n}\theta = D_{0} \frac{1}{1 + (K_{\mathrm{H}}x)^{n}} + D_{n} \frac{(K_{\mathrm{H}}x)^{n}}{1 + (K_{\mathrm{H}}x)^{n}} \tag{4.11} \]
と,測定強度のモデル関数を得ることができる。このモデルを使った解析例を図4に示す(詳細は第5節を参照)。ここで,\(D_{0}\),\(D_{n}\) は,強度のリガンド低濃度極限と高濃度極限である。Hill プロットは,\(\theta / (1 - \theta)\) の対数を \(x\) の対数に対してプロットしたものであり,Hill プロットの傾きが Hill 係数である。この場合の Hill 係数は,もちろん,
\[ n_{\mathrm{H}} = \frac{\partial}{\partial \ln x} \left( \ln \frac{\theta}{1 - \theta} \right) = n \tag{4.12} \]
であるので,反応 (4.9) における \(n\) 値が Hill 係数となる。ただし,一般的にはリガンド濃度が低い領域および高い領域では,実際の滴定データの Hill プロットの傾きは1に近づくが[4],式 (4.10) のモデルにおける Hill プロットの傾きはリガンド濃度全域で \(n\) となる点では,実測値とモデル曲線には多少の差異が生じる。
実のところ,反応 (4.9) および式 (4.10) のモデルにおける Hill 係数の具体的な物理的意味はあまり明らかではない。実際,同じ蛋白質についてモデル化した反応 (4.9) の \(n\) と,反応 (4.2) の全段階数 \(N\) については,\(n \le N\) という制約は存在するが,\(n\) と \(N\) は必ずしも一致しない。ただし,具体的なメカニズムを盛り込めば,Hill 係数の物理的な意味を直感的に理解しやすくなることもある。以下でその一例を示す。
蛋白質が2つのコンフォメーションをとり,それらの間の平衡がリガンド \(\ce{X}\) によってシフトするというモデルを考える:
\[
\begin{array}{ccc}
\ce{M0} & \to & \ce{M1}\
\downarrow & & \downarrow\
\ce{M0X} & \to & \ce{M1X}\
\downarrow & & \downarrow\
\vdots & & \vdots\
\downarrow & & \downarrow\
\ce{M0X_{\mathit{N}}} & \to & \ce{M1X_{\mathit{N}}}
\end{array}
\tag{4.13}
\]
ここでの強度測定は,リガンド結合数は検出できないが,コンフォメーション0と1を区別して検出できるものとする。これは,3.3節のモデルを,多段階リガンド結合に拡張したものである。例えば,2個以上の水素イオン,2価の陽イオン,あるいは変性剤等の結合解離でコンフォメーション変化が起こり,その結果起こるスペクトル変化をモニターしている場合に相当する。そこで,リガンド結合数に依らずコンフォメーション1全体のモル分率を \(\theta\) ととることにする:
\[ \theta = \frac {\displaystyle \sum_{k}[\ce{M1X_{\mathit{k}}}]} {\displaystyle \sum_{j=0,1}\sum_{k}[\ce{M_{\mathit{j}}X_{\mathit{k}}}]}, \mspace{10mm} 1 - \theta = \frac {\displaystyle \sum_{k}[\ce{M0X_{\mathit{k}}}]} {\displaystyle \sum_{j=0,1}\sum_{k}[\ce{M_{\mathit{j}}X_{\mathit{k}}}]} \tag{4.14} \]
これらモル分率を使うと,Hill プロットの縦軸は
\[ \ln \frac{\theta}{1 - \theta} = \ln \frac {\displaystyle \sum_{k}[\ce{M1X_{\mathit{k}}}]} {\displaystyle \sum_{k}[\ce{M0X_{\mathit{k}}}]} \tag{4.15} \]
である。この右辺は
\[ K_{01} = \frac {\displaystyle \sum_{k}[\ce{M1X_{\mathit{k}}}]} {\displaystyle \sum_{k}[\ce{M0X_{\mathit{k}}}]} \tag{4.16} \]
の対数,すなわちコンフォメーション0,1間の平衡定数の対数になっている。よって,Hill プロットの傾きである Hill 係数は,
\[ n’_{H} = \frac{\partial \ln K_{01}}{\partial \ln x} \tag{4.17} \]
である。実は,平衡定数の対数 \(\ln K_{01}\) を \(\ln x\) に対してプロットしたものは,「Wyman プロット」と呼ばれるものに相当しており,そのプロットの曲線の微係数は遷移に伴うリガンド結合数の差分であることが知られている[4][5]:
\[ n’_{\mathrm{H}} = \frac{\partial \ln K_{01}}{\partial \ln x} = \bar{X}_{1}(x) - \bar{X}_{0}(x) = \Delta \bar{X}(x) \tag{4.18} \]
ここで,\(\bar{X}_{0}(x)\),\(\bar{X}_{1}(x)\) は,リガンド濃度が \(x\) である時のコンフォメーション0, 1のリガンド結合数(コンフォメーション0あるいは1をとる蛋白質1モルあたりに結合しているリガンドのモル数)である。すなわち,ここで議論したモデルにおいては,Hill 係数はコンフォメーション変化前後のリガンド結合数の差に相当する。式 (4.18) の導出と意味は,本稿末尾の補足で説明する。
5. 解析例
5.1. 1個のリガンド結合反応
本節では,1個のリガンド結合部位を持つ蛋白質の反応 (3.1) を解析した例題を示す。最初に結果を示し,次いでグラフ作成・データ解析ソフトウェアである ORIGIN で実際に最小自乗フィッティングを行ったスナップショットを参照しながら,具体的なフィッティングの手順を例示する。
5.1.1. 1 個のリガンド結合反応の解析結果
図1Aに示した吸光スペクトルデータは,例示の目的で筆者がコンピュータ上で作成したものである。分子種 \(\ce{M}\) と \(\ce{MX}\) の吸光スペクトル曲線と \(K = 1 \times 10^{5} \, \mathrm{M}^{−1}\) を与えて,式 (3.5) のモデル関数に誤差として乱数を加えて生成した。スペクトルから波長 \(\lambda_{1}\) における吸光度を抽出し,リガンド濃度 \(x\) に対してプロットしたのが図1Bである。この例題では反応メカニズムの答えを反応 (3.1) だと知っているので,解析には式 (3.5) を用いることにした。式 (3.5) を最小自乗法で図1Bのプロットに対してフィッティングした結果,実線の軌跡が得られ,結合定数の解析値は,\(0.997 \times 10^{5} \, \mathrm{M}^{−1}\) となった(これは乱数を加えたデータを使ったモンテカルロシミュレーションなので,もちろん,異なるデータセットを使う度に解析値に多少の変動がある)。
解析においては,図1Bでプロットすべき吸光度の波長について迷うかもしれない。ここでは,分子種 \(\ce{M}\) と \(\ce{MX}\) との吸光度差が大きいことを理由に波長 \(\lambda_{1}\) を選んだ。実際の測定データの解析においては,(1) 試料分子の分光学的性質に照らし合わして解析対象の現象を反映した強度変化が得られる波長,(2) リガンド,共溶媒,コンタミネーション等からの妨害がない波長,(3) 測定ノイズの少ない波長,そして (4) 強度変化の幅が大きい波長,などを指標にモニター波長を選ぶと良いであろう。
5.1.2. データ解析ソフトウェアを用いた実際の解析手順
この節では,筆者が使っているデータ解析・グラフ作成用ソフトウェアの ORIGIN(OriginLab, Northampton, MA, USA;Windows 版)を使った解析手順の概要を紹介する。非線形最小自乗フィッティングは,
- モデル関数の作成
- モデル関数のデータに対するフィッティング計算
の2つの手順から構成される。ORIGIN のスクリーンショットを参照しながら解析の流れを見ていくことにする。まず,ORIGIN を起動し,フィッティング対象のデータを表示しているグラフ窓をクリックしてアクティブ化して,メニューバーに「解析」を表示させる。さらに,メニューバーより「解析→フィット→非線形曲線フィット」を起動して(図2A),「NL Fit」窓を開く。
モデル関数の作成では,モデル関数のファイル名の指定,変数名の指定,そしてモデル関数の数式入力等を行う。「NL Fit」窓からユーザー定義関数の「フィット関数の新規作成」ボタンを押して「フィット関数ビルダー」窓を開く(図2B)。関数名を記入し,「変数とパラメータ」窓に入り,独立変数(リガンド濃度),従属変数(吸光度),そしてパラメータの変数名を指定する(図2C)。図2Cでは,式 (3.5) のパラメータ \(A_{\mathrm{M}}\),\(A_{\mathrm{MX}}\),\(K\) はこの窓内ではそれぞれ A_M,A_MX,K,従属変数を y,独立変数を x とした。設定を進めて,図2Dの「式形式の関数」窓では,「関数内容」欄に数式を記入する。さらに,必要があれば,それ以降の窓でパラメータの範囲等の諸条件も入力する。以上で,モデル関数の入力を完了する。
フィッティングは,モデル関数の選択,データの選択,パラメータの初期値設定,そしてフィッティング計算の順で行う。「NL Fit」窓から,カテゴリと関数を選択し(図3A),さらに解析対象のデータ選択が正しく行われているかを確認する。ORIGIN では,解析対象データをプロットしたグラフ窓をアクティブにしてからフィッティングを起動させると,それが解析対象データとして自動的に選択される(あるいは,「NL Fit」窓から解析対象のワークシート・カラムを設定してもよい)。次に,「Parameters」タブを選択し,パラメータの推測値(初期値)を設定する(図3B左)。最小自乗法のアルゴリズムとして広く使われている Levenberg-Marquardt 法では,予め設定されたパラメータの初期値を出発点として最適解を探す。最適解に近い推測値を設定してやると,異常解を避けて正常な最適解へ収束させやすい。式 (3.5) のモデル関数は,各パラメータの推測値をグラフ上から読み取りやすいように定式化している(図1E)。推測値を入力したら「\(\chi^{2}\)」ボタンを押し,入力したパラメータを初期値としたときのモデル曲線をグラフ上に描かせて確認する(図3B右)。モデル曲線がグラフ上に現れなかった場合,入力した数式に文法エラーがあったり,パラメータの初期値が最適値から遠かったりする可能性がある。さらに,フィッティングボタンを押すと,パラメータ値が収束条件に達するまで最適化計算を繰り返し,最終的に最適解を得る(図3C)。図3Dに表示したグラフによれば,モデル曲線はデータによく合ってようである。
最小自乗フィッティングは,ORIGIN の他にも,KaleidaGraph(Synergy Software, Reading, PA, USA)等のソフトウェアの非線形最小自乗フィッティングツールで式 (3.5) をユーザー定義関数として入力してやれば,行うことができる。これらのソフトウェアは,フィッティング計算に加えて計算結果をグラフ表示する機能が標準装備されているので便利である。その他にも,無料で配布されている gnuplot,C++ や FORTRAN で使用する数値計算ライブラリである IMSL(Rogue Wave Software, Louisville, CO, USA)や NAG Library(Numerical Algorithms Group, Oxford, UK),そして数学計算ソフトウェアの Mathematica(Wolfram Research, Champaign, IL, USA),MAPLE(Maplesoft, Waterloo, Canada),Matlab(MathWorks, Natick, MA, USA)等でもフィッティング計算が可能である。
5.2. シトクロム c の pH 滴定データ解析の実施例
本節では,筆者が実施した緑膿菌(Pseudomonas aeruginosa)のシトクロム c551(PA Cyt c)の pH 滴定実験[8]で得られたデータの解析例を説明する。この実験では,PA Cyt c の吸光スペクトルを pH 0.15–7.6 の範囲で測定することで,pH 変化に伴うコンフォメーションの変化をモニターした。その測定データに対して,モデル化と非線形最小自乗フィッティングを行うことで,水素イオンの PA Cyt c に対する結合定数や Hill 係数を求めた。
5.2.1. 生データからの定性的な情報の読み取り
フィッティング解析を始める前に,まずは実験データを眺めて,PA Cyt c のコンフォメーション変化について定性的な情報を読み取ることにする。図4AにPA Cyt c の吸光スペクトルの pH 変化を示す。また,図4Bには,代表的な波長として 532 nm の吸光度の pH に対するプロットを示す。これらのデータから以下のことに気づく:
- 図4Aより,低 pH 側および高 pH 側においてそれぞれ特異的な吸光スペクトルがあり、pH 変化に伴って吸光スペクトルがそれらへ漸近している(それぞれ,酸性型,中性型と呼ぶことにする)
- 図4Aにおいて,483, 509, 589, 648 nm に等吸収点がある
- 図4Bのプロットにおいて,酸性型と中性型との中点以外には,変曲点は見当たらないようだ
- 図4Bの吸光度変化の傾きから察するに,Hill 係数は1より大きいかもしれない
PA Cyt c が酸性および中性 pH で特異的な吸光スペクトルをもつことより,吸光スペクトルで類別される酸性型,中性型のコンフォメーションが存在していると解釈できる。また,等吸収点があることより,酸性型・中性型の2つのコンフォメーション間の遷移は,2状態遷移だと示唆される(すなわち,これら2状態間の遷移において,検出可能なモル分率を示す PA Cyt c の分子種は,酸性型および中性型の2種のみだと示唆される)。逆に,もしも吸光スペクトルが酸性型・中性型と異なる第3の吸光スペクトルを持つコンフォメーションが検出可能なモル分率で存在しているとすれば,等吸収点は存在しないであろう(より詳しくは,「(吸光スペクトルで類別される)酸性型・中性型間の遷移が2状態遷移かつそれらの吸光スペクトルに交わる点が存在するならば,等吸収点をもつ」は成り立つが,その逆の「等吸収点をもつならば,その遷移は2状態遷移である」は成り立つ場合もあれば成り立たない場合もある)。等吸収点に加えて,図4Bで酸性型・中性型の中点以外に変曲点が見られないことも,2状態遷移であることを支持している。
5.2.2. Hill の協同性モデルによる PA Cyt c のコンフォメーション遷移の解析
5.2.1節で読み取った情報をまとめれば,PA Cyt c は,特異的な吸光スペクトルを示す酸性型と中性型の2つのコンフォメーションをもち,これらのコンフォメーションのモル分率が pH に依存していると解釈された。また,酸型・中性型の間の遷移は,Hill 係数が1より大きい正の協同性が示唆された。以上より,Hill の協同性のモデルである式 (4.11) のモデル関数で,このコンフォメーション変化を記述できそうである。また,逆に,最小自乗フィッティング解析を行うことで,式 (4.11) のモデルが実験データを良く記述できるかどうかを確かめることができる。
図4Bの pH に対する吸光度のプロットに対して,式 (4.11) のモデル関数の最小自乗フィッティングを行った。ソフトウェアの操作手順は5.1.2節で説明したものと同様である。フィッティングによって,実測の吸光度のプロットによく合うモデル曲線を得ることができた(図4Bの実線)。これによって得られた最適解は,\(K_{\mathrm{H}} = 68.7 \, \mathrm{M}^{−1}\)(水素イオンの解離の pK に換算すると,1.83),\(n = 2.06\) と得られた。また,モデル曲線が実測値によく合っていることより,この解析で用いた Hill の協同性の2状態遷移モデルは,PA Cyt c の pH 依存性のコンフォメーション変化を良く記述しているようである。
5.2.3. Wyman プロットによる解析
さらに,4.2節で触れた Wyman プロットを PA Cyt c が中性型から酸性型へのコンフォメーション変化に適用した例を示す。Wyman プロットは,平衡定数の対数をリガンド濃度の対数に対してプロットしたものである。酸性型,中性型の分子種をそれぞれ \(\ce{M_{A}}\),\(\ce{M_{N}}\) と書くことにし,\(\mathrm{pH} = x\) における \(\ce{M_{A}}\) のモル分率を \(θ(x)\) とすると,
\[ \theta(x) = \frac{[\ce{M_{A}}]}{[\ce{M_{A}}] + [\ce{M_{N}}]}, \mspace{10mm} 1 - \theta(x) = \frac{[\ce{M_{N}}]}{[\ce{M_{A}}] + [\ce{M_{N}}]} \tag{5.1} \]
である。また,\(\ce{M_{A}}\),\(\ce{M_{N}}\) の平衡定数を \(K_{\mathrm{NA}}\) とすると
\[ K_{\mathrm{NA}}(x) = \frac{[\ce{M_{A}}]}{[\ce{M_{N}}]} = \frac{\theta(x)}{1 - \theta(x)} \tag{5.2} \]
となる。また,式 (4.11) の \(A_{\mathrm{model}}\) を測定値 \(A_{\mathrm{meas}}\) に入れ替え,\(D_{0}\),\(D_{n}\) は5.2.2節のフィッティング解析で得られた値を使うことにすれば,測定値から得られる \(\ce{M_{A}}\) のモル分率 \(\theta(x)\) は,
\[ \theta(x) = \frac{A_{\mathrm{meas}}(x) - D_{0}}{D_{n} - D_{0}} \tag{5.3} \]
となる。したがって,平衡定数 \(K_{\mathrm{NA}}\) の測定値は,
\[ K_{\mathrm{NA}}(x) = \frac{\theta}{1 - \theta} = \frac{A_{\mathrm{meas}}(x) - D_{0}}{D_{n} - A_{\mathrm{meas}}(x)} \tag{5.4} \]
で計算できる(再確認するが,\(K_{\mathrm{NA}}\) は PA Cyt c の2つのコンフォメーション間の平衡定数で,pH の関数である。PA Cyt c と水素イオンの結合定数 \(K_{\mathrm{H}}\)とは異なる)。以上より,\(\log_{10}K_{\mathrm{NA}}\) を \(\log_{10}[\ce{H+}]\)(\(= −\mathrm{pH}\))に対してプロットした Wyman プロットが得られる(図4C)。図4Cによれば,\(\log_{10}[\ce{H+}]\) が \(\log_{10}(1/K_{\mathrm{H}}) = −1.83\) の付近ではプロットがほぼ直線となり,1次関数のフィッティングによってその傾きは2.12と得られた。したがって,式 (4.18) より,図4Cで表示している pH 1–3 の範囲では,PA Cyt c の中性型→酸性型のコンフォメーション変化に伴う水素イオンの結合数変化の解析値は \(\Delta \bar{X} = 2.12\) 個という結果となった。
4.2節で説明したが,PA Cyt c の pH 変化に伴うコンフォメーション変化の Hill プロットも \(\log_{10}[\theta / (1 - \theta)]\) を \(\log_{10}[\ce{H+}]\) に対してプロットしたものであるので,結局のところ図4Cは Hill プロットでもある。したがって,Wyman プロットで得られた水素イオンの結合数変化 \(\Delta\bar{X} = 2.12\) と5.2.2節の Hill 係数 \(n = 2.06\) の値が近かったのは,偶然ではなく,解析に用いたモデルの上では近い内容のパラメータだったからである(Hill の協同性モデル式 (4.10) ではフィッティング範囲全域において \(n\) を定数とすることがモデルに含まれていたのに対し,Wyman プロットで得られる \(\Delta\bar{X}\) は単に Wyman プロット上の曲線の微係数としている点で,違いがある)。これらの2つの数値の間に発生した小さい差異は,用いたモデル関数やデータ範囲の違いによるものであると考えられる。
6. おわりに
多くの大学院生や研究者にとって,質量作用の法則は高校の化学で習う初歩的な事項であろう。そのため,多くの研究室では平衡定数を用いた諸計算は既知のことと見なされているようにも思われる。そういう事情が,質量作用の法則から開始し本稿の内容に至るような蛋白質平衡反応解析の基本原理の解説が実験書等でもあまり見られない理由かもしれないというのが,筆者の印象である。また,研究室の実験・解析の現場で,原理の理解はさておき,とにかくデータをコンピュータに入力して何らかの解離定数の数値を出せば良いという姿勢でもしも解析が進められているのであれば,本稿で指摘したようないくつかの誤りに陥ってしまうかもしれない。筆者からのメッセージのひとつは,実験者がデータ解析のためのモデルを立てる時は,実験データを処理するための数式の準備を隅々まで労を惜しまず自分の手で紙の上(あるいは,表計算ソフト,数式エディタ,数式処理ソフトウェア等でもよい)でやってみることが,実験対象の蛋白質が示す現象についてのアイディアを整理し,実験者の意図に沿って間違いなくデータ解析するのにしばしば有用である,ということである。本稿が,蛋白質の平衡反応解析の指導や実施の一助となれば幸いである。
補足. Wyman プロットの傾きについて
式 (4.18) は,2つのコンフォメーション間の遷移に伴う,蛋白質に結合しているリガンド数の変化を与えるものである。その内容を理解した気になるには,やはり,その式の導出過程をたどることが有効である。しかし,文献[4]や[5]に精通している読者ならともかく,蛋白質の平衡理論に精通していない多くの読者にとっては,それらの文献の中から導出過程を見つけて読み取るのは,あまり容易ではない。そこで,興味を持つ読者への便宜として,式 (4.18) の導出を説明することにする。
ここでの目標は,反応 (4.13) を基にして,蛋白質 \(\ce{M}\) のコンフォメーション0と1間の平衡定数のリガンド濃度依存性から,式 (4.18) を導出することである。\(\ce{M}\) と \(\ce{X}\) の平衡定数を
\[ K^{i}_{j} = \frac{[\ce{M_{\mathit{i}}X_{\mathit{j}}}]}{[\ce{M_{\mathit{i}}}]x^{j}}, \mspace{5mm} (i = 0, 1) \tag{A.1} \]
とする。インデックス \(i\) が \(\ce{M}\) のコンフォメーションを表している。各コンフォメーションの結合多項式は,
\[ P_{i} = \frac{1}{[\ce{M_{\mathit{i}}}]} \{ [\ce{M_{\mathit{i}}}] + [\ce{M_{\mathit{i}}X}] + \dots + [\ce{M_{\mathit{i}}X_{\mathit{N}}}] \} = 1 + K^{i}_{1}x + K^{i}_{2}x^{2} + \dots + K^{i}_{N}x^{N} \tag{A.2} \]
である。ここで,\(N\) は蛋白質1個あたりのリガンド結合部位数である(ただし,\(N\) は蛋白質が実際に持っている結合部位数より大きく取っても構わない。なぜなら,実際に起こらない反応段階については,結合定数を0としておくと考えれば,以下の導出過程に支障はないからである)。1モルあたりの \(\ce{M_{\mathit{i}}}\) に対して結合したリガンド \(\ce{X}\) のモル数 \(\bar{X}_{i}\) はリガンド濃度 \(x\) の関数であり,結合多項式を使って
\[
\begin{align}
\bar{X}_{i}
&= \frac
{1 \cdot [\ce{M_{\mathit{i}}X}] + 2 \cdot [\ce{M_{\mathit{i}}X_{2}}] + \dots + N \cdot [\ce{M_{\mathit{i}}X_{\mathit{N}}}]}
{[\ce{M_{\mathit{i}}}] + [\ce{M_{\mathit{i}}X}] + \dots + [\ce{M_{\mathit{i}}X_{\mathit{N}}}]}\
&= \frac
{K^{i}_{1}x + 2 \cdot K^{i}_{2}x^{2} + \dots + N \cdot K^{i}_{N}x^{N}}
{1 + K^{i}_{1}x + K^{i}_{2}x^{2} + \dots + K^{i}_{N}x^{N}}\
&= \frac
{\partial \ln P_{i}}
{\partial \ln x}
\end{align}
\tag{A.3}
\]
と書ける。よって,式 (A.2),(A.3) を使って式 (4.18) の微係数を計算すると,
\[
\begin{align}
\frac{\partial \ln K_{01}}{\partial \ln x}
&=
\frac{\partial}{\partial \ln x}
\left\{
\ln
\frac
{[\ce{M_{1}}] + [\ce{M_{1}X}] + \dots + [\ce{M_{1}X_{\mathit{N}}}]}
{[\ce{M_{0}}] + [\ce{M_{0}X}] + \dots + [\ce{M_{0}X_{\mathit{N}}}]}
\right\}\
&=
\frac{\partial}{\partial \ln x}
\ln
\frac
{[\ce{M_{1}}] \left( 1 + K^{1}_{1}x + \dots + K^{1}_{N}x^{N} \right)}
{[\ce{M_{0}}] \left( 1 + K^{0}_{1}x + \dots + K^{0}_{N}x^{N} \right)}\
&=
\frac{\partial \ln P_{1}}{\partial \ln x} - \frac{\partial \ln P_{0}}{\partial \ln x}\
&=
\bar{X}_{1}(x) - \bar{X}_{0}(x)
\end{align}
\tag{A.4}
\]
を得る。ここで,アポ型同士の反応商 \([\ce{M_{1}}]/[\ce{M_{0}}]\) は \(x\) に依存しない平衡定数となるので,微分をとることで消去されることも利用している。式 (A.4) の内容を読み込めば,リガンド濃度が \(x\) の時における,1モルあたりのコンフォメーション1の蛋白質に結合するリガンドのモル数と,1モルあたりのコンフォメーション0に結合するリガンドのモル数の差を,最後の行が表している。また,質量作用の法則を適用できる結合反応系であれば,各反応段階の結合定数の詳細な情報がなくても,コンフォメーション0,1間の平衡定数のリガンド濃度依存性の情報だけでリガンドの結合数の差分を求めることができるというのが,Wyman の理論から得られる式 (A.4) の効用である。
文献
- Germond, A. et al, Biophys. Rev. 8, 121–138 (2016)
- Klotz, I.M., Ligand-receptor energetics. Wiley & Sons, New York (1997)
- Cantor, C.R. & Schimmel, P.R., Biophysical Chemistry II: Techniques for the study of biological structure and function. W.H. Freeman, San Francisco (1980)
- Wyman, J. & Gill, S. J., Binding and linkage. University Science Books, Mill Valley (1990)
- Wyman, J., Adv. Protein Chem. 19, 223–286 (1964)
- Myer, Y.P. & Saturno, A.F., J. Protein Chem. 10, 481–494 (1991)
- Adair, G.S. et al., J. Biol. Chem. 63, 529–545 (1925)
- Wazawa, T. et al., Biophys. Chem. 151, 160–169 (2010)
- Miyashita, Y. et al., Biophys. J. 104, 163–172 (2013)
- Horikawa, K. et al., Nat. Methods 7, 729–732 (2010)
- Hill, A.V., J. Physiol. (suppl), 40, iv–vi (1910)


