概要

蛋白質科学会アーカイブ, 1, e031 (2008)「タンパク質科学実験メモ：van’t Hoff の式についてのメモ3題」の第2題として「van’t Hoff プロットから得られる \({\Delta}H = 〇〇\,\textrm{kcal}\,\textrm{mol}^{-1}\) の “\(\textrm{mol}\)” は何でしょうか？」という質問が示されており，その解説文に「“\(\textrm{mol}\)” は気体定数（\(R = 8.314\,\textrm{J}\,\textrm{mol}^{-1}\,\textrm{K}^{-1}\)）からきている」という記述がある。化学反応の \(\Delta H\)（厳密には，標準反応エンタルピー \({\Delta}_{\textrm{r}}H^{\circ}\)）の単位に含まれている \(\textrm{mol}\) が気体定数の単位に含まれる \(\textrm{mol}\) に由来するという説明は難解であり，逆に，気体定数の単位の \(\textrm{mol}\) は物質量を表さないのだろうか？という新たな疑問を生じさせる可能性がある。本稿は，標準反応エンタルピーの単位に含まれる \(\textrm{mol}\) の物理的な意味を明確にし，平衡定数や標準反応物理量を定義するには化学反応式を明示することが必須であることを理解するための「オピニオン」である。

1. 反応進行度

平衡定数の温度依存性から van’t Hoff プロットによって得られる \(\Delta H\) の正確な名称は「標準反応エンタルピー」であり，IUPAC 発行のGreen Book[1] には \(\Delta_{\textrm{r}}H^{\circ}\) と記されている。下付添字 \(_{\textrm{r}}\) は化学反応（reaction）を意味し，右上の記号 \(^{\circ}\) は標準状態を表している。右上の \(^{\circ}\) は小さい記号ではあるが，この記号の有無によって物理的な意味が大きく変わるので，van’t Hoff プロットから得られるエンタルピーには必ず \(^{\circ}\) を付けなければならない。一般に，\(\Delta\) は差を意味するが，\(\Delta_{\textrm{r}}\) は差ではなく \(\Delta_{\textrm{r}} \equiv \partial / \partial \xi\) という演算子記号を表しており，\(\xi\) は「反応進行度」（extent of reaction）である[1]。

反応進行度は化学反応に関与する化学種（A とする）の物質量（単位：\(\textrm{mol}\)）の変化を量論数（化学量数とも呼ばれる無次元量）で割ったものであり，次式で定義される。

\[ \xi = \frac{n_{\mathrm{A}} - n_{\mathrm{A},0}}{v_{\mathrm{A}}} \tag{1} \]

なお，\(n_{\mathrm{A},0}\) は反応開始時の化学種 A の物質量，\(n_{\mathrm{A}}\) は任意の時刻での化学種 A の物質量，\(v_{\mathrm{A}}\) は化学種 A の量論数である（化学反応式の係数は，通常，量論係数と呼ばれる。量論数は化学量数とも呼ばれ，反応物（始原系）については量論係数の負値，生成物については正値で定義される。たとえば，化学反応 \(\ce{2A -> 3B}\) の場合，\(v_{\mathrm{A}} = -2\)，\(v_{\mathrm{B}} = 3\) である）。反応進行度は化学種には依存せず，反応物あるいは生成物のどの化学種についても同じ値になる。物質量の単位は \(\textrm{mol}\) であり，量論数は無次元量であるから，反応進行度の単位は \(\textrm{mol}\) である。反応開始時はすべての化学種について \(n_{\mathrm{A}} = n_{\mathrm{A},0}\) であるから \(\xi = 1\,\textrm{mol}\) である。しかし，最大値（反応の終点）は必ずしも \(\xi_{\textrm{max}} = 1\,\textrm{mol}\) とならない点に注意する必要がある（反応の終点とは，少なくとも反応物の1つが尽きた時点である）。たとえば，次の化学反応

\[ \ce{2A + 3B -> 生成物} \tag{2} \]

を初期物質量 \(n_{\mathrm{A},0} = 4\,\textrm{mol},\,n_{\mathrm{B},0} = 6\,\textrm{mol}\) で開始すると，反応物がすべて消費された時点での反応進行度は \(\xi_{\textrm{max}} = 2\,\textrm{mol}\) となる。また，初期物質量 \(n_{\mathrm{A},0} = 3\,\textrm{mol},\,n_{\mathrm{B},0} = 6\,\textrm{mol}\) で開始した場合は，反応終了時の物質量が \(n_{\mathrm{A},\textrm{max}} = 0\,\textrm{mol},\,n_{\mathrm{B},\textrm{max}} = 1.5\,\textrm{mol}\) となるから \(\xi_{\textrm{max}} = 1.5\,\textrm{mol}\) となる。初期物質量が \(n_{\mathrm{A},0} = 1\,\textrm{mol},\,n_{\mathrm{B},0} = 6\,\textrm{mol}\) の場合は \(\xi_{\textrm{max}} = 0.5\,\textrm{mol}\) となる。ちなみに，化学反応が開始から終点までの間のどこまで進行したかを示す量は「反応率」（degree of reaction）であり，\(\xi / \xi_{\textrm{max}}\) で定義され，数値の範囲は \(0 \le \xi / \xi_{\textrm{max}} \le 1\) である。なお，化学反応式の量論係数と同じ値の物質量で反応を開始した場合は，反応終点の反応進行度は必ず \(\xi_{\textrm{max}} = 1\,\textrm{mol}\) になる。

反応進行度の単位が物質量の単位と同じ \(\textrm{mol}\) であることから，反応進行度は化学反応にかかわる化学種の物質量を反映していると解釈されがちであるが，上述した具体例のいずれの場合も，化学反応により変化した物質量は反応進行度に対応していない。原因は式 (1) から明らかであり，式 (1) の分母の大きさ（量論係数）が1ではない化学種の物質量変化は反応進行度に一致しない。以下では，反応進行度の単位（\(\textrm{mol}\)）の物理的な意味について考える。

化学反応が反応系から生成系に向けて1回進行するとき，反応物として消費される物質量あるいは生成物として生じる物質量は化学種ごとに異なる。反応式の係数が大きいほど物質量の変化は大きく，物質量の変化の大きさの比は化学反応式の係数の比に対応するから，式 (1) の分母の量論数は，化学種間での物質量変化の相違を解消する役割を果たしている。たとえば，化学反応式 (2) により，1回の反応で2分子が消費される化学種 A の量論数は \(-2\) であるから，化学種 A が100分子消費されたとき，反応の回数は \((-100) / (-2) = 50\) 回である。同じ化学反応1回につき3分子が消費される化学種 B は，化学種 A が100分子消費される間に150分子消費される。このときの反応の回数も，当然ながら \((-150) / (-3) = 50\) 回である。分子の個数を \(\textrm{mol}\) 単位で表現すると，量論数 \(-2\) の化学種が \(100\,\textrm{mol}\)（同時に，量論数 \(-3\) の化学種が \(150\,\textrm{mol}\)）消費されるとき，化学反応が \(50\,\textrm{mol}\) 回，つまり，Avogadro 定数の50倍の回数（\(3.01 \times 10^{25}\) 回）進行することになる。この \(50\,\textrm{mol}\) という回数が反応進行度 \(\xi = 50\,\textrm{mol}\) の物理的な意味である。したがって，反応進行度の単位 \(\textrm{mol}\) の由来は物質量であるが，量論数で割られた時点で，物理的な意味が反応の回数に切り替わっている。

2. 標準反応エンタルピー

上述した記号 \(\Delta_{\textrm{r}}\) の定義により，標準反応エンタルピー \({\Delta}_{\textrm{r}}H^{\circ}\) は

\[ {\Delta}_{\textrm{r}}H^{\circ} = \frac{\partial H^{\circ}}{\partial\xi} \tag{3} \]

となる（厳密には，定温，定圧条件を付けて \({\Delta}_{\textrm{r}}H^{\circ} = (\partial H^{\circ} / {\partial\xi})_{T,p}\) と書く）。式の右辺の形から \({\Delta}_{\textrm{r}}H^{\circ}\) の意味を解釈すると「反応系全体の標準エンタルピー \(H^{\circ}\)（単位：\(\textrm{J}\)）の反応進行度（単位：\(\textrm{mol}\)）に対する微係数（勾配）」となるが，表現を替えれば，「単位反応進行度（\(\textrm{mol}\)）あたり，（標準状態の）化学反応系に出入りする熱量（\(\textrm{J}\)）」となる。\(H^{\circ}\) の単位が \(\textrm{J}\) で，\(\xi\) の単位が \(\textrm{mol}\) であるから，\({\Delta}_{\textrm{r}}H^{\circ}\) の単位は \(\textrm{J}\,\textrm{mol}^{-1}\) である。つまり，\({\Delta}_{\textrm{r}}H^{\circ}\) は，化学反応が \(6 \times 10^{23}\) 回（＝ \(1 \textrm{mol}\) 回＝単位反応進行度）進行する際に，系に出入りする熱（発熱あるいは吸熱）を表す物理量である。以上より，\({\Delta}_{\textrm{r}}H^{\circ}\) の単位 \(\textrm{J}\,\textrm{mol}^{-1}\) の \(\textrm{mol}\) は，化学反応式で表された反応が進行した回数を（\(\textrm{mol}\) 単位で）表現していることがわかる。

記号 \(\Delta_{\textrm{r}}\) により微分されている系全体の標準エンタルピー \(H^{\circ}\) は系特有の定数ではなく，反応進行度（したがって，系の組成）に依存する物理量である。\(H^{\circ}\) は純粋な化学種 \(i\) の標準エンタルピー（単位：\(\textrm{J}\)）により，

\[ H^{\circ} = \sum_{i} H^{\circ}_{i} \tag{4} \]

で与えられる。化学種 \(i\) の標準エンタルピー \(H^{\circ}_{i}\) は反応中の化学種 \(i\) の物質量 \(n_{i}\)（単位：\(\textrm{mol}\)）と純粋状態の化学種 \(i\) の標準モルエンタルピー \(H^{\circ}_{i,m}\)（単位：\(\textrm{J}\,\textrm{mol}^{-1}\)）の積 \(n_{i} H^{\circ}_{i,m}\) であるから，\(H^{\circ}\) は

\[ H^{\circ} = \sum_{i} n_{i} H^{\circ}_{i,m} \tag{5} \]

で表される（純物質のモル物理量と部分モル物理量は等しいので，標準モルエンタルピー \(H^{\circ}_{i,m}\) を用いた）。反応進行度の定義式 (1) より，

\[ n_{i} = v_{i}\xi + n_{i,0} \tag{6} \]

となるから，式 (6) を式 (5) に代入して，

\[ H^{\circ} = \left(\sum_{i} v_{i} H^{\circ}_{i,m}\right) \xi + \sum_{i} n_{i,0} H^{\circ}_{i,m} \tag{7} \]

を得る。式 (3) に従って，式 (7) を \(\xi\) で微分したものが \({\Delta}_{\textrm{r}}H^{\circ}\) であるから，

\[ {\Delta}_{\textrm{r}}H^{\circ} = \frac{\partial H^{\circ}}{\partial \xi} = \sum_{i} v_{i} H^{\circ}_{i,m} \tag{8} \]

が成り立つ。式 (8) の右辺の \(v_{i}\) と \(H^{\circ}_{i,m}\) はいずれも，進行している化学反応の化学種の組成（濃度）や反応進行度とは無関係な量であり，化学反応式が示されれば決まる量である。なお，具体的に式 (8) の値を計算する際には，\(H^{\circ}_{i,m}\) の代わりに標準生成エンタルピー \(\Delta_{\textrm{f}} H^{\circ}_{i}\)（単位：\(\textrm{J}\,\textrm{mol}^{-1}\)）を用いればよい。

3. 標準エンタルピーの差と標準反応エンタルピー

\({\Delta}_{\textrm{r}}H^{\circ}\) を「生成系と反応系の標準エンタルピーの差」と記している解説を見かけることがあるが，\({\Delta}_{\textrm{r}}H^{\circ}\) が差を表していないことは式 (3) の定義から明らかである。量論係数に等しい物質量の反応物を準備して反応を開始させるとき，反応物の化学種を \(j\)，生成物の化学種を \(k\) で表すと，各化学種の物質量と量論数の間には次の関係が成り立つ。

\[ n_{j,0} = -v_{j} \times (\textrm{mol}) \tag{9} \]

\[ n_{k,\textrm{max}} = v_{k} \times (\textrm{mol}) \tag{10} \]

それぞれの右辺に付けた \((\textrm{mol})\) は両辺の単位を \(\textrm{mol}\) に一致させるために記されている。反応開始時（\(\xi = 0\,\textrm{mol}\)）と反応終点（\(\xi = 1\,\textrm{mol}\)）での全系の標準エンタルピーはそれぞれ，

\[ H^{\circ}(\xi = 0) = \sum_{j} n_{j,0} H^{\circ}_{j,\textrm{m}} = - \sum_{j} v_{j} H^{\circ}_{j,\textrm{m}} \times (\textrm{mol}) \tag{11} \]

\[ H^{\circ}(\xi = 1) = \sum_{k} n_{k,\textrm{max}} H^{\circ}_{j,\textrm{m}} = \sum_{k} v_{k} H^{\circ}_{k,\textrm{m}} \times (\textrm{mol}) \tag{12} \]

となるので，全系の標準エンタルピーの反応終点と反応開始時の差は

\[ H^{\circ}(\xi = 1) - H^{\circ}(\xi = 0) = \sum_{k} v_{k} H^{\circ}_{k,\textrm{m}} \times (\textrm{mol}) + \sum_{j} v_{j} H^{\circ}_{j,\textrm{m}} \times (\textrm{mol}) = \sum_{i} v_{i} H^{\circ}_{i,\textrm{m}} \times (\textrm{mol}) \tag{13} \]

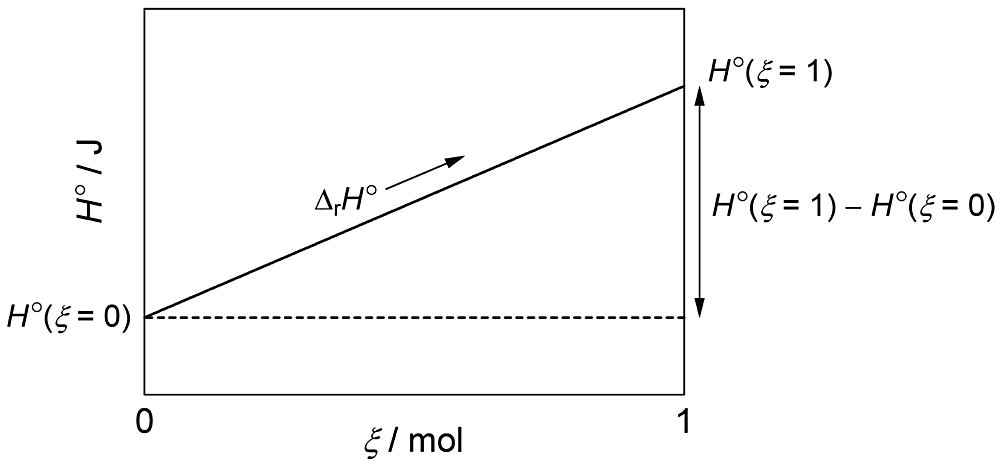
となる。\(H^{\circ}(\xi = 1) - H^{\circ}(\xi = 0)\) と \({\Delta}_{\textrm{r}}H^{\circ}\)（式 (8)）の値は同じであるが，単位が異なるから，同じ物理量ではない。\(H^{\circ}(\xi = 1) - H^{\circ}(\xi = 0)\) と \({\Delta}_{\textrm{r}}H^{\circ}\) の相違は図1により理解できる。

図1の \(x\) 軸の増分1に対する \(y\) 軸の増分が \(H^{\circ}(\xi = 1) - H^{\circ}(\xi = 0)\) であるから，\(H^{\circ}(\xi = 1)\) と \(H^{\circ}(\xi = 0)\) を結ぶ線の勾配を表す \({\Delta}_{\textrm{r}}H^{\circ}\) は \(H^{\circ}(\xi = 1) - H^{\circ}(\xi = 0)\) と（異なる物理量であるにもかかわらず）同じ値になるのである。比較的古いテキストには，\({\Delta}_{\textrm{r}}H^{\circ}\) を標準反応エンタルピー変化，あるいは標準反応エンタルピー差と呼ぶものが多いが，正式な名称は標準反応エンタルピーである。「変化」あるいは「差」を付けると，\({\Delta}_{\textrm{r}}H^{\circ}\) ではなく \(H^{\circ}(\xi = 1) - H^{\circ}(\xi = 0)\) の意味に誤解されやすくなるので，\({\Delta}_{\textrm{r}}H^{\circ}\) を変化や差と呼ぶべきではない。

4. 化学反応式と平衡定数および標準反応熱力学量との関係

式 (8) の右辺に量論数が含まれているから，\({\Delta}_{\textrm{r}}H^{\circ}\) は現象（化学反応）固有の数値ではなく，化学反応式の書き方（量論係数の記し方）に依存する点に注意する必要がある。たとえば，ベンゼン（\(\ce{C6H6}\)）と酸素の化学反応（完全燃焼）

\[ \ce{2C6H6(g) + 15O2(g) -> 12CO2(g) + 6H2O(g)} \tag{14} \]

の標準反応エンタルピーは \({\Delta}_{\textrm{r}}H^{\circ} = -6339\,\textrm{kJ}\,\textrm{mol}^{-1}\) であるが，この反応を

\[ \ce{C6H6(g) + \frac{15}{2}O2(g) -> 6CO2(g) + 3H2O(g)} \tag{15} \]

と表すと，\({\Delta}_{\textrm{r}}H^{\circ} = -3170\,\textrm{kJ}\,\textrm{mol}^{-1}\) となる。このように，\({\Delta}_{\textrm{r}}H^{\circ}\) は化学反応式が示されてはじめてその値が意味をもつ物理量である。2つの化学反応式は同じ現象（ベンゼンの完全燃焼）を表しているから，もし，\({\Delta}_{\textrm{r}}H^{\circ}\) の単位の中の mol がある1つの化学種の物質量 1 mol に結びついているならば，化学反応式の書き方によらず同じ値になるはずであるが，反応式の書き方（係数の大きさ）に依存していることからも，mol が特定の化学種の物質量に対応していないことがわかる。

上記の点に関連して，文献[1]，pp. 69～70の表中の標準反応熱力学量（\(\Delta_{\textrm{r}}G^{\circ}\)：標準反応 Gibbs エネルギー，\({\Delta}_{\textrm{r}}H^{\circ}\)：標準反応エンタルピー，\({\Delta}_{\textrm{r}}S^{\circ}\)：標準反応エントロピー）および平衡定数（\(K^{\circ}\)：標準平衡定数，\(K_{p}\)：圧力に基づいた平衡定数，\(K_{c}\)：濃度に基づいた平衡定数，\(K_{m}\)：質量モル濃度に基づいた平衡定数）には，「この量を適用するにあたっては，どの反応であるかを特定しなければならない。（英語版では “The reaction must be specified for which this quantity applies.”）」と注意書きが記されている。日本語訳を言い換えると，「この量を適用する化学反応を明記しなければならない。」となるが，以下で，この文の意味を明らかにする。

反応物（X）と生成物（Y）の量論比が2：1である化学反応について，化学反応が平衡に到達したときの化学種 X の濃度 \(\ce{[X]}\) と化学種 Y の濃度 \(\ce{[Y]}\) を測定して平衡定数を決定する作業を考える。この反応の化学反応式を

\[ \ce{2X -> Y} \tag{16} \]

と書けば，平衡定数 \(K_c\) は

\[ K_{c1} = \frac{[\textrm{Y}]}{[\textrm{X}]^{2}} \tag{17} \]

で与えられる。同じ反応の化学反応式を

\[ \ce{X -> \frac{1}{2}Y} \tag{18} \]

と書くと，この表記での平衡定数 \(K_c\) は

\[ K_{c2} = \frac{[\textrm{Y}]^{1/2}}{[\textrm{X}]} \tag{19} \]

となる。実測される平衡濃度 \(\ce{[X]}\) と \(\ce{[Y]}\) は，化学反応式の書き方に依存しないから，

\[ K_{c2} = \sqrt{K_{c1}} \tag{20} \]

が成り立つ。2つの平衡定数の値は異なるが，一方が正しく他方が誤りというわけではなく，化学反応式を式 (16) で表せば \(K_{c1}\) が，化学反応式を式 (18) で表せば \(K_{c2}\) が正しい平衡定数である。化学反応式を明示せず平衡定数だけを示すと，その平衡定数がどのように定義されたかわらかないため数値の意味が失われてしまう。この問題を回避するために，Green Book は化学反応を明記するよう要請しているのである。さらに，平衡定数の温度依存性を測定し，van’t Hoff の式（プロット）から標準反応エンタルピー\({\Delta}_{\textrm{r}}H^{\circ}\)を決定する状況を考えてみる。平衡定数 \(K_{c1}\) については，

\[ \frac{\mathrm{d} \ln K_{c1}}{\mathrm{d}(1/T)} = - \frac{\Delta_{\textrm{r}}H^{\circ}_{1}}{R} \tag{21} \]

から \(\Delta_{\textrm{r}}H^{\circ}_{1}\) が得られ，平衡定数 \(K_{c2}\) については，

\[ \frac{\mathrm{d} \ln K_{c2}}{\mathrm{d}(1/T)} = - \frac{\Delta_{\textrm{r}}H^{\circ}_{2}}{R} \tag{22} \]

から \(\Delta_{\textrm{r}}H^{\circ}_{2}\) が得られるが，式 (20)の関係より，

\[ \frac{\mathrm{d} \ln K_{c2}}{\mathrm{d}(1/T)} = \left( \frac{1}{2} \right) \frac{\mathrm{d} \ln K_{c1}}{\mathrm{d}(1/T)} = - \frac{\Delta_{\textrm{r}}H^{\circ}_{1}}{2R} \tag{23} \]

となり，

\[ \Delta_{\textrm{r}}H^{\circ}_{1} = 2 \Delta_{\textrm{r}}H^{\circ}_{2} \tag{24} \]

が成り立つ。\(\Delta_{\textrm{r}}H^{\circ}_{1}\) が \(\Delta_{\textrm{r}}H^{\circ}_{2}\) の2倍となるが，注目している化学反応の標準反応エンタルピー \(\Delta_{\textrm{r}}H^{\circ}\) として，一方が正しく他方が誤りというわけではなく，対応する化学反応式について，それぞれが正しい標準反応エンタルピーである。これは，先に示したベンゼンと酸素の反応に関する2つの \(\Delta_{\textrm{r}}H^{\circ}\) について述べたことと同じである。式 (24) は，化学反応式 (16) が 1 mol 回進行する際の熱の出入りが，化学反応式 (18) が 1 mol 回進行する際の熱の出入りの2倍であることを意味しており，\(\Delta_{\textrm{r}}H^{\circ}\) の単位 \(\textrm{J}\,\textrm{mol}^{-1}\) の \(\textrm{mol}\) が明示された化学反応式が進行した回数にあたるという理解に合致する。

以上の議論から，平衡定数の温度依存性測定 → van’t Hoff プロット作成 → 標準反応エンタルピー決定というプロセスは，一貫して1つの化学反応式にもとづいて行われるべきであり，平衡定数や標準反応エンタルピーなどの数値を報告する際には，必ず化学反応式を明記しなければならないことが理解できよう。

あとがき

研究分野が近い “同業者” 間での会話では，「この反応の平衡定数は3.0でエンタルピー変化は 50 kJ である」という表現を使いがちであるが，このような表現はたくさんの曖昧な点を含んでいる。まず，平衡定数は標準状態のとり方で値が変わるから，平衡定数を示す際には必ず標準状態を明確にしなければならない。また，「エンタルピー変化」という用語は存在せず，正しくは「標準反応エンタルピー」であり，“標準” を付けず「反応エンタルピー」と表現してしまうと別の物理量になってしまう。また，50 kJ は熱量のイメージには近いが，正確には，\(50\,\textrm{kJ}\,\textrm{mol}^{-1}\) と正しい単位を付けて表現しなければならない。そして，なによりも大事なのは，「この反応」を表す化学反応式を明示しなければ，平衡定数の値も標準反応エンタルピーの値も意味をもたないという点である。\(50\,\textrm{kJ}\,\textrm{mol}^{-1}\) の mol や \(\Delta_{\textrm{r}}H^{\circ}\) の \(^{\circ}\) が，単なる記号書式の約束事ではなく，情報を正確に発信・受信するための “必需品” であり，これらの単位や記号の物理的な意味や根拠を理解することは，基礎事項の理解と同時に，実験データを正しく評価・考察する眼を養うためにも重要である。

なお，本稿を著すにあたり，蛋白質科学会アーカイブの当該記事の著者（高橋 克忠 氏）に事前に本稿の趣旨を連絡し，内容について了解いただくと同時に，本稿の投稿をお勧めいただいたことに感謝申しあげます。

文献

1. E. R. Cohen, T. Cvitaš, J. G. Frey, B. Holmström, K. Kuchitsu, R. Marquardt, I. Mills, F. Pavese, M. Quack, J. Stohner, H. L. Strauss, M. Takami, and A. J. Thor, Quantities, Units and Symbols in Physical Chemistry —The IUPAC Green Book—, 3rd ed., RSC Publishing, Cambridge, 2007.
   日本語版：産業技術総合研究所計量標準総合センター訳，物理化学で用いられる量・単位・記号，第3版（講談社サイエンティフィク，2009年）。日本語版は下記 URL から入手可能。
   https://unit.aist.go.jp/nmij/public/report/translation/IUPAC/iupac/iupac_green_book_jp.pdf