イントロダクション
分子動力学シミュレーション(Molecular Dynamics: MD)は、粒子間に働く相互作用および力を計算し、運動方程式を解くことで、粒子の運動を求める方法である。溶媒を含む全ての相互作用を考慮し、古典力学の範囲内で生体分子の動的構造を計算し、その計算結果を解析することで様々な物理量を求めることができる。タンパク質や核酸などの生体分子の動的構造や相互作用を原子解像度で調べる手法として生命科学において広く用いられている。特に、MD シミュレーションでは各状態での安定性または存在確率を求めることができ、これらは自由エネルギー地形と呼ばれている。自由エネルギー地形を詳細に分析することで、生体分子の構造変化や分子機構を理解することができる。
しかし、生体分子の自由エネルギー地形は多数の局所安定状態を持った複雑な形状をしており、限られた計算時間ではシミュレーションが局所安定状態に捕らわれてしまう。この問題を避けるために、拡張アンサンブル法などの効率的なサンプリング法が用いられている。拡張アンサンブル法では、エネルギーあるいは事前に定義された反応座標における一次元ランダムウォークを実現することで、状態空間を広く探索する。
様々な拡張アンサンブル法が提案されているが、計算コストを抑えつつ、タンパク質構造を効率的に探索する計算手法が望ましい。そのような計算手法として、我々は Gaussian accelerated MD(GaMD)法(文献1,2)と Replica-Exchange Umbrella Sampling(REUS)法(文献3,4)の2つの拡張アンサンブル法を組み合わせた Gaussian accelerated Replica-Exchange Umbrella Sampling(GaREUS)法を提案した(文献5)。GaREUS 法では、GaMD 法によってタンパク質の構造柔軟性を向上させ、同時に REUS 法によって反応座標空間を広く探索する。GaREUS 法で得られたトラジェクトリーから二段階の Reweighting を行うことで、正確な自由エネルギー地形を求めることが出来る。GaREUS 法は、理化学研究所で開発している MD シミュレーションソフトウェア「GENESIS」(文献6,7)に実装されており,GPU ワークステーションからスーパーコンピュータまで様々な計算機を用いた計算が可能である。本稿では GaREUS 法を用いた自由エネルギー地形の計算方法を説明する。
計算機・ソフトウェア
GaREUS 法の実行には MD シミュレーションソフトウェア GENESIS を用いる。GENESIS はオープンソフトウェア(LGPLv3)として公開しており、無料で利用できる。最新版は GENESIS のウェブサイトから入手可能である。
GENESIS をコンパイル・実行するには、OS として Linux、C コンパイラおよび Fortran コンパイラとして gcc、gfortran または Intel Fortran/C++ compiler、開発環境として GNU autoconf、並列計算ライブラリーとして OpenMPI、数学ライブラリーとして BLAS と LAPACK が必要である。GPU を利用する場合は CUDA ライブラリーも必要となる。詳細な必要条件やコンパイル方法は GENESIS のウェブサイトかマニュアルを参考にしてほしい。
GaREUS 法では複数のレプリカ(MD シミュレーション)を同時に実行する必要があるため、複数の計算ノードを持ったコンピュータクラスターかスーパーコンピュータを用いる。Intel 社、AMD 社、富士通(A64FX)の CPU を搭載しており、GPU を利用する場合は、CUDA 対応の nVIDIA 社の GPU を搭載したものを用いる。例えば、10レプリカの計算をする場合、8CPU コア以上を搭載した計算ノードが10個必要となる。複数ノードを用いた計算にはバッチジョブシステムの利用が必要だが、利用方法はソフトウェアや計算機システムごとに大きく異なるため、各システムのマニュアルを参照するか管理者に問い合わせてほしい。
計算手順
- 生体分子モデルのセットアップ
- 構造最適化と平衡化
- GaMD パラメータの決定
- 本計算
- 解析
実験の詳細
1. 生体分子モデルのセットアップ
例として Alanine Tripeptide を用いる(図1)。GaREUS の反応座標として、残基1の酸素と残基3の水素の原子間距離を用いる(図1の点線丸)。Alanine Tripeptide に水分子を加え、一辺 50 Å 程度のボックスを作る。ここでは力場パラメータとして CHARMM 力場の C36 を用いる。タンパク質のセットアップについては、GENESIS のウェブサイトのチュートリアル(Level 1: Basic tutorials)および文献8で説明されているので、そちらを参照していただきたい。
2. 構造最適化と平衡化
セットアップで得た構造は原子同士が衝突していたり、不安定な構造になっていたりすることがある。ポテンシャルエネルギーが極端に高すぎるため、そのまま MD 計算をしてしまうとシステムが崩壊してしまう。構造最適化によってポテンシャルエネルギーを下げ、原子の衝突を取り除く。このとき、対象としているタンパク質やリガンドの位置や距離に拘束をかけ、分子が動かないようにする。GENESIS では最急降下法で構造最適化を行う。
構造最適化が終わったシステムは分子に速度が与えられていない絶対零度の状態になっている。分子に初期速度を与え、システムの温度を標的温度までゆっくりと上昇させる。GENESIS では Langevin 熱浴で等温等積(NVT)の MD 計算を行う。
次に、等温等圧(NPT)で MD 計算を行い、システムの体積を調整する。体積の時間変化を確認し、体積があまり変化しなくなるまでシミュレーションを行う。GENESIS では Bussi の方法で温度・圧力を調整する。
最後に、本計算と同じ熱力学条件で平衡化を行う。平衡化に必要なステップ数はシステムによって異なるため、温度、体積、ポテンシャルエネルギーの時間変化がドリフトしていないか注意する。構造のトラジェクトリーを見て、構造が壊れていないかも確認する。Root-Mean-Square Displacement(RMSD)や Root-Mean-Square Fluctuation(RMSF)等で時間変化を確認し、あまり変化しなくなったところで平衡化を終える。構造最適化および平衡化についても GENESIS のウェブサイトのチュートリアル(Level 1: Basic tutorials)および文献8で GENESIS のインプットファイルも含めて詳細な説明されているので、そちらを参照していただきたい。
3. GaMD パラメータの決定
GaMD ではシステムの本来のポテンシャル \(U(x)\) にバイアス \(\Delta U^{\mathrm{GaMD}}(U(x))\) を加えることで、エネルギー障壁を下げる(図2の式(1)および図3)。\(U(x)\) が閾値 \(E\) よりも小さいときのみ調和ポテンシャル型のバイアスを加え、それ以外は何も足さない(図2の式(2))。このようにすることで、システムを局所安定な状態に捉えられることなく、状態空間を広くサンプリングすることができるようになる。\(U’(x)\) が連続関数かつ \(U(x)\) における大小関係(\(U(x_{1}) < U(x_{2})\) ならば \(U’(x_{1}) < U’(x_{2})\))を維持するために、閾値 \(E\) はポテンシャルの最大値 \(U_{\mathrm{max}}\) と最小値 \(U_{\mathrm{min}}\) によって条件づけられる(図2の式(3))。また、正確な Reweighting のために、\(U’(x)\) の分散は図2の式(4)を満たす必要がある。ここで、\(U_{\mathrm{ave}}\) と \(\sigma_{U}\) はそれぞれポテンシャルの \(U(x)\) の平均値と分散で、\(\sigma_{0}\) はユーザーが設定する分散の最大値である。\(k_{0}\) を \(k(U_{\mathrm{max}} - U_{\mathrm{min}})\) と定義すると、閾値 \(E\) を下限 \(U_{\mathrm{max}}\) に設定する場合、\(k_{0}\) は図2の式(5)で決定する。ここでは最小限の説明しかしていないが、GaMD のパラメータの詳細は Miao の原著論文(文献1,2)を参照していただきたい。
GaMD では二面角とそれ以外の全ポテンシャルエネルギーを別々にブーストする「デュアルブースト」が利用できる(文献9)。二面角のブーストによってタンパク質の構造柔軟性を向上し、構造探索を加速する。同時に、二面角以外の全ポテンシャルエネルギーをブーストすることで、タンパク質近傍の水分子の運動等を加速し、ケージング効果等を回避する。デュアルブーストの場合は、上記の GaMD パラメータが二面角とそれ以外の全ポテンシャルエネルギーに対してそれぞれ必要となる。
\(k\) と \(E\) を決めるには \(U_{\mathrm{max}}\), \(U_{\mathrm{min}}\), \(U_{\mathrm{ave}}\), \(\sigma_{U}\) が必要となるが、系のポテンシャルエネルギー地形が複雑なため、一般的にはこれらは事前にわからない。まずブーストをかけずに MD 計算を行い、ポテンシャルの形状を探索し、これらのパラメータを決める。通常の MD のインプットに加えて、[GAMD] セクションを追加する(図4)。それぞれのパラメータの意味は、gamd は GaMD をするか否か、boost=no はブーストしない、boost_type=DUAL はデュアルブーストを用いる、thresh_type=LOWER は式(3)の下限 \(E_{\mathrm{max}}\) を用いる、sigma0_dih と sigma0_pot はそれぞれ二面角とそれ以外のポテンシャルの \(\sigma_{0}\) という意味である。update_period は GaMD のパラメータ \(U_{\mathrm{max}}\), \(U_{\mathrm{min}}\), \(U_{\mathrm{ave}}\), \(\sigma_{U}\) を更新する頻度で、この段階では MD 計算のステップ数を同じにしておく。
計算が終わると [OUTPUT] の gamdfile で指定したファイルに図5のような結果が出力される。POT_MAX, POT_MIN, POT_AVE, POT_DEV が二面角以外のポテンシャルの \(U_{\mathrm{max}}\), \(U_{\mathrm{min}}\), \(U_{\mathrm{ave}}\), \(\sigma_{U}\) であり、POT_TH, POT_KC, POT_KC0 はそれらから計算した \(E\) と \(k\) となっている。同様に DIH が付いたものは二面角のパラメータである。
初期パラメータが決まったら、実際に GaMD のブーストポテンシャルを加えながらパラメータを更新していく。[GAMD] で boost=yes とし、pot_max や dih_max 等に先ほどの gamdfile に出力された初期パラメータを入力する(図6)。ブーストポテンシャルを加えることで探索できるポテンシャル表面の領域が広がり、\(U_{\mathrm{max}}\), \(U_{\mathrm{min}}\), \(U_{\mathrm{ave}}\), \(\sigma_{U}\) が変化する。update_period=500 とすると500ステップごとに、pot_max や dih_max 等を新たな \(U_{\mathrm{max}}\), \(U_{\mathrm{min}}\), \(U_{\mathrm{ave}}\), \(\sigma_{U}\) を基に更新する。パラメータの更新を繰り返すことで、探索できるポテンシャル表面が徐々に広くなっていき、より良い \(U_{\mathrm{max}}\), \(U_{\mathrm{min}}\), \(U_{\mathrm{ave}}\), \(\sigma_{U}\) が見つかりやすくなる。
更新されたパラメータは update_period ごとに gamdfile で指定されたファイルに出力される(図7)。パラメータの時間変化を確認し、あまり変化しなくなったところで計算を終える。出力の最後の行の値で GaMD のパラメータを決定し、以降は変化させない。
4. 本計算
GaREUS では、GaMD のブーストポテンシャル \(\Delta U^{\mathrm{GaMD}}(U(x))\) を加えつつ、REUS シミュレーションを行う(図2の式(6))。\(\Delta U_{i}^{\mathrm{REUS}} (\xi(x))\) は REUS のバイアスポテンシャル、\(\xi(x)\) は REUS で用いる反応座標、\(i\) はレプリカの番号である。\(\Delta U_{i}^{\mathrm{REUS}} (\xi(x))\) は図2の式(7)のように調和ポテンシャル型になっており、レプリカごとに異なる反応座標 \(\xi_{i}\)に系を拘束するようになっている。\(\xi_{i}\)を定期的に交換することで、エネルギー障壁にとらわれず、反応座標空間を広く探索できる。
本計算用のインプットファイルでは、[GAMD] に 3. で決定した GaMD のパラメータを入力する(図8)。GaMD のパラメータを固定するために、update_period は 0 にしておく。REUS も同時に行うので、[REMD] に REUS の設定を入力する。dimension はレプリカ交換のパラメータの次元で、ここでは 1 とする。exchange_period は交換の頻度で、ここでは1000ステップに一度 REUS のパラメータを交換する。REUS の場合は type1 を RESTRAINT にする。nreplica1 はレプリカの数である。rest_function1 では REUS で用いるバイアスポテンシャルとして、[RESTRAINTS] の拘束ポテンシャルの番号を指定する。[OUTPUT] で GaREUS で出力されるファイルを指定する。remfile は各レプリカにおけるパラメータ番号が出力され、計算結果をソーティングする際に利用する。
REUS で用いるバイアスポテンシャルは図9のように指定する。まず、[SELECTION] でバイアスをかける原子を指定する。ここでは図1の点線赤丸が囲った酸素原子と水素原子をそれぞれ group1, group2 で指定している。[RESTRAINTS] ではバイアスの関数を指定する。function が DIST とし、select_index を 1 2 とすると、[SELECTION] で指定した group1 と group2 の原子間に距離の拘束ポテンシャルがかかる。調和ポテンシャルの係数と平衡値は、constant と reference で指定する。REUS で用いるレプリカ数に対応した数の値を指定する。図9のように reference の値をレプリカごとに変えることで、反応座標上のそれぞれの場所に拘束がかかることになる。
以上のインプットファイルを基に GENESIS で本計算を実行する。ログファイルに [REMD] の exchange_period で指定したステップごとにレプリカの交換に関する情報が出力される(図10)。この例では 4 と 5 が交換しており、AcceptanceRatio が 1 増えている。交換後のパラメータの番号とレプリカの番号(トラジェクトリーの番号)との対応は RepIDtoParmID と ParmIDtoRepID からわかる。[RESTRAINTS] で指定した反応座標のパラメータによっては交換率が低すぎたり、高すぎたりすることがあるが、その場合はパラメータを再調節する。全レプリカで AcceptanceRatio が均一に20~30%程度になるようにパラメータを選択するのが良いとされている。
5. 解析
GaREUS 法で得られたトラジェクトリーには GaMD のバイアス \(\Delta U^{\mathrm{GaMD}}(U(x))\) と REUS のバイアス \(\Delta U_{i}^{\mathrm{REUS}} (\xi(x))\) がかかっている。トラジェクトリーから直接自由エネルギー地形を計算してしまうと、これらのバイアスがかかった不正確な地形が得られてしまう。正確な自由エネルギー地形を得るために、GaREUS のトラジェクトリーの確率分布を Reweighting することでバイアスを取り除く必要がある。ここでは二段階の Reweighting を行う。まず REUS のバイアスを取り除き、続いて GaMD のバイアスを取り除く。
本計算で得られた各レプリカのトラジェクトリーでは、REUS のパラメータ交換によって1つのレプリカ内でバイアスのパラメータが時間によって変化している。つまり、トラジェクトリー内の各スナップショットには異なるバイアスがかかっている。REUS のバイアスの効果を取り除くにはバイアスパラメータごとにスナップショットがまとめられている方が扱いやすいので、まずトラジェクトリーをパラメータごとにソーティング。GENESIS の remd_convert に図11のようなインプットを入力し、ソーティングする。[INPUT] の dcdfile, remfile, logfile にそれぞれ GaREUS で得た各レプリカのトラジェクトリー(dcd ファイル)、remfile、logfile を指定し、[OPTION] にステップ数や exchange_period 等の対応する値を指定する。ソーティングされたファイルは [OUTPUT] で指定した trjfile や logfile に出力される。出力された dcd ファイル内では、1つのバイアスパラメータのみが用いられている(例えば par1.dcd では1番目のパラメータのみ)。
ソーティングされたトラジェクトリーから反応座標の値を計算する。図12のようなインプットファイルを GENESIS の trj_analysis に入力する。[TRAJECTORY] の trjfile に先ほどソーティングして得た dcd ファイルを指定し、md_step, mdout_period に GaREUS で用いた MD のステップ数と出力頻度を指定する。2原子間の距離の場合は [OPTION] に distance を指定すると、トラジェクトリーから距離を計算し、[OUTPUT] の disfile で指定したファイルに出力される。二面角を使う場合は distance の代わりに torsion、角度の場合は angle とし、[OUTPUT] ではそれぞれ disfile の代わりに torfile, angfile でファイルを指定する。すべてのトラジェクトリー(つまりすべてのレプリカの dcd ファイル)に対して同様の計算を行う。
MultiState Bennett Acceptance Ratio(MBAR)を用いて、REUS のバイアスを取り除く(文献10)。図13のようなインプットファイルを GENESIS の mbar_analysis に入力する。反応座標の結果を [INPUT] の cvfile に指定し、[RESTRAINTS] に REUS で用いた調和ポテンシャルバイアスのパラメータを指定する。[OUTPUT] で weightfile, fenefile, pmffile を指定すると、それぞ重み、レプリカ間の自由エネルギー変化、反応座標に沿った自由エネルギー地形(PMF)を出力できる。[MBAR] で MBAR の設定を指定する。temperature は計算で用いた温度にし、rest_funciton で [RESTRAINTS] の関数を指定する。grids で PMF のグリッドを指定でき、0.0 15.0 301 とすると、反応座標が 0.0 から 15.0 の範囲で等間隔で301個のグリッドごとに PMF を出力する。mbar_analysis で特に重要なものは、weightfile で出力される重みで、これは GaREUS で得た各スナップショットごとの確率に対応している。この重みを用いることで、GaREUS で指定していない反応座標空間にも射影することで、REUS のバイアスがかかてっていない自由エネルギー地形を求めることができる。ただ、mbar_analysis で取り除けるバイアスは REUS のもののみで、GaMD のバイアスは取り除けていない。
最後に、GaMD のバイアスを取り除く。バイアスがかかっていない確率分布 \(p(\xi)\) は図2の式(8)のように変形できる。ここでダッシュ記号がついているものは GaMD のバイアスがかかった分布や平均値である。MBAR によって REUS のバイアスは取り除かれているので、mbar_analysis で得られた重みから\(p’(\xi)\) は計算できる。\(\exp[\beta \Delta U^{\mathrm{GaMD}}]\) の平均は統計的に収束が非常に悪く、そのまま計算すると誤差が非常に大きくなる。そのため、この項はキュムラント展開をし、二次の項までで近似する(文献11)。これは \(\Delta U^{\mathrm{GaMD}}\) の分布を正規分布(Gaussian)で近似していることに対応する。ソーティングした logfile に出力されている GaMD のブーストポテンシャル \(\Delta U^{\mathrm{GaMD}}\) と mbar_analysis で得た重みから、\(p(\xi)\) を計算する。現在 GENESIS の Analysis Tools には GaMD バイアスの Reweighting 用のプログラムは用意されていない。今後 GENESIS のウェブサイトで公開予定の GaREUS のチュートリアルで Reweighting 用の Python スクリプトを配布する予定である。
図14は反応座標に沿った自由エネルギー地形の結果である。GaMD のバイアスがかかったもの(つまり MBAR で REUS のバイアスだけ取り除いたもの)ではエネルギー障壁が低いが、全バイアスを取り除いたもの(Unbiased)ではエネルギー障壁が高くなっている。GaMD によって小さくなった障壁が Reweighting によって正しく戻されていることがわかる。
\(p(\xi)\) での反応座標 \(\xi\) は、GaREUS で用いた反応座標と同じである必要はなく、任意の反応座標に対して計算することができ、複数の反応座標にも対応している。例えば、Alanine Tripeptide の2つの二面角 φ(Ala1C-Ala2N-Ala2Cα-Ala2C)と ψ(Ala2N-Ala2Cα-Ala2C-Ala3N)を用いて二次元の自由エネルギー地形を計算すると図15のようになる。GaMD のバイアスがかかっている状態(GaMD biased)だと全体的に浅い地形になっており、ベイスン間を移動しやすくなっている。バイアスを取り除いた地形(Unbiased)はエネルギー障壁が元通りに高くなっている。このように GaMD のバイアスをかけることで、REUS で用いた反応座標以外の自由度に対しても動きやすくなっており、広く構造探索ができるようになり、Reweighting によって正しい自由エネルギー地形に戻すことができる。
以上が GaREUS による自由エネルギー計算のプロトコルであり、通常の REUS シミュレーションと比較して効率的に自由エネルギー地形を求めることができる。計算時間は系に含まれる原子数に大きく依存するため、一概に目安は述べることは難しい。対象とする系で通常の MD 計算を行い、計算時間を見積もってから GPU クラスターやスーパーコンピュータで計算することをお勧めする。また、GaREUS 法で用いた入力パラメータ等の詳細や一覧については、GENESIS のマニュアルにまとめられているので、そちらを参照してほしい。
文献
- Miao, Y. et al., J. Chem. Theory Comput., 11, 3584–3595 (2015)
- Pang, Y. T. et al., J. Chem. Theory Comput., 13, 9–19 (2017)
- Sugita, Y. et al., J. Chem. Phys., 113, 6042–6051 (2000)
- Fukunishi, H. et al., J. Chem. Phys., 116, 9058–9067 (2002)
- Oshima, H. et al., J. Chem. Theory Comput., 15, 5199–5208 (2019)
- Jung, J. et al., Wiley Interdiscip. Rev. Comput.Mol. Sci., 5, 310−323 (2015)
- Kobayashi, C. et al., J. Comput. Chem., 38, 2193–2206 (2017)
- 小林千草, 蛋白質科学会アーカイブ, 11, e091 (2018)
- Hamelberg, D. et al., J. Chem. Phys., 120, 11919–11929 (2004)
- Shirts, M. R. & Chodera, J. D., J. Chem. Phys., 129, 124105 (2008)
- Miao, Y. et al., J. Chem. Theory Comput., 10, 2677–2689 (2014)
-
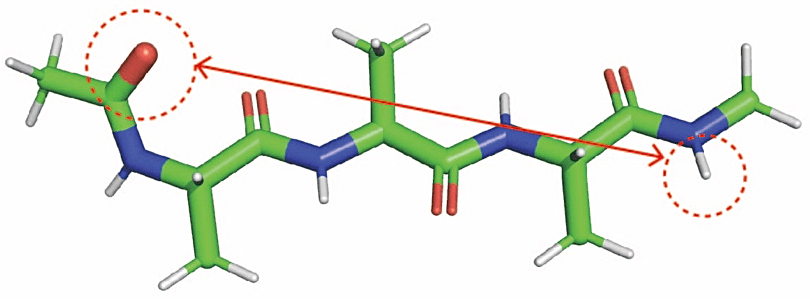
図1:Alanine Tripeptide。点線丸で囲った原子間の距離を反応座標として使用。 -
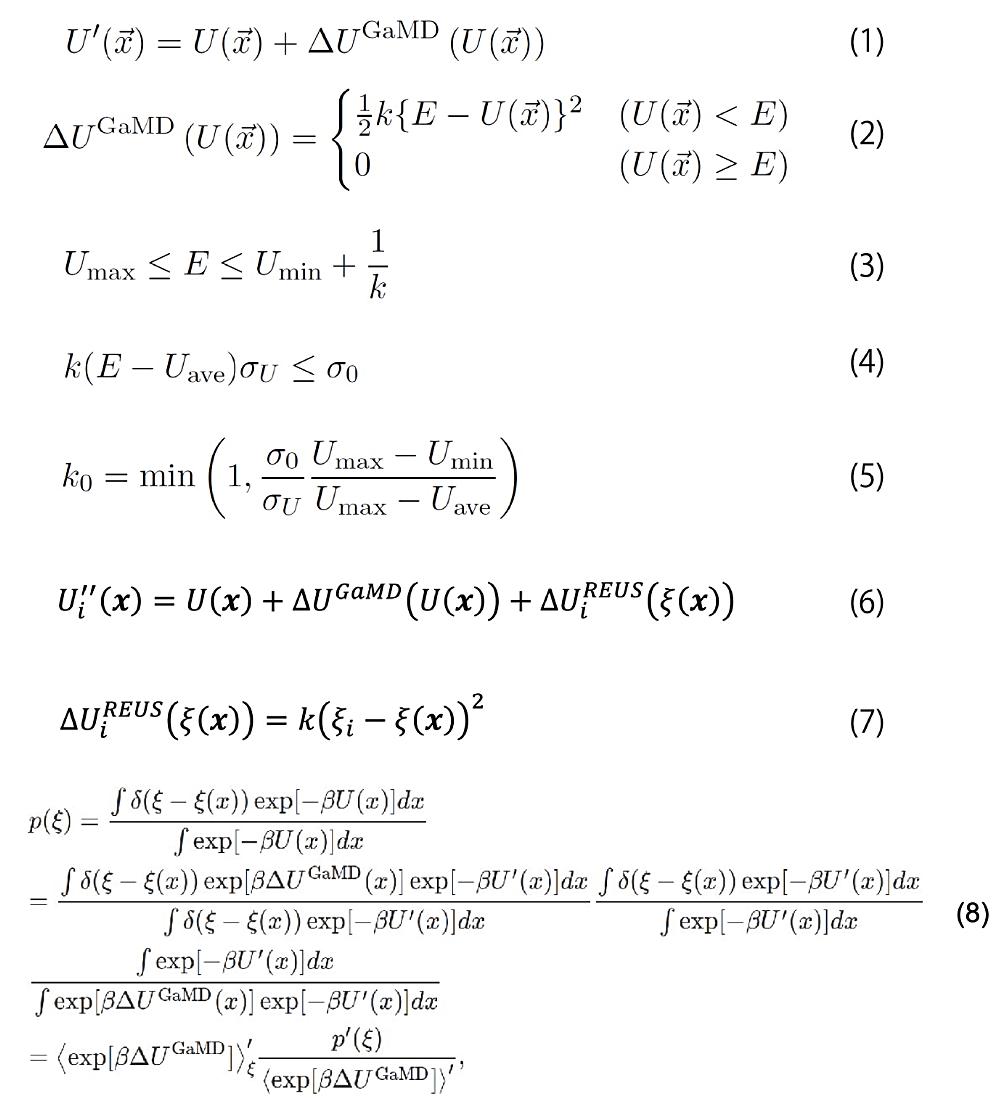
図2:GaREUS で用いる数式。 -
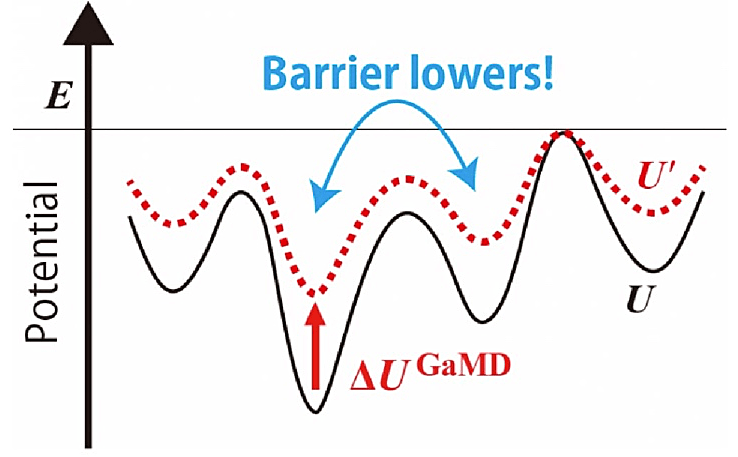
図3:GaMD のイメージ図。ブーストポテンシャルによってエネルギー障壁が下がる。 -
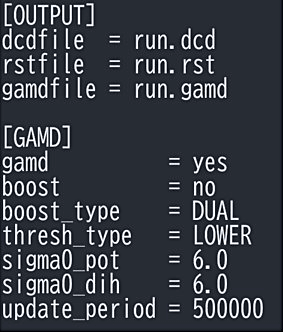
図4:初期パラメータ設定のための GaMD のインプットファイルの一部。 -

図5:GaMD の初期パラメータの出力の例 -
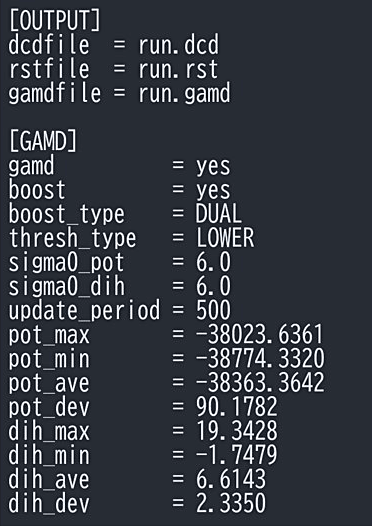
図6:パラメータを更新するための GaMD インプットファイルの一部。 -

図7:GaMD のパラメータの更新の例 -
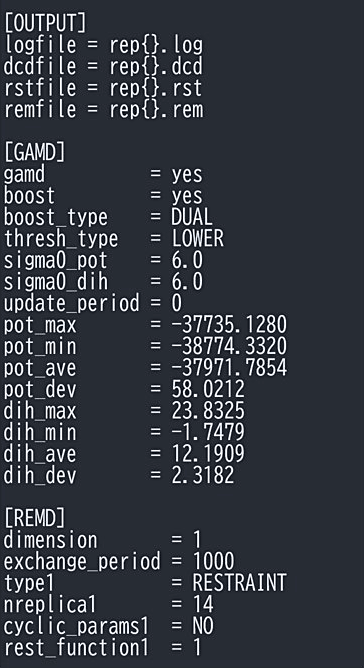
図8:GaREUS のインプットファイルの一部。 -
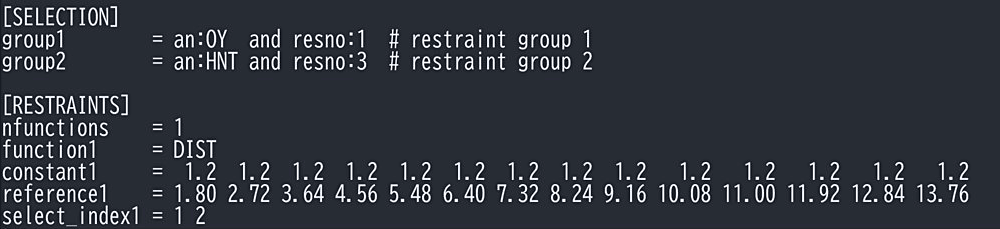
図9:GaREUS で指定する反応座標パラメータ例。 -
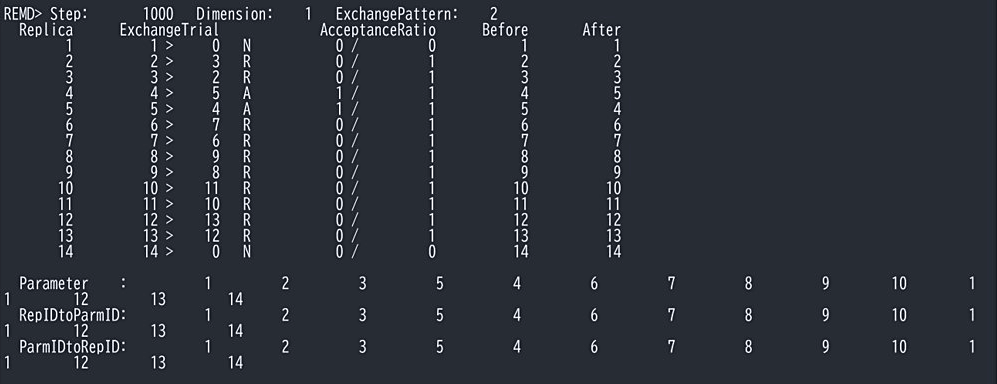
図10:GaREUS のログファイルの例。レプリカ交換の結果が出力されている。 -
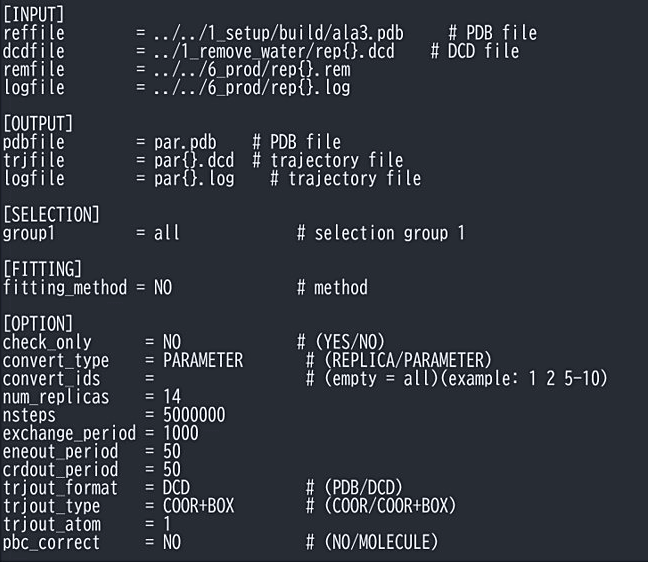
図11: remd_convertのインプット例。 -
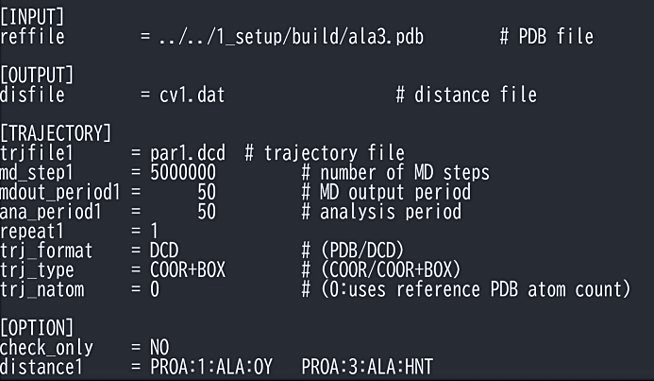
図12: trj_analysisのインプット例。 -
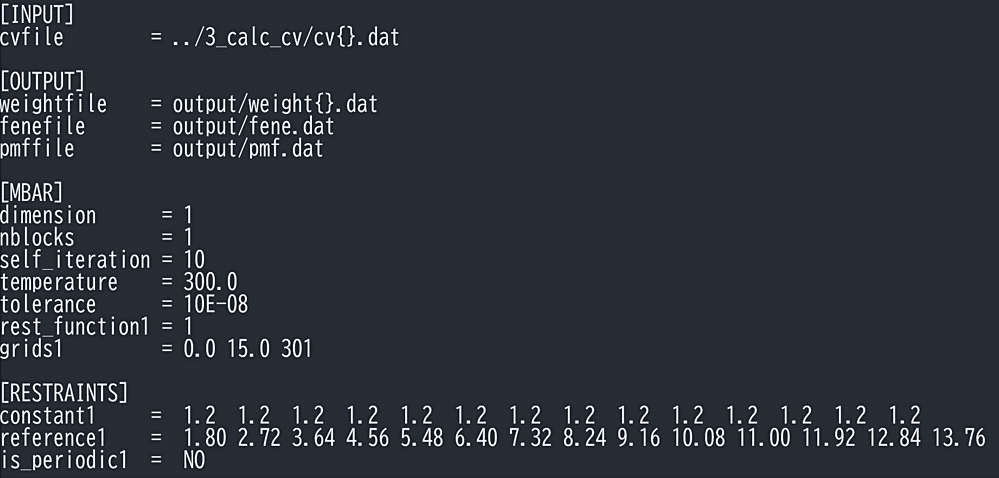
図13: mbar_analysisのインプット例。 -
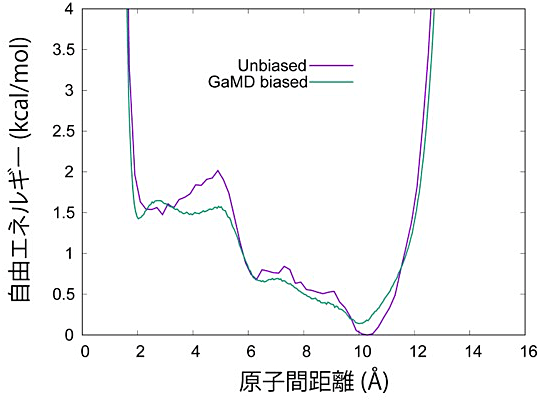
図14:GaREUS で用いた反応座標の自由エネルギー地形 GaMD のバイアスがかかったもの(GaMD biased)とバイアスを取り除いたもの(Unbiased)。 -
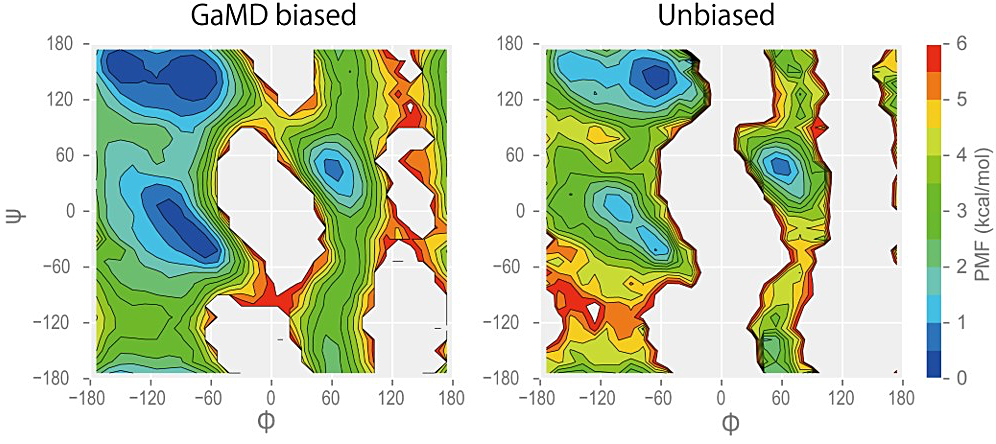
図15:GaREUS で用いていない反応座標(二面角 φ と ψ)の自由エネルギー地形 GaMD のバイアスがかかったもの(GaMD biased)とバイアスを取り除いたもの(Unbiased)。
イントロダクション
分子動力学シミュレーション(Molecular Dynamics: MD)は、粒子間に働く相互作用および力を計算し、運動方程式を解くことで、粒子の運動を求める方法である。溶媒を含む全ての相互作用を考慮し、古典力学の範囲内で生体分子の動的構造を計算し、その計算結果を解析することで様々な物理量を求めることができる。タンパク質や核酸などの生体分子の動的構造や相互作用を原子解像度で調べる手法として生命科学において広く用いられている。特に、MD シミュレーションでは各状態での安定性または存在確率を求めることができ、これらは自由エネルギー地形と呼ばれている。自由エネルギー地形を詳細に分析することで、生体分子の構造変化や分子機構を理解することができる。
しかし、生体分子の自由エネルギー地形は多数の局所安定状態を持った複雑な形状をしており、限られた計算時間ではシミュレーションが局所安定状態に捕らわれてしまう。この問題を避けるために、拡張アンサンブル法などの効率的なサンプリング法が用いられている。拡張アンサンブル法では、エネルギーあるいは事前に定義された反応座標における一次元ランダムウォークを実現することで、状態空間を広く探索する。
様々な拡張アンサンブル法が提案されているが、計算コストを抑えつつ、タンパク質構造を効率的に探索する計算手法が望ましい。そのような計算手法として、我々は Gaussian accelerated MD(GaMD)法(文献1,2)と Replica-Exchange Umbrella Sampling(REUS)法(文献3,4)の2つの拡張アンサンブル法を組み合わせた Gaussian accelerated Replica-Exchange Umbrella Sampling(GaREUS)法を提案した(文献5)。GaREUS 法では、GaMD 法によってタンパク質の構造柔軟性を向上させ、同時に REUS 法によって反応座標空間を広く探索する。GaREUS 法で得られたトラジェクトリーから二段階の Reweighting を行うことで、正確な自由エネルギー地形を求めることが出来る。GaREUS 法は、理化学研究所で開発している MD シミュレーションソフトウェア「GENESIS」(文献6,7)に実装されており,GPU ワークステーションからスーパーコンピュータまで様々な計算機を用いた計算が可能である。本稿では GaREUS 法を用いた自由エネルギー地形の計算方法を説明する。
計算機・ソフトウェア
GaREUS 法の実行には MD シミュレーションソフトウェア GENESIS を用いる。GENESIS はオープンソフトウェア(LGPLv3)として公開しており、無料で利用できる。最新版は GENESIS のウェブサイトから入手可能である。
GENESIS をコンパイル・実行するには、OS として Linux、C コンパイラおよび Fortran コンパイラとして gcc、gfortran または Intel Fortran/C++ compiler、開発環境として GNU autoconf、並列計算ライブラリーとして OpenMPI、数学ライブラリーとして BLAS と LAPACK が必要である。GPU を利用する場合は CUDA ライブラリーも必要となる。詳細な必要条件やコンパイル方法は GENESIS のウェブサイトかマニュアルを参考にしてほしい。
GaREUS 法では複数のレプリカ(MD シミュレーション)を同時に実行する必要があるため、複数の計算ノードを持ったコンピュータクラスターかスーパーコンピュータを用いる。Intel 社、AMD 社、富士通(A64FX)の CPU を搭載しており、GPU を利用する場合は、CUDA 対応の nVIDIA 社の GPU を搭載したものを用いる。例えば、10レプリカの計算をする場合、8CPU コア以上を搭載した計算ノードが10個必要となる。複数ノードを用いた計算にはバッチジョブシステムの利用が必要だが、利用方法はソフトウェアや計算機システムごとに大きく異なるため、各システムのマニュアルを参照するか管理者に問い合わせてほしい。
計算手順
- 生体分子モデルのセットアップ
- 構造最適化と平衡化
- GaMD パラメータの決定
- 本計算
- 解析
実験の詳細
1. 生体分子モデルのセットアップ
例として Alanine Tripeptide を用いる(図1)。GaREUS の反応座標として、残基1の酸素と残基3の水素の原子間距離を用いる(図1の点線丸)。Alanine Tripeptide に水分子を加え、一辺 50 Å 程度のボックスを作る。ここでは力場パラメータとして CHARMM 力場の C36 を用いる。タンパク質のセットアップについては、GENESIS のウェブサイトのチュートリアル(Level 1: Basic tutorials)および文献8で説明されているので、そちらを参照していただきたい。
2. 構造最適化と平衡化
セットアップで得た構造は原子同士が衝突していたり、不安定な構造になっていたりすることがある。ポテンシャルエネルギーが極端に高すぎるため、そのまま MD 計算をしてしまうとシステムが崩壊してしまう。構造最適化によってポテンシャルエネルギーを下げ、原子の衝突を取り除く。このとき、対象としているタンパク質やリガンドの位置や距離に拘束をかけ、分子が動かないようにする。GENESIS では最急降下法で構造最適化を行う。
構造最適化が終わったシステムは分子に速度が与えられていない絶対零度の状態になっている。分子に初期速度を与え、システムの温度を標的温度までゆっくりと上昇させる。GENESIS では Langevin 熱浴で等温等積(NVT)の MD 計算を行う。
次に、等温等圧(NPT)で MD 計算を行い、システムの体積を調整する。体積の時間変化を確認し、体積があまり変化しなくなるまでシミュレーションを行う。GENESIS では Bussi の方法で温度・圧力を調整する。
最後に、本計算と同じ熱力学条件で平衡化を行う。平衡化に必要なステップ数はシステムによって異なるため、温度、体積、ポテンシャルエネルギーの時間変化がドリフトしていないか注意する。構造のトラジェクトリーを見て、構造が壊れていないかも確認する。Root-Mean-Square Displacement(RMSD)や Root-Mean-Square Fluctuation(RMSF)等で時間変化を確認し、あまり変化しなくなったところで平衡化を終える。構造最適化および平衡化についても GENESIS のウェブサイトのチュートリアル(Level 1: Basic tutorials)および文献8で GENESIS のインプットファイルも含めて詳細な説明されているので、そちらを参照していただきたい。
3. GaMD パラメータの決定
GaMD ではシステムの本来のポテンシャル \(U(x)\) にバイアス \(\Delta U^{\mathrm{GaMD}}(U(x))\) を加えることで、エネルギー障壁を下げる(図2の式(1)および図3)。\(U(x)\) が閾値 \(E\) よりも小さいときのみ調和ポテンシャル型のバイアスを加え、それ以外は何も足さない(図2の式(2))。このようにすることで、システムを局所安定な状態に捉えられることなく、状態空間を広くサンプリングすることができるようになる。\(U’(x)\) が連続関数かつ \(U(x)\) における大小関係(\(U(x_{1}) < U(x_{2})\) ならば \(U’(x_{1}) < U’(x_{2})\))を維持するために、閾値 \(E\) はポテンシャルの最大値 \(U_{\mathrm{max}}\) と最小値 \(U_{\mathrm{min}}\) によって条件づけられる(図2の式(3))。また、正確な Reweighting のために、\(U’(x)\) の分散は図2の式(4)を満たす必要がある。ここで、\(U_{\mathrm{ave}}\) と \(\sigma_{U}\) はそれぞれポテンシャルの \(U(x)\) の平均値と分散で、\(\sigma_{0}\) はユーザーが設定する分散の最大値である。\(k_{0}\) を \(k(U_{\mathrm{max}} - U_{\mathrm{min}})\) と定義すると、閾値 \(E\) を下限 \(U_{\mathrm{max}}\) に設定する場合、\(k_{0}\) は図2の式(5)で決定する。ここでは最小限の説明しかしていないが、GaMD のパラメータの詳細は Miao の原著論文(文献1,2)を参照していただきたい。
GaMD では二面角とそれ以外の全ポテンシャルエネルギーを別々にブーストする「デュアルブースト」が利用できる(文献9)。二面角のブーストによってタンパク質の構造柔軟性を向上し、構造探索を加速する。同時に、二面角以外の全ポテンシャルエネルギーをブーストすることで、タンパク質近傍の水分子の運動等を加速し、ケージング効果等を回避する。デュアルブーストの場合は、上記の GaMD パラメータが二面角とそれ以外の全ポテンシャルエネルギーに対してそれぞれ必要となる。
\(k\) と \(E\) を決めるには \(U_{\mathrm{max}}\), \(U_{\mathrm{min}}\), \(U_{\mathrm{ave}}\), \(\sigma_{U}\) が必要となるが、系のポテンシャルエネルギー地形が複雑なため、一般的にはこれらは事前にわからない。まずブーストをかけずに MD 計算を行い、ポテンシャルの形状を探索し、これらのパラメータを決める。通常の MD のインプットに加えて、[GAMD] セクションを追加する(図4)。それぞれのパラメータの意味は、gamd は GaMD をするか否か、boost=no はブーストしない、boost_type=DUAL はデュアルブーストを用いる、thresh_type=LOWER は式(3)の下限 \(E_{\mathrm{max}}\) を用いる、sigma0_dih と sigma0_pot はそれぞれ二面角とそれ以外のポテンシャルの \(\sigma_{0}\) という意味である。update_period は GaMD のパラメータ \(U_{\mathrm{max}}\), \(U_{\mathrm{min}}\), \(U_{\mathrm{ave}}\), \(\sigma_{U}\) を更新する頻度で、この段階では MD 計算のステップ数を同じにしておく。
計算が終わると [OUTPUT] の gamdfile で指定したファイルに図5のような結果が出力される。POT_MAX, POT_MIN, POT_AVE, POT_DEV が二面角以外のポテンシャルの \(U_{\mathrm{max}}\), \(U_{\mathrm{min}}\), \(U_{\mathrm{ave}}\), \(\sigma_{U}\) であり、POT_TH, POT_KC, POT_KC0 はそれらから計算した \(E\) と \(k\) となっている。同様に DIH が付いたものは二面角のパラメータである。
初期パラメータが決まったら、実際に GaMD のブーストポテンシャルを加えながらパラメータを更新していく。[GAMD] で boost=yes とし、pot_max や dih_max 等に先ほどの gamdfile に出力された初期パラメータを入力する(図6)。ブーストポテンシャルを加えることで探索できるポテンシャル表面の領域が広がり、\(U_{\mathrm{max}}\), \(U_{\mathrm{min}}\), \(U_{\mathrm{ave}}\), \(\sigma_{U}\) が変化する。update_period=500 とすると500ステップごとに、pot_max や dih_max 等を新たな \(U_{\mathrm{max}}\), \(U_{\mathrm{min}}\), \(U_{\mathrm{ave}}\), \(\sigma_{U}\) を基に更新する。パラメータの更新を繰り返すことで、探索できるポテンシャル表面が徐々に広くなっていき、より良い \(U_{\mathrm{max}}\), \(U_{\mathrm{min}}\), \(U_{\mathrm{ave}}\), \(\sigma_{U}\) が見つかりやすくなる。
更新されたパラメータは update_period ごとに gamdfile で指定されたファイルに出力される(図7)。パラメータの時間変化を確認し、あまり変化しなくなったところで計算を終える。出力の最後の行の値で GaMD のパラメータを決定し、以降は変化させない。
4. 本計算
GaREUS では、GaMD のブーストポテンシャル \(\Delta U^{\mathrm{GaMD}}(U(x))\) を加えつつ、REUS シミュレーションを行う(図2の式(6))。\(\Delta U_{i}^{\mathrm{REUS}} (\xi(x))\) は REUS のバイアスポテンシャル、\(\xi(x)\) は REUS で用いる反応座標、\(i\) はレプリカの番号である。\(\Delta U_{i}^{\mathrm{REUS}} (\xi(x))\) は図2の式(7)のように調和ポテンシャル型になっており、レプリカごとに異なる反応座標 \(\xi_{i}\)に系を拘束するようになっている。\(\xi_{i}\)を定期的に交換することで、エネルギー障壁にとらわれず、反応座標空間を広く探索できる。
本計算用のインプットファイルでは、[GAMD] に 3. で決定した GaMD のパラメータを入力する(図8)。GaMD のパラメータを固定するために、update_period は 0 にしておく。REUS も同時に行うので、[REMD] に REUS の設定を入力する。dimension はレプリカ交換のパラメータの次元で、ここでは 1 とする。exchange_period は交換の頻度で、ここでは1000ステップに一度 REUS のパラメータを交換する。REUS の場合は type1 を RESTRAINT にする。nreplica1 はレプリカの数である。rest_function1 では REUS で用いるバイアスポテンシャルとして、[RESTRAINTS] の拘束ポテンシャルの番号を指定する。[OUTPUT] で GaREUS で出力されるファイルを指定する。remfile は各レプリカにおけるパラメータ番号が出力され、計算結果をソーティングする際に利用する。
REUS で用いるバイアスポテンシャルは図9のように指定する。まず、[SELECTION] でバイアスをかける原子を指定する。ここでは図1の点線赤丸が囲った酸素原子と水素原子をそれぞれ group1, group2 で指定している。[RESTRAINTS] ではバイアスの関数を指定する。function が DIST とし、select_index を 1 2 とすると、[SELECTION] で指定した group1 と group2 の原子間に距離の拘束ポテンシャルがかかる。調和ポテンシャルの係数と平衡値は、constant と reference で指定する。REUS で用いるレプリカ数に対応した数の値を指定する。図9のように reference の値をレプリカごとに変えることで、反応座標上のそれぞれの場所に拘束がかかることになる。
以上のインプットファイルを基に GENESIS で本計算を実行する。ログファイルに [REMD] の exchange_period で指定したステップごとにレプリカの交換に関する情報が出力される(図10)。この例では 4 と 5 が交換しており、AcceptanceRatio が 1 増えている。交換後のパラメータの番号とレプリカの番号(トラジェクトリーの番号)との対応は RepIDtoParmID と ParmIDtoRepID からわかる。[RESTRAINTS] で指定した反応座標のパラメータによっては交換率が低すぎたり、高すぎたりすることがあるが、その場合はパラメータを再調節する。全レプリカで AcceptanceRatio が均一に20~30%程度になるようにパラメータを選択するのが良いとされている。
5. 解析
GaREUS 法で得られたトラジェクトリーには GaMD のバイアス \(\Delta U^{\mathrm{GaMD}}(U(x))\) と REUS のバイアス \(\Delta U_{i}^{\mathrm{REUS}} (\xi(x))\) がかかっている。トラジェクトリーから直接自由エネルギー地形を計算してしまうと、これらのバイアスがかかった不正確な地形が得られてしまう。正確な自由エネルギー地形を得るために、GaREUS のトラジェクトリーの確率分布を Reweighting することでバイアスを取り除く必要がある。ここでは二段階の Reweighting を行う。まず REUS のバイアスを取り除き、続いて GaMD のバイアスを取り除く。
本計算で得られた各レプリカのトラジェクトリーでは、REUS のパラメータ交換によって1つのレプリカ内でバイアスのパラメータが時間によって変化している。つまり、トラジェクトリー内の各スナップショットには異なるバイアスがかかっている。REUS のバイアスの効果を取り除くにはバイアスパラメータごとにスナップショットがまとめられている方が扱いやすいので、まずトラジェクトリーをパラメータごとにソーティング。GENESIS の remd_convert に図11のようなインプットを入力し、ソーティングする。[INPUT] の dcdfile, remfile, logfile にそれぞれ GaREUS で得た各レプリカのトラジェクトリー(dcd ファイル)、remfile、logfile を指定し、[OPTION] にステップ数や exchange_period 等の対応する値を指定する。ソーティングされたファイルは [OUTPUT] で指定した trjfile や logfile に出力される。出力された dcd ファイル内では、1つのバイアスパラメータのみが用いられている(例えば par1.dcd では1番目のパラメータのみ)。
ソーティングされたトラジェクトリーから反応座標の値を計算する。図12のようなインプットファイルを GENESIS の trj_analysis に入力する。[TRAJECTORY] の trjfile に先ほどソーティングして得た dcd ファイルを指定し、md_step, mdout_period に GaREUS で用いた MD のステップ数と出力頻度を指定する。2原子間の距離の場合は [OPTION] に distance を指定すると、トラジェクトリーから距離を計算し、[OUTPUT] の disfile で指定したファイルに出力される。二面角を使う場合は distance の代わりに torsion、角度の場合は angle とし、[OUTPUT] ではそれぞれ disfile の代わりに torfile, angfile でファイルを指定する。すべてのトラジェクトリー(つまりすべてのレプリカの dcd ファイル)に対して同様の計算を行う。
MultiState Bennett Acceptance Ratio(MBAR)を用いて、REUS のバイアスを取り除く(文献10)。図13のようなインプットファイルを GENESIS の mbar_analysis に入力する。反応座標の結果を [INPUT] の cvfile に指定し、[RESTRAINTS] に REUS で用いた調和ポテンシャルバイアスのパラメータを指定する。[OUTPUT] で weightfile, fenefile, pmffile を指定すると、それぞ重み、レプリカ間の自由エネルギー変化、反応座標に沿った自由エネルギー地形(PMF)を出力できる。[MBAR] で MBAR の設定を指定する。temperature は計算で用いた温度にし、rest_funciton で [RESTRAINTS] の関数を指定する。grids で PMF のグリッドを指定でき、0.0 15.0 301 とすると、反応座標が 0.0 から 15.0 の範囲で等間隔で301個のグリッドごとに PMF を出力する。mbar_analysis で特に重要なものは、weightfile で出力される重みで、これは GaREUS で得た各スナップショットごとの確率に対応している。この重みを用いることで、GaREUS で指定していない反応座標空間にも射影することで、REUS のバイアスがかかてっていない自由エネルギー地形を求めることができる。ただ、mbar_analysis で取り除けるバイアスは REUS のもののみで、GaMD のバイアスは取り除けていない。
最後に、GaMD のバイアスを取り除く。バイアスがかかっていない確率分布 \(p(\xi)\) は図2の式(8)のように変形できる。ここでダッシュ記号がついているものは GaMD のバイアスがかかった分布や平均値である。MBAR によって REUS のバイアスは取り除かれているので、mbar_analysis で得られた重みから\(p’(\xi)\) は計算できる。\(\exp[\beta \Delta U^{\mathrm{GaMD}}]\) の平均は統計的に収束が非常に悪く、そのまま計算すると誤差が非常に大きくなる。そのため、この項はキュムラント展開をし、二次の項までで近似する(文献11)。これは \(\Delta U^{\mathrm{GaMD}}\) の分布を正規分布(Gaussian)で近似していることに対応する。ソーティングした logfile に出力されている GaMD のブーストポテンシャル \(\Delta U^{\mathrm{GaMD}}\) と mbar_analysis で得た重みから、\(p(\xi)\) を計算する。現在 GENESIS の Analysis Tools には GaMD バイアスの Reweighting 用のプログラムは用意されていない。今後 GENESIS のウェブサイトで公開予定の GaREUS のチュートリアルで Reweighting 用の Python スクリプトを配布する予定である。
図14は反応座標に沿った自由エネルギー地形の結果である。GaMD のバイアスがかかったもの(つまり MBAR で REUS のバイアスだけ取り除いたもの)ではエネルギー障壁が低いが、全バイアスを取り除いたもの(Unbiased)ではエネルギー障壁が高くなっている。GaMD によって小さくなった障壁が Reweighting によって正しく戻されていることがわかる。
\(p(\xi)\) での反応座標 \(\xi\) は、GaREUS で用いた反応座標と同じである必要はなく、任意の反応座標に対して計算することができ、複数の反応座標にも対応している。例えば、Alanine Tripeptide の2つの二面角 φ(Ala1C-Ala2N-Ala2Cα-Ala2C)と ψ(Ala2N-Ala2Cα-Ala2C-Ala3N)を用いて二次元の自由エネルギー地形を計算すると図15のようになる。GaMD のバイアスがかかっている状態(GaMD biased)だと全体的に浅い地形になっており、ベイスン間を移動しやすくなっている。バイアスを取り除いた地形(Unbiased)はエネルギー障壁が元通りに高くなっている。このように GaMD のバイアスをかけることで、REUS で用いた反応座標以外の自由度に対しても動きやすくなっており、広く構造探索ができるようになり、Reweighting によって正しい自由エネルギー地形に戻すことができる。
以上が GaREUS による自由エネルギー計算のプロトコルであり、通常の REUS シミュレーションと比較して効率的に自由エネルギー地形を求めることができる。計算時間は系に含まれる原子数に大きく依存するため、一概に目安は述べることは難しい。対象とする系で通常の MD 計算を行い、計算時間を見積もってから GPU クラスターやスーパーコンピュータで計算することをお勧めする。また、GaREUS 法で用いた入力パラメータ等の詳細や一覧については、GENESIS のマニュアルにまとめられているので、そちらを参照してほしい。
文献
- Miao, Y. et al., J. Chem. Theory Comput., 11, 3584–3595 (2015)
- Pang, Y. T. et al., J. Chem. Theory Comput., 13, 9–19 (2017)
- Sugita, Y. et al., J. Chem. Phys., 113, 6042–6051 (2000)
- Fukunishi, H. et al., J. Chem. Phys., 116, 9058–9067 (2002)
- Oshima, H. et al., J. Chem. Theory Comput., 15, 5199–5208 (2019)
- Jung, J. et al., Wiley Interdiscip. Rev. Comput.Mol. Sci., 5, 310−323 (2015)
- Kobayashi, C. et al., J. Comput. Chem., 38, 2193–2206 (2017)
- 小林千草, 蛋白質科学会アーカイブ, 11, e091 (2018)
- Hamelberg, D. et al., J. Chem. Phys., 120, 11919–11929 (2004)
- Shirts, M. R. & Chodera, J. D., J. Chem. Phys., 129, 124105 (2008)
- Miao, Y. et al., J. Chem. Theory Comput., 10, 2677–2689 (2014)


